阿羅的不可能定理

出自 MBA智库百科(https://wiki.mbalib.com/)

阿羅的不可能定理（Arrow's Impossibility Theorem）

　　阿羅不可能定理是由1972年諾貝爾經濟學獎的獲得者之一阿羅首先陳述和證明的。

　　1951年肯尼斯·約瑟夫·阿羅（Kenneth J．Arrow)在他的現在已經成為經濟學經典著作的《社會選擇與個人價值》一書中，採用數學的公理化方法對通行的投票選舉方式能否保證產生出合乎大多數人意願的領導者或者說“將每個個體表達的先後次序綜合成整個群體的偏好次序”進行了研究。結果，他得出了一個驚人的結論：絕大多數情況下是——不可能的！更準確的表達則是：當至少有三名候選人和兩位選民時，不存在滿足阿羅公理的選舉規則。或者也可以說是：隨著候選人和選民的增加，“程式民主”必將越來越遠離“實質民主”。

　　定理前提：假設有一個非常民主的群體，或者說是一個希望在民主基礎上作出自己的所有決策的社會，對它來說，群體中每一個成員的要求都是同等重要的。一般地，對於最應該做的事情，群體的每一個成員都有自己的偏好。為了決策，就要建立一個公正而一致的程式，能把個體的偏好結合起來，達成某種共識。這就要進一步假設群體中的每一個成員都能夠按自己的偏好對所需要的各種選擇進行排序，對所有這些排序的匯聚就是群體的排序。

　　阿羅不可能定理的證明並不難，但是需要嚴格的數學邏輯思維。關於這個定理還有一段情節頗為曲折的故事。

　　阿羅在大學期間就迷上了數學邏輯：讀四年級的時候， 波蘭大邏輯學家塔斯基(Tarski) 到阿羅所在的大學講了一年的關係演算， 阿羅在他那裡接觸到諸如傳遞性、排序等概念 在此之前． 阿羅對他所著迷的邏輯學還是全靠自學呢。

　　後來， 阿羅考上研究生．在哈羅德·霍特林（Harold Hotelling)的指導下攻讀數理經濟學 他發現，邏輯學在經濟學中大有用武之地 就拿消費者的最優決策來說吧， 消費者從許多商品組合中選出其最偏好的組合、這正好與邏輯學上的排序概念吻合。又如廠商理論總是假設廠商追求利潤最大化， 當考慮時間因素時， 因為將來的價格是未知的 廠商只能力圖使基於期望價格的期望利潤最大化。我們知道、現代經濟中的企業一般是由許多股東所共同擁有100個股東對將來的價格可能有100種不同的期望，相應地根據期望利潤進行諸如投資之類的決策時便有100種方案。那麼， 問題如何解決呢?一個自然的辦法是由股東(按其占有股份多少)進行投票表決， 得票最多的方案獲勝 這又是一個排序問題阿羅所受的邏輯訓練使他自然而然地對這種關係的傳遞性進行考察 結果輕而易舉地舉出了一個反例。

　　阿羅第一次對社會選擇問題的嚴肅思考就這樣成為他學習標準廠商理論的一個副產品不滿足傳遞性的反例激起了阿羅的極大興趣，但同時也成為他進一步研究的障礙 因為他覺得這個悖論素未謀面但又似曾相識。事實上這的確是一個十分古老的悖論， 是由法國政治哲學家、概率理論家貢多賽在1785年提出的 但是阿羅那時對貢多賽和其他原始材料一無所知， 於是暫時放棄了進一步的研究。這是1947年。

　　次年， 在芝加哥考爾斯(Cowles)經濟研究委員會， 阿羅出於某種原因對選擇政治學發生了濃厚的興趣： 他發現在某些條件下，“少數服從多數”的確可以成為一個合理的投票規則。但是一個月後， 他在《政治經濟學雜誌》里發現布萊克(Black)的一篇文章已捷足先登， 這篇文章表達了同樣的思想看來只好再一次半途而廢了。阿羅沒有繼續研究下去其實還有另一層的原因，就是他一直以 嚴肅的 經濟學研究為己任， 特別是致力於運用一般均衡理論來建立一個切實可行的模型作為經濟計量分析的基礎 他認為在除此以外的“旁門左道’中深究下去會分散他的精力。

　　1949年夏天， 阿羅擔任蘭德公司(Rand)的顧問。這個為給美國空軍提供咨詢而建立起來的公司那時的研究範圍十分廣泛，包括當時尚屬鮮為人知的對策論。職員中有個名叫赫爾墨(Helmer) 的哲學家試圖將對策論應用於國家關係的研究， 但是有個問題令他感到十分棘手： 當將局中人詮釋為國家時，儘管個人的偏好是足夠清楚的， 但是由個人組成的集體的偏好是如何定義的呢?阿羅告訴他， 經濟學家已經考慮過這個問題， 並且一個恰當的形式化描述已經由伯格森(Bergson)在1938年給出。伯格森用一個叫做社會福利函數的映射來描述將個人偏好彙集成為社會偏好的問題， 它將諸個人的效用組成的向量轉化為一個社會效用 雖然伯格森的敘述是基於基數效用概念的， 但是阿羅告訴赫爾墨， 不難用序數效用概念加以重新表述。於是赫爾墨順水推舟， 請阿羅為他寫一個詳細的說明，當阿羅依囑著手去做時， 他立即意識到這個問題跟兩年來一直困擾著他的問題實際上是一樣的。既然已經知道“少數服從多數“一般來說不能將個人的偏好彙集成社會的偏好， 阿羅猜測也許會有其他方法。幾天的試探碰壁之後， 阿羅懷疑這個問題會有一個不可能性的結果。果然， 他很快就發現了這樣一個結果； 幾個星期以後， 他又對這個結果作進一步加強。

　　阿羅不可能定理就這樣呱呱墜地了。

　　從1947年萌發胚芽到1950年開花結果，阿羅不可能定理的問世可謂一波三折， 千呼萬喚始出來， 而且頗有點 無心插柳的意味。但是，正是在這無心背後的對科學鍥而不捨的追求，才使邏輯學在社會科學這塊他鄉異壤開出一朵千古留芳的奇葩， 這不能不說是耐人尋味的。

　　阿羅不可能定理(Arrow's impossibility theorem)的主要內容是：在非獨裁的情況下，不可能存在適用於所有個人偏好類型的社會福利函數。更具體地說，阿羅認為，任何一個合理的社會福利函數起碼應該滿足如下要求：

　　①其定義域不受限制，即它適用於所有可能的個人偏好類型。

　　②非獨裁，即社會偏好不以一個人或者少數人的偏好所決定。

　　③帕累托原則，即如果所有人都偏好A勝於B，則社會也偏好A勝於B。

　　④無關變化的獨立性，這一要求可以簡單理解為：只要所有人對A和B的偏好不變(不管對例如A和C的偏好如何變化)，則社會對A和B的偏好不變。阿羅證明：滿足上述四個條件且具有傳遞性偏好次序的社會福利函數不存在。他指出，多數規則(majorityrule)的一個根本缺陷就是在實際決策中往往導致迴圈投票。^[3]

　　阿羅的不可能定理源自孔多塞的“投票悖論”，早在十八世紀法國思想家孔多塞就提出了著名的“投票悖論”：假設甲乙丙三人，面對ABC三個備選方案，有如圖的偏好排序。

　　甲（a ＞ b ＞ c）

　　乙（b ＞ c ＞ a）

　　丙（c ＞ a ＞ b）

　　註：甲（a ＞ b ＞ c）代表——甲偏好a勝於b，又偏好b勝於c。

　　1.若取“a”、“b”對決，那麼按照偏好次序排列如下：

　　甲（a ＞ b ）

　　乙（b ＞ a ）

　　丙（a ＞ b ）

　　社會次序偏好為（a ＞ b ）

　　2.若取“b”、“c”對決，那麼按照偏好次序排列如下：

　　甲（b ＞ c ）

　　乙（b ＞ c ）

　　丙（c ＞ b ）

　　社會次序偏好為（b ＞ c ）

　　3.若取“a”、“c”對決，那麼按照偏好次序排列如下：

　　甲（a ＞ c ）

　　乙（c ＞ a ）

　　丙（c ＞ a ）

　　社會次序偏好為（c ＞ a ）

　　於是我們得到三個社會偏好次序——（a ＞ b ）、（b ＞ c ）、（c ＞ a ），其投票結果顯示“社會偏好”有如下事實：社會偏好a勝於b、偏好b勝於c、偏好c勝於a。顯而易見，這種所謂的“社會偏好次序”包含有內在的矛盾，即社會偏好a勝於c,而又認為a不如c！所以按照投票的大多數規則，不能得出合理的社會偏好次序。

　　阿羅不可能定理說明，依靠簡單多數的投票原則，要在各種個人偏好中選擇出一個共同一致的順序，是不可能的。這樣，一個合理的公共產品決定只能來自於一個可以勝任的公共權利機關，要想藉助於投票過程來達到協調一致的集體選擇結果，一般是不可能的。

　　為了簡單起見，假定，每個個體至少有3個供排列的選項，可以用各種味道的餅干為選項的例子，如，香草餅干(V)、巧克力餅干(C)和草莓餅干(S)，每一個人要形成一個序列，表示出他對3種味道的喜愛程度，如V>S>C，表示這個人最喜歡香草餅干，其次是草莓餅干，最後是巧克力餅干。設有甲乙丙三人作選擇，他們的個人偏好為：

　　甲： V>C>S

　　乙： C>S>V

　　丙： S>V>C

　　表1 投票悖論^[4]

投票者	對不同選擇方案的偏好次序
甲	V	C	S
乙	C	S	V
丙	S	V	C

　　用民主的多數表決方式，如果三個人都能充分表達自己的意見，則結果必然如下所示：

　　首先，在V和C中選擇，甲、丙喜歡V，乙喜歡C；

　　然後，在C和S中選擇，甲、乙喜歡C，丙喜歡S；

　　最後，在V和S中選擇，乙、丙喜歡S，甲喜歡V。

　　這樣三個人的最終表決結果如下：

　　V>C，C>S，S>V可見，利用少數服從多數的投票機制，將產生不出一個令所有人滿意的結論，這就是著名的“投票悖論”(paradox of voting)。這個投票悖論最早是由康德爾賽(Coudorcet，Marquis de)在l8世紀提出的，因而該悖論又稱為“康德爾賽效應”，而利用數學對其進行論證的則是阿羅。

　　用數學語言來說，即：假設群體S上有m個個體成員，群體中出現的各種事件構成一個集合X，每個個體對每一事件都有自己的態度，即每個人都對集合X有一個偏好關係 > _i=1，2，…，m。即可以按自己的偏好為事件排序。定義群體的偏好為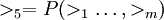：　其中P是一種由每個個體偏好得出群體偏好的規則。按這個規則從個體排序(偏好)得到群體排序(偏好)，而且這個排序符合民主社會的民主決策的各種要求。註意這個排序是自反的，即如果A>B，那麼，B<A；是可傳遞的，即如果A>B，B>C，則有A>C；並且還是完全的，即要麼A>B，要麼B>A，二者只有其一而且必有其一。這首先要考察一下民主社會的民主決策的各種要求是什麼，阿羅用4個公理(有時表述為5條，把公理1分為兩條)表述出這些要求。他用的是數學方法，符號化的公理和數理邏輯的證明方法，為了簡單地說明問題，我們採用了自然語言解釋。

　　公理1 個體可以有任何偏好；而且是民主選擇——每個社會成員都可以自由地按自己的偏好進行選擇(數學上稱為原則U—無限制原則： > _i，u=1，2，… ，　m在x上的定義方式無任何限制)。

　　公理2 不相干的選擇是互相獨立的；(數學上稱為原則I— —獨立性原則：對於X中的兩個事件X和Y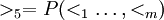，對它們做出的偏好判斷與X中的任何其他事件無關)。

　　公理3 社會價值與個體價值之間有正向關聯；(數學上稱為原則P—一致性原則：如果對X中的兩個事件X和Y，對於所有的i都有x < _iY，那麼X < _sY。這裡x < _iY表示X > _iY不成立。就是說，每人都有同樣明確態度的兩件事，社會也應該有同樣的態度。)

　　公理4 沒有獨裁者——不存在能把個體偏好強加給社會的可能。(數學上稱為原則D—— 非獨裁原則：不存在某個i，使得阿羅證明，滿足這4條公理表述的要求的民主決策的規則是不存在的，就是著名的“阿羅不可能性定理”：如果X中的事件個數不小於3，那麼就不存在任何遵循原則U，P，I，D的規則(稱為“社會福利函數”)。這表明滿足所有一般條件的民主選擇要麼是強加的，要麼就是獨裁的結果。

　　換句話說，阿羅不可能性定理指出，多數規則(majorily rule)的一個根本缺陷就是在實際決策中往往導致迴圈投票。

　　在得多數票獲勝的規則下，每個人均按照他的偏好來投票。不難看出，大多數人是偏好X勝於Y，同樣大多數人也是偏好Y勝於Z。按照邏輯上的一致性，這種偏好應當是可以傳遞的(transitivity)，即大多數人偏好X勝於Z。但實際上，大多數人偏好Z勝於X。因此，以投票的多數規則來確定社會或集體的選擇會產生迴圈的結果。結果，在這些選擇方案中，沒有一個能夠獲得多數票而通過，這就是“投票悖論”，它對所有的公共選擇問題都是一種固有的難題，所有的公共選擇規則都難以避開這兩難境地。

　　那麼，能不能設計出一個消除迴圈投票，做出合理決策的投票方案呢?阿羅的結論是：根本不存在一種能保證效率、尊重個人偏好、並且不依賴程式(agenda)的多數規則的投票方案。簡單地說，阿羅的不可能定理意味著，在通常情況下，當社會所有成員的偏好為已知時，不可能通過一定的方法從個人偏好次序得出社會偏好次序，不可能通過一定的程式準確地表達社會全體成員的個人偏好或者達到合意的公共決策。

　　這個結果是令人震動的：一個社會不可能有完全的每個個人的自由—— 否則將導致獨裁；一個社會也不可能實現完全的自由經濟—— 否則將導致壟斷。人們對社會的認識達到一個新的高度。因此阿羅的不可能定理一經問世便對當時的政治哲學和福利經濟學產生了巨大的衝擊，甚至招來了上百篇文章對他的定理的駁斥。李特爾、薩繆爾森試圖以與福利經濟學不相干的論點來駁倒阿羅的不可能定理，但又遭到肯普、黃有光和帕克斯的反駁，他們甚至建立了在給定個人次序情況下的不可能性結果。

　　事實上，阿羅的不可能性定理經受住了所有技術上的批評，其基本理論從來沒有受到重大挑戰，可以說是無懈可擊的，於是阿羅不可能定理似乎成為規範經濟學發展的一個不可逾越的障礙。怎樣綜合社會個體的偏好，怎樣在理論上找到一個令人滿意的評價不同社會形態的方法，成為一個世界性難題。這時候出現了阿馬弟亞·森(Amartya Kumar Sen，1933一)從20世紀60年代中期起，森在工具性建設方面的貢獻減少了這種悲觀主義色彩。森在這方面的研究推動了規範經濟學跨越這個障礙向前發展。他的研究工作不僅豐富了社會選擇理論的原則，而且開闢了一個新的、重要的研究天地。森1970年的著作《集體選擇和社會福利》是其最重要的一部著作，它使許多研究者恢復了對基本福利的興趣。另外這本書還具有哲學的風格，為規範問題的經濟分析提供了一個新的視角，剋服了阿羅不可能定理衍生出的難題，從而對福利經濟學的基礎理論作出了巨大的貢獻。

　　森所建議的解決方法其實非常簡單。森發現，當所有人都同意其中一項選擇方案並非最佳的情況下，阿羅的“投票悖論”就可以迎刃而解。比如，假定所有人均同意V項選擇方案並非最佳，這樣上面的表1就變為表2，僅僅甲的偏好由於同意“V並非最佳”而V和C的順序互換了一下，別的都不變。

　　表2 投票悖論的解決

投票者	對不同選擇方案的偏好次序
甲	C	V	S
乙	C	S	V
丙	S	V	C

　　在對V和C兩種方案投票時，C以兩票(甲乙)對一票(丙)而勝出於V(C>V)；同理，在對V和S以及C和S分別進行投票時，可以得到S以兩票(乙丙)對一票(甲)而勝出於V(S>V)；C以兩票(甲乙)對一票(丙)而勝出於S(C>S)。這樣，C>S—S>V—C>V，投票悖論就此宣告消失，唯有C項選擇方案得到大多數票而獲勝。

　　森把這個發現加以延伸和拓展，得出瞭解決投票悖論的三種選擇模式：

　　(1)所有人都同意其中一項選擇方案並非最佳；

　　(2)所有人都同意其中一項選擇方案並非次佳；

　　(3)所有人都同意其中一項選擇方案並非最差。

　　森認為，在上述三種選擇模式下，投票悖論不會再出現，取而代之的結果是得大多數票者獲勝的規則總是能達到唯一的決定。

　　一個更完整、更簡單也更具一般意義的不可能性定理，是艾利亞斯在2004年發表的。這一定理聲稱：如果有多於兩個可供選擇的社會狀態，那麼，任何社會集結運算元，只要滿足“偏好逆轉”假設和“弱帕累托”假設，就必定是獨裁的。特別地，阿羅的社會福利函數和森的社會選擇函數，都是社會集結運算元的特例，並且偏好逆轉假設在阿羅和繆勒各自定義的社會選擇框架內分別等價於阿羅的“獨立性假設”和繆勒的“單調性假設”，從而阿羅的不可能性定理、森的最小自由與帕累托效率兼容的不可能性定理、繆勒和塞特斯維特的一般不可能性定理，均可視為艾利亞斯一般不可能性定理的特例。艾利亞斯的不可能性定理有怎樣的經濟學和社會學結論是人們正在研究的問題。

　　阿羅不可能定理指出，通過反映社會中所有個體的偏好而進行的民主投票是不能產生社會福利函數的。阿羅認為，任何建立在個人偏好基礎上的公眾決策機制必須滿足一些基本要求：

　　一是集體理性。即如果所有個人的偏好具備完備性、傳遞性和自反性，則任何決策機制所導出的集體偏好也必須具備這些特性。

　　二是無限制性。公眾決策機制不得排斥任何形式的個人偏好，只要該偏好具備完備性、傳遞性和自反性。

　　三是帕累托較優性。如果每個人都認為方案A比方案B優越，那麼集體偏好也必須認為方案A比方案B優越。

　　四是偏好獨立性。集體偏好對方案A和方案B之問的排名只取決於人們對這兩種選擇之間的排名，而跟人們對其他選擇的排名無關。

　　阿羅不可能定理指出，完全滿足上述條件的公眾決策必然是一個獨裁決策，即以一個人的偏好順序代替所有的社會偏好順序，而這與建立在個人偏好基礎上的公眾決策機制是相違背的。因此說，滿足上述4項條件的公眾決策機制是不存在的。

　　現在，西方經濟學家們已經認識到，雖然阿羅不可能定理使福利經濟學籠罩在一片悲觀的氣氛之中，但是它對福利經濟學發展所起的作用卻是很重要的。因為18和19世紀就已經有人註意到集體決策可能導致矛盾的結果，但直到阿羅才對這一問題給出了一個一般性的結論，免去了人們許多無謂的研究。更為重要的是，阿羅不可能性定理使西方經濟學家們重新對社會選擇問題進行了深入的研究，並試圖尋找避免不可能性這一悲觀結論的方法。經濟學家的研究表明，阿羅不可能定理只適用於投票式的集體選擇規則，並不具備普遍意義。

　　案例適用：帕累托最優狀態

　　案例內容：

　　在我們的心目中，選舉的意義恐怕就在於大家根據多數票原則，通過投票推舉出最受我們愛戴或信賴的人。然而，通過選舉能否達到這個目的呢?1972年諾貝爾經濟學獎獲得者、美國經濟學家阿羅採用數學中的公理化方法，於1951年深入研究了這個問題，並得出在大多數情況下是否定的結論，那就是鼎鼎大名的“阿羅不可能定理”。阿羅不可能定理是指在一般情況下，要從已知的各種個人偏好順序中推導出統一的社會偏好順序是不可能的。我們對此加以證明。

　　假定有張三、李四、王五三個人，他們為自己最喜歡的明星發生了爭執，他們在劉德華、張學友、郭富城三人誰更受觀眾歡迎的問題上爭執不下。張三排的順序是劉德華、張學友、郭富城。李四排的順序是張學友、郭富城、劉德華。王五排的順序是郭富城、劉德華、張學友。到底誰更受歡迎呢?沒有一個大家都認可的結果。如果規定每人只投一票，三個明星將各得一票，無法分出勝負，如果將改為對每兩個明星都採取三人投票然後依少數服從多數的原則決定次序，結果又會怎樣呢?

　　首先看對劉德華和張學友的評價，由於張三和王五都把劉德華放在張學友的前邊，二人都會選擇劉德華而放棄張學友，只有李四認為張學友的魅力大於劉德華，依少數服從多數的原則，第一輪劉德華以二比一勝出；再看對張學友和郭富城的評價，張三和李四都認為應把張學友放在郭富城的前邊，只有王五一人投郭富城的票。在第二輪角逐中，自然是張學友勝出；接著再來看對劉德華和郭富城的評價，李四和王五都認為還是郭富城更棒，只有張三認為應該把劉德華放在前邊，第三輪當然是郭富城獲勝。

　　通過這三輪投票，我們發現對劉德華的評價大於張學友，對張學友的評價大於郭富城，而對郭富城的評價又大於劉德華，很明顯我們陷入了一個迴圈的境地。這就是“投票悖論”，也就是說不管採用何種游戲規則，都無法通過投票得出符合游戲規則的結果。如果世界上僅限於選明星的事情就好辦多了，問題在於一些關係到國家命運的事情的決定上，也往往會出現上述的“投票悖論”問題。對此很多人進行了探討，但都沒有拿出更有說服力的辦法。

　　在所有人為尋找“最優公共選擇原則”奔忙而無獲的時候，美國經濟學家阿羅經過苦心研究，在1951年出版的《社會選擇與個人價值》提出他的不可能定理。併為此獲得了1972年諾貝爾經濟學獎。阿羅不可能定理的意思是，“只要給出幾個選擇者都必然會接受的前提條件，在這些前提條件的規定下，人們在一般或普遍意義上不可能找到一套規則(或程式)在個人選擇順序基礎上推導出來”。由此進一步推出，在一般或普遍意義上，無法找到能保證所有選擇者福利只會增加不會受損的社會狀態。

　　阿羅所說的幾個選擇者必然接受的條件是：廣泛性。至少有三個或三個以上的被選方案，以供選擇者選擇；一致性。既一定的社會選擇順序以一定的個人選擇為基礎，但必須符合公眾的一致偏好；獨立性。不相關的方案具有獨立性；獨立主權原則。對備選方案的選擇和確定，應由公民完全依據個人的喜好而定，不能由社會強加；非獨裁性。不能讓每一個人的喜好決定整個社會對備選方案的排序順序，應堅持自由和民主的原則。

　　阿羅認為上述五個相互獨立的條件每一個都是必要的，但是要構造能同時滿足這些條件的社會福利函數是不可能的。導致不可能的原因在於1—5個條件之間存在相互矛盾，因此不可能達到完全一致。他從中得出了一個似乎不可思議的結論：沒有任何解決辦法能夠擺脫“投票悖論”的陰影，在從個人偏好過渡到社會偏好時，能使社會偏好得到滿足，又能代表廣泛的個人偏好這樣一種排序方法，只有強制與獨裁。這樣尋找合理的社會選擇機制的努力就幾乎陷入了困境。

　　阿羅不可能定理，打破了一些被人們認為是真理的觀點，也讓我們對公共選擇和民主制度有了新的認識。因為我們所推崇的“少數服從多數”的社會選擇方式不能滿足“阿羅五個條件”如市場存在著失靈一樣，對公共選擇原則也會導致民主的失效。因此多數票原則的合理性是有限度的。

　　　6.肯尼斯·阿羅．社會選擇和個人價值[M]．陳志武，等譯．成都：四川人民出版社，1987：174-179．

　　　7.史樹中．諾貝爾經濟學獎與數學[M]．北京：清華大學出版社，2002．33-34．

　　　8.汪丁丁．創造財富與毀滅財富的公共選擇機制[J／OL]．2005-7-15．