經濟計量分析
出自 MBA智库百科(https://wiki.mbalib.com/)
經濟計量分析（econometric analysis）
目錄 |
經濟計量分析是用統計推論方法對經濟變數之間的關係作出數值估計的一種數量分析方法。它首先把經濟理論表示為可計量的數學模型即經濟計量模型，然後用統計推論方法加工實際資料，使這種數學模型數值化。這種分析方法有兩個特點：①理論與觀察資料相結合，賦予理論以經驗的內容；②將隨機因素對經濟關係的影響納入分析之中，得出的結論具有概率性。
經濟計量分析產生於20世紀初，20年代以後就迅速發展起來。1926年挪威經濟學家R.弗里希（1895～1973）把它作為一門學科命名為經濟計量學（econometrics）。1930年一個國際性的“經濟計量學會”在美國成立，並從1933年起出版專門刊物《經濟計量學》。50年代特別是60年代以後，經濟計量分析的方法又有長足的發展，應用日益廣泛。對經濟計量分析方法作出重要貢獻的學者有挪威的弗里希、荷蘭的J.丁伯根（1903～ ）、美國的L.R.克萊因（1920～ ）等。
經濟計量分析的主要內容是建立模型、估計參數和運用模型。
建立模型
根據經濟理論、可利用的資料和現有的經濟計量技術，確定經濟變數之間關係的數學形式，這是經濟計量分析的第一步。它包括以下三方面的決定：①模型包括哪些經濟變數、哪些經濟關係式。②每個經濟關係式的函數形式。③參數的符號和取值範圍。根據所研究問題的複雜程度，模型可以是單一方程，也可以是聯立方程組。模型中的變數必須區分內生變數和外生變數。內生變數是由模型的求解來決定其數值的變數，外生變數是在模型以外決定其數值的變數。外生變數給模型所反映的經濟系統以影響，而不受這個系統的影響。一個變數在模型中為內生變數或外生變數，決定於問題的性質與研究的目的，例如積累率在社會主義巨集觀經濟預測模型中常常作為外生變數，而它在經濟系統的優化模型中又常常作為內生變數。
在建立模型階段，各方程通常採取結構方程形式。結構方程式是指其變數間的關係比較直接、其經濟意義明顯的方程式。例如說明消費c與國民收入y之間關係的消費方程:c=α+β y，式中α、β為結構參數。結構方程按其所反映的經濟關係的性質分為四類：第一類叫行為方程。說明經濟主體（居民、企業、政府等）的經濟行為。例如表明消費者行為的需求函數。第二類叫工藝方程。說明生產中的工藝技術關係。例如反映生產中的人力、物力投入量與產出量之間關係的生產函數。第三類叫法規方程。說明法令、制度所規定的經濟關係，例如稅收方程。第四類是恆等式。說明均衡條件或部分與全體的關係。例如總供給等於總需求，消費加積累等於國民收入。
估計參數
經濟計量模型中的參數是指模型的各個方程中的常數。估計參數就是根據歷史資料，用數理統計方法推定這些常數的值。經濟計量分析中最常用的參數估計方法是最小平方法。其特點是：對於因變數與自變數的若幹組觀測值，按給定的函數形式確定因變數對自變數的回歸式，使得因變數的觀測值與其回歸值（以相對應的自變數代入回歸式而算出的值）之差的平方和為最小。設有因變數y與自變數x的n對觀測值（yi，xi），i=1，2，…，n。並設y與x有線性關係y=α+βx+u，其中u為零均值的隨機變數。最小平方法就是求一回歸直線：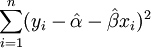
，使得為最小。數學上容易證明，滿足這一要求的
、
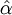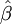值如下：
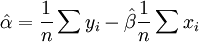
這就是α和β的最小平方估計量。
如果回歸方程中的隨機變數u的均值為0，具有常數方差。與自變數不相關，在各次觀測中彼此不相關，則用最小平方法得出的回歸繫數估計量是無偏的，且在所有線性無偏估計量中，它的方差是最小的。最小平方法因具有這樣的優良性質且計算簡單而被廣泛應用。
估算出來的參數需經過檢驗才能應用。檢驗的準則有兩類：一類是理論準則，它能指明參數的符號和取值範圍；另一類是統計準則，用以判斷參數估計值的統計可靠性。
運用模型
將已經估算好了參數的模型用之於結構分析、經濟預測和政策評價。結構分析的內容主要是測定模型內其他外生變數不變時某一外生變數變動一個單位或百分之一所引起的內生變數的絕對量變動或百分比變動。前一種場合，在絕對量上分析外生變數對內生變數的影響程度，稱為乘數分析。後一種場合，在相對量（即百分比）上分析外生變數對內生變數的影響程度，稱為彈性分析。經濟預測是將預計的未來時期的外生變數值代入模型之中，求解模型，得出未來時期內生變數的預測值。政策評價是根據模型計算和比較不同政策的不同後果，以便選取較好的政策。
