需求函數

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

需求函數(Demand function)

需求函數概述

　　需求函數(Demand function)：是用來表示一種商品的需求數量和影響該需求數量的各種因素之間的相互關係的。也就是說，影響需求數量的各種因素是自變數，需求數量是因變數。

　　需求函數是描述商品的需求量與影響因素，例如收入、價格、其它商品的價格等之間關係的數學表達式。

　　需求函數是單調減少函數。

[編輯]

需求函數模型

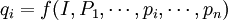
　　 $q_i=f(I,P_1,\cdots,p_i,\cdots,p_n)$

　　特定情況下可以引入其它因素。

[編輯]

從效用函數到需求函數

　　⑴ 從直接效用函數到需求函數

　　直接效用函數為：

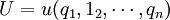
　　 $U=u(q_1,1_2,\cdots,q_n)$

　　預算約束為：

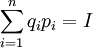
　　 $\sum^{n}_{i=1}q_ip_i=I$

　　在預算約束下使效用最大，即得到需求函數模型。

　　構造如下的拉格朗日函數：

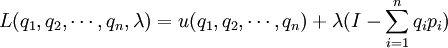
　　 $L(q_1,q_2,\cdots,q_n,\lambda)=u(q_1,q_2,\cdots,q_n)+\lambda(I-\sum^n_{i=1}q_ip_i)$

　　極值的一階條件：

　　 $\begin{cases}\frac{\partial L}{\partial q_i}=\frac{\partial u}{\partial q_i}-\lambda p_i=0\\\frac{\partial L}{\partial\lambda}=I-\sum^{n}_{i=1}q_ip_i=0\end{cases}$

　　求解即得到需求函數模型。

　　⑵ 從間接效用函數到需求函數

　　間接效用函數為：

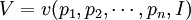
　　 $V=v(p_1,p_2,\cdots,p_n,I)$

　　利用公式

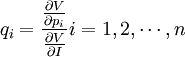
　　 $q_i=\frac{\frac{\partial V}{\partial p_i}}{\frac{\partial V}{\partial I}} i=1,2,\cdots,n$

　　可以得到所求的使效用達到最大的商品需求函數。

[編輯]

需求函數的0階齊次性

　　⑴ 需求的收入彈性

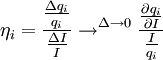
　　 $\eta_i=\frac{\frac{\Delta q_i}{q_i}}{\frac{\Delta I}{I}}\to^{\Delta\to 0}\frac{\frac{\partial q_i}{\partial I}}{\frac{I}{q_i}}$

　　⑵ 需求的自價格彈性

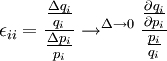
　　 $\epsilon_{ii}=\frac{\frac{\Delta q_i}{q_i}}{\frac{\Delta p_i}{p_i}}\to^{\Delta\to 0}\frac{\frac{\partial q_i}{\partial p_i}}{\frac{p_i}{q_i}}$

　　⑶ 需求的互價格彈性

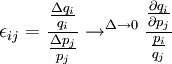
　　 $\epsilon_{ij}=\frac{\frac{\Delta q_i}{q_i}}{\frac{\Delta p_j}{p_j}}\to^{\Delta\to 0}\frac{\frac{\partial q_i}{\partial p_j}}{\frac{p_i}{q_j}}$

　　⑷ 需求函數的0階齊次性條件

　　當收入、價格、其它商品的價格等都增長倍時，對商品的需求量沒有影響。即

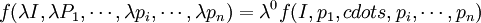
　　 $f(\lambda I,\lambda P_1,\cdots,\lambda p_i,\cdots,\lambda p_n)=\lambda^0f(I,p_1,cdots,p_i,\cdots,p_n)$

[編輯]

幾種重要的單方程需求函數模型及其參數估計

　　⒈ 線性需求函數模型

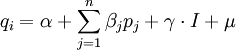
　　 $q_i=\alpha+\sum^{n}_{j=1}\beta_jp_j+\gamma\cdot I+\mu$

經驗中存在
缺少合理的經濟解釋
不滿足0階齊次性條件
OLS估計

　　⒉ 對數線性需求函數模型

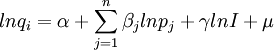
　　 $ln q_i=\alpha+\sum^{n}_{j=1}\beta_jln p_j+\gamma ln I+\mu$

經驗中比較普遍存在
參數有明確的經濟意義
每個參數的經濟意義和數值範圍？
可否用0階齊次性條件檢驗？
OLS估計

取自"https://wiki.mbalib.com/zh-tw/%E9%9C%80%E6%B1%82%E5%87%BD%E6%95%B0"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Angle Roh,Cabbage,Smileandblue,Dan,寒曦.

頁面分類: 經濟分析工具

評論(共3條)

提示:評論內容為網友針對條目"需求函數"展開的討論，與本站觀點立場無關。

115.188.14.* 在 2014年3月30日 19:25 發表

feihua

回複評論

凯撒幽兰 (討論 | 貢獻) 在 2018年5月27日 17:38 發表

115.188.14.* 在 2014年3月30日 19:25 發表

feihua

out there；#

回複評論

111.47.188.* 在 2021年3月29日 15:26 發表

為什麼不能用簡體中文啊？

回複評論

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

需求函數

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

需求函數概述

需求函數模型

從效用函數到需求函數

需求函數的0階齊次性

幾種重要的單方程需求函數模型及其參數估計

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共3條)

導航

意见反馈

查看

工具▼

需求函數

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

需求函數概述

需求函數模型

從效用函數到需求函數

需求函數的0階齊次性

幾種重要的單方程需求函數模型及其參數估計

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共3條)

導航

意见反馈