效用函數
出自 MBA智库百科(https://wiki.mbalib.com/)
效用函數(Utility Function / Effectiveness Function / Utility Function Used)
目錄 |
"效用函數" 在工具書中的解釋
表示消費者在消費中所獲得的效用與所消費的商品組合之間數量關係的函數。它被用以衡量消費者從消費既定的商品組合中所獲得滿足的程度。運用無差異曲線只能分析兩種商品的組合,而運用效用函數則能分析更多種商品的組合。其表達式是:U=U(x, y, z, …)式中 x, y, z分別代表消費者所擁有或消費的各種商品的數量。
"效用函數" 在學術文獻中的解釋
1、效用函數的定義是:設f是定義在消費集合X上的偏好關係,如果對於X中任何的x,y,xfy當且僅當u(x)u(y),則稱函數u:XnR+R是表示偏好關係f的效用函數。[1]
2、F(X)稱為效用函數.加權P範數法的關鍵是權繫數的確定.有2種基本的方法,一是老學習法[1,2],該方法依據目標函數的相對重要性來選取權繫數。[2]
3、一個人的效用應是財富x的函數,這個函數稱為效用函數,從理論上來講,它可以通過一系列心理測試來逼近得到每個人的效用函數.不同的決策者應有不同的效用函數.首先我們尋求效用函數所滿足的性質或某些特殊類效用函數所滿足的性質。[3]
4、這是一種理論假設,他們運用的數學函數式所建立的模型稱為“效用函數”.按照這類模型,人都能被假設成為可以決定在每一種可能的時間分配中產生一定的利益水平,並且追求利益最大化的選擇。[4]
T——第i種運輸方式的出行時間;
C——第i種運輸方式的運輸費用。[5]
6、為了對控制做出評價,需要一套函數作為評價指標: 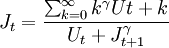 其中Ut = U[Rt,At,t]用以對每步控制進行評價,稱為效用函數.J(t)函數表示了從此刻開始的每步效用函數值的累積,稱為費用函數。[5]
其中Ut = U[Rt,At,t]用以對每步控制進行評價,稱為效用函數.J(t)函數表示了從此刻開始的每步效用函數值的累積,稱為費用函數。[5]
在現代消費者理論中,以商品價格向量P、消費束(商品數量向量)X、和消費者預算約束m三者為自變數的效用函數形式有兩類:一類是僅以消費束X為自變數的“直接效用函數”U(X);另一類是以商品價格向量P和消費者預算約束m兩者為自變數的“間接效用函數”v(P,m)。
直接效用函數U(X)的思想是:只要消費者購買(消費)各種商品的數量一定(而不管其他相關的經濟變數(如價格向量P)如何置定或變動),消費者的偏好或效用大小便唯一地確定。即,確定的消費束X對應確定的效用函數值U(X)。
間接效用函數v(P,m)是建立在僅以消費束X為自變數的直接效用函數U(X)的基礎之上的。其思路是:只要消費者面臨的商品價格向量P和消費者預算約束m兩者一定,消費者在PX=m約束下,最大化其直接效用函數U(X)的值,此時的最大U(X)值即是間接效用函數v(P,m)的函數值。需要特別指出的是,消費者面臨的商品價格向量P和消費者預算約束m兩者確定,消費者最大化其效用水平的購買消費束X並不要求唯一確定(雖然大多數時候是唯一確定的),但這些不同的向量X所對應的直接效用函數U(X)的值卻必須是唯一的“最大值”。
現代西方經濟學關於效用函數與商品價格向量P、消費束(商品數量向量)X、和消費者預算約束m等其他經濟變數的關係,被認定為:效用函數值的大小實際上被消費者本人的消費束X唯一地確定;除消費束X之外的其他變數(如P和m)對消費者效用水平的影響,只能通過影響X間接地決定或影響效用水平。即只要消費者購買(或消費)各種商品的數量一定(而不管其他相關的經濟變數如價格向量P如何置定或變動),其偏好或效用大小便唯一地確定。然而,實際情形並非如此。
效用函數的存在性,用數學式表示了效用函數的2個特征:效用是隨著單個商品數量遞增而增長的,且單個商品的邊際效用是遞減的同時,得出了對於效用函數,商品組合X和商品組合Y產生的效用之和大於商品組合X+Y產生的效用.
西方經濟學效用函數的存在性定理[6]:假定消費者偏好具有完備性、自返性、傳遞性、連續性和強單調性,那麼,存在著一個能代表該偏好的連續效用函數。
在上述假設下,西方經濟學首先構造一個由所有商品的1個單位所組成的單位消費束e(e是每個分量均為1的n維實數空間Rn中的向量),然後將所有的消費束與這個單位消費束進行比較,“證明”這些所有的消費束都分別與這個單位消費束的某一個倍數是無差異的,從而可以用這個倍數來表示效用,即效用函數是存在的。
但是,西方經濟學對效用函數的存在性的證明,是一種自我迴圈的論證。這是因為,效用函數存在性定理的那些假設條件,不是基於事實,而是基於數學證明的需要。而要滿足這些假設條件,就必須事先要求效用函數的存在。事實上,如果沒有效用函數的事先存在,消費者是不可能對數百萬種商品的各種數量的無窮組合進行滿足完備性、傳遞性和連續性的偏好判斷的。而這正是在心理實驗中發現那些事先沒有設定效用函數的人們的選擇缺乏傳遞性的根本原因。
從而西方經濟學所證明的是這樣一個定理:假定消費者偏好是用一個能夠被數學證明其存在性的連續效用函數來代表的,那麼就可以證明存在這樣一個能代表該偏好的連續效用函數。
進一步地,上述存在性定理所“證明”的效用函數是連續性的,從而是基數效用,而不是非連續的序數效用。也就是說,序數效用的存在性並沒有得到任何證明。而基數效用的最大問題是如何確定“效用單位”。對於一個“效用單位”到底是多少的問題,西方經濟學始終沒有回答。實際上,從西方經濟學關於效用函數存在性的“證明”過程來看,西方經濟學實際上隱含地將一個單位消費束即所有商品各消費一個單位所帶來的消費效用作為一個效用單位。但是,富人是不會去吃窮人的“珍珠翡翠白玉湯”的。這種湯帶給窮人的效用為正,而帶給富人的效用為負。從而,窮人和富人有不同的消費集,也就有了不同的單位消費束。那麼應當按哪一個消費束來算呢?尤其是對於那些財富的數量每天在變動的人,比如今天還是白領、明天就失業成為窮人的人。
還有一個問題就是一個商品的消費單位如何計算?比如,對於水和糧食,如果都用噸來計算,那麼我們可以設想這樣一個情形:假定對某個消費者來說,3噸水和0.1噸糧食是其在某個沙漠地區生存一段時間所必需的。用x=(3,0.1)來表示此消費束。也就是說,我們在這裡只考慮一個簡單的二維消費空間,其中的一維代表水,另一維代表糧食。於是,按照西方經濟學關於效用函數存在性的證明,存在某個0.1<t<3,使得t(1,1)即(t,t)與(3,0.1)是無差異的,也就是說消費t噸水和t噸糧食與消費3噸水和0.1噸糧食是無差異的。然而,在沙漠里,失去的(3-t)噸水是不可以用增加的(t-0.1)噸糧食來代替的[4]。當然,西方經濟學可以將3噸水和0.1噸糧食分別視為一個單位的水和一個單位的糧食,以便維持消費所需的正常比例。但是,這樣一來,各個商品的消費單位的認定就過於隨意了,而這種不同單位的轉換未必能保證存在性證明所需要的單調性,從而可能破壞效用的序數性質。
實際上,如果不能確定一個單位消費束中的所有商品的一個消費單位,那麼效用函數的存在性“證明”也就缺乏現實基礎。此外,我們註意到兩個單位消費束即2e的效用恰好是一個單位消費束e效用的兩倍,ne的效用恰好是e的效用的n倍。也就是說,如果將一單位消費束看作一個綜合商品,那麼該綜合商品的邊際效用是恆定的,與西方經濟學的邊際效用遞減相矛盾。
更進一步地,西方經濟學僅僅“證明”了效用函數的存在性,並沒有求出具體的效用函數。但西方經濟學卻因此獲得了可以任意設定效用函數的權力。例如,我們可以從西方經濟學教材中看到如下效用函數形式
u(x,y) = xayb
其中,x,y分別是兩個商品的消費量,U(x,y)是消費這樣一個消費束給消費者帶來的效用,a>0,b>0。
上述並未被數學證實的效用函數形式,存在這樣一個問題:考慮一個又飢又渴的人。設x,y分別代表水和麵包的消費量,則上述效用函數意味著,給這個消費者一粒麵包屑和無窮多的水,或者給這個消費者一滴水和無窮多的麵包,都可以讓該消費者得到無窮大的效用。但是,在現實生活中,上述兩個消費束帶給這個消費者的無窮大效用還不如兩杯水加兩個麵包帶給他的有限效用,後者更能適合他的需要。這個例子表明,西方經濟學不僅濫用了所謂效用函數的存在性,甚至無法給出一個不與人們的現實感受相衝突的具體的效用函數形式。
案例一:效用函數在金融學中的應用[7]
1952年,Markowitz發表《投資組合選擇》,揭開了金融數學的發展。半個世紀來,現代金融理論經歷了由簡單的定量分析到系統化,再到工程化的過程。這個過程中,效用函數成為研究金融理論的強有力工具。一些學者利用效用函數對Markowitz的均值一方差組合模型進行改進,形成了一些很實用的模型,比如金融學中常用的無差異曲線。有的學者考慮到投資者對收益與風險的偏好,建立了基於投資者的指數型效用函數和冪函數等,本文將討論效用函數的這兩種形式,並利用它們分析效用函數在保險業中的應用。
一、效用函數的冪函數形式
(1)對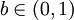 ,定義
,定義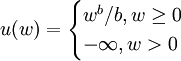
(2)對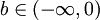 ,定義
,定義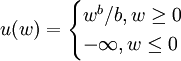
(3)對b=0,定義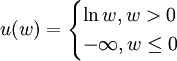
上述(3)中的形式實際上是因為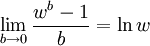
假定ζ > 0是一個有界的隨機變數,對上述3種形式,當w>0時,μ(w)都是嚴格凹函數,利用詹森不等式E(g(ζ)) < g(E(ζ))分別得到:
E(μ(ζ)) = E(ζb / b) < E(ζb) / b,
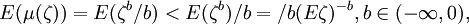 和E(μ(ζ)) = E(lnζ) < ln(Eζ),
和E(μ(ζ)) = E(lnζ) < ln(Eζ),
由此可見,此處預期效用最大化等同於 最大化,這就把問題轉化為數學問題。在投資分析中,利用效用函數的冪函數形式能夠很方便的解決一些問題。
二、效用函數的指數函數形式
(1)對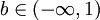 ,定義
,定義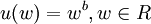 ;
;
(2)對b=0,定義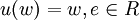
假定ζ > 0是一個有界的隨機變數,利用泰勒公式展開式,對(1)有:
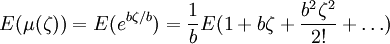
由上式可知,預期效用最大化等同於E(ζ)最大化且Varζ最小化及回報最大化兼顧風險最小化。因此風險與回報問題可以近似於效用函數的最優化問題。
如果 還服從正態分佈N(μ,σ2)即滿足E(ζ) = μ,Varζ = σ2。當貨幣收入效用函數具有形式(1)時,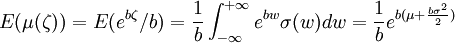 ,其中
,其中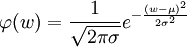 為正態分佈密度函數。註意到E(μ(ζ))是遞增的,因此如果是在某一單調變換下,預期效用函數E(μ(ζ))可變換為效用函數
為正態分佈密度函數。註意到E(μ(ζ))是遞增的,因此如果是在某一單調變換下,預期效用函數E(μ(ζ))可變換為效用函數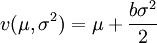 ,這兩個函數表示了同一偏好關係。因為v只和均值和方差有關,對風險行為作出回報與風險的評價要方便。
,這兩個函數表示了同一偏好關係。因為v只和均值和方差有關,對風險行為作出回報與風險的評價要方便。
三、購買保險與效用函數的形式
假定某人有初始財富收入為W(>0)元,且在一年後因意外原因會損失x(>0)元的概率為P,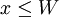 ;而保持初始財富W的概率為1-P,則他在一年後的預期收入為:
;而保持初始財富W的概率為1-P,則他在一年後的預期收入為:
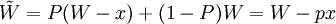 ,
,
此人面臨購買保險與不購買保險2種經驗選擇。
假定保險公司為人們提供保險並不想從個別人身上賺錢,也就是說,保險公司向個人銷售保險的預期收入為零(後面還討論保險公司的經營情況)。用π = RP(ζ)表示保險費,顯然0<π<x。如果意外事件發生,他將從保險公司得到x元的賠償。因此,保險公司銷售x元保險的預期收入為:p(π − x) + (1 − p)π = π − px。
在保險公司向個人銷售保險的預期收入為零的假設下,容易得到:π = px,即保險費就等於個人可能的損失與意外事件發生概率的乘積。
假設此人願意支付保險費,並仍假定為п,則當意外事件發生時,他會得到 元保險公司的賠償。因為他不購買保險的預期效用為: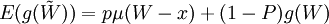 ,因此他購買保險的預期效用為μ(W − π),其中W − π就是他購買保險後的確定性收入。我們也可以計算得出,他的預期損失為utf − 8。如果保險費等於他的預期損失(這顯然具有合理性),則π = W − E(W − px) = px,則購買保險後的確定收人
,因此他購買保險的預期效用為μ(W − π),其中W − π就是他購買保險後的確定性收入。我們也可以計算得出,他的預期損失為utf − 8。如果保險費等於他的預期損失(這顯然具有合理性),則π = W − E(W − px) = px,則購買保險後的確定收人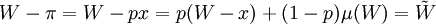 ,即保險所保證的穩定收入等於無保險情況下的財富收入的預期值。
,即保險所保證的穩定收入等於無保險情況下的財富收入的預期值。
由上面的分析得到,保險公司向個人銷售保險的預期收入為零所確定的保險費與購買保險者要求保險費要等於預期損失是一致的,因此也是科學的。
假定他是一個風險厭惡者,其效用函數是嚴格凹的,這時有,
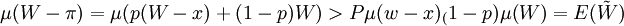
此式表明,購買保險的預期費用大於收入的預期效用,因此,購買保險對他來說是有利的,因此風險厭惡者願意購買各種各樣的保險。
下麵我們解方程:
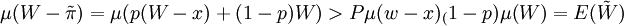
以此來求出他願意支付的最高保險成本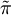 ,同時利用邊際效用μ(w) > 0,即μ(w)嚴格單調遞增,可知
,同時利用邊際效用μ(w) > 0,即μ(w)嚴格單調遞增,可知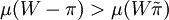 ,得出
,得出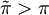 ,這說明最高保險費大於預期損失,此時作為理性人,他不會購買保險。同時,如果保險公司收取了較高的財產保險費,理性人會採取觀望態度,保險公司的經營會受到影響。
,這說明最高保險費大於預期損失,此時作為理性人,他不會購買保險。同時,如果保險公司收取了較高的財產保險費,理性人會採取觀望態度,保險公司的經營會受到影響。
下麵我們討論保險公司的經營狀況。
鑒於保險公司向個人銷售保險的預期收入為零,有人認為,這樣保險公司不但不會賺錢,還要在經營中花掉管理費用、員工薪水等,保險公司就會虧本。事實並非如此。
事實上,保險公司作為經濟人,也是以追求利潤最大化為唯一目的。保險公司是投機者,只要他們有數量可觀的保險單,他們就幾乎沒有什麼風險。這可以由概率的大數定律來解釋:雖然在一次實驗中某事件發生的概率是隨機的,但是在大量的重覆獨立實驗中,該事件發生的頻率卻收斂於確定的常數。這樣保險公司可以通過大面積操作來規避風險,達到盈利的目的。我們以人身保險為例說明。
某城鎮每人每年的意外死亡率為0.006,若某人意外死亡,保險公司將賠付被保險人100000元,保險費為600元。假設有10000人購買此保險。則公司利潤為:
10000×600-死亡人數×100000=(60-死亡人數)×100000.
每人每年死亡可看成是進行10000次重覆獨立的試驗,即貝努里試驗,設ζ表示10000人中意外死亡人數,則ζ~b(10000,0.006)即。
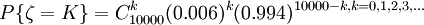
公司虧本的可能性,即為
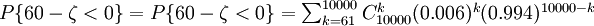 ,
,
利用De Moire-Laplace積分極限定理:
P{公司虧本}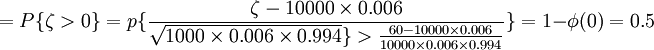
由於意外死亡發生的概率很小,每人對意外死亡規避度很高,保險公司並不用擔心虧本的可能性只有0.5。
一般來說,保險公司會收取較高意外死亡保險費,並不影響該公司的業務。例如,保險費定為800元, 這時,P{公司虧本}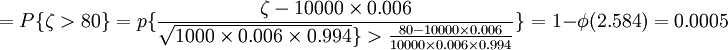
所以,保險公司幾乎不會虧本。
效用函數的具體形式很多,比如完全替代效用函數、線性效用函數等等,本文只介紹了效用函數的冪函數形式和指數函數形式,因為金融學中這2種形式比較常用。在日常生活中,消費者都在有意無意地利用著效用函數進行消費,無論他們是否知道效用函數的具體形式。效用函數已經成為用數學方法研究經濟問題的鋪路石,通過對效用函數的數理分析,使經濟學和金融學更有邏輯性。在解決實際問題中,我們可以根據一些具體條件和約束條件,建立最優化模型。根據對其效用函數性質的討論,我們可以得到該模型唯一的最優解,而不用效用函數形式的不唯一性。
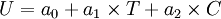 ;
;








該條目非常好,對於初學者而言,很有意義。