風險敞口
出自 MBA智库百科(https://wiki.mbalib.com/)
風險敞口(Risk Exposure),也叫風險暴露
目錄 |
風險敞口指未加保護的風險,是指對於風險未採取任何防範措施而可能導致出現損失的部分。
風險敞口又譯風險暴露,通常是指金融機構在各種、業務活動中容易受到風險因素影響的資產和負債的價值,或說暴露在風險中的頭寸狀況[1]。
- 已知風險的風險敞口是從零到該風險最大損失之間。未知風險的風險敞口是從零到無窮大。
- 某一特定資產的買賣可能增加你的風險暴露程度;而在另一種情況下,相同的交易又可能減少風險。
信貸風險敞口是指因債務人違約行為導致的可能承受風險的信貸餘額。
風險和風險暴露的關係[1]
風險與風險暴露根據對風險概念的分析,我們不難看出風險對於金融機構而言是客觀存在的,如利率、匯率等風險變數的波動性一般不會因為某個金融機構的行為或意願而發生改變。因此,嚴格地說,無論金融機構的風險管理水平如何,它們所面臨的風險是一樣的,並不能認為風險管理質量差的金融機構所面臨的風險比風險管理質量高的金融機構大。但在許多情況下,人們對風險一詞的使用比較含混,通常它不僅指這種客觀的風險因素的波動性,有時也包括投資者對風險的主觀暴露程度。
如對信用風險的暴露是指受到信用風險影響的貸款量,對利率或匯率風險的暴露則是受到利率或匯率變動影響的資產和負債的價值。因此,在一般的意義上,投資者所承擔的風險水平的高低不僅取決於風險因素波動性或不確定性的大小,更重要的是取決於其對特定風險因素的暴露程度。無論風險因素的波動性有多大,如果投資者能夠通過各種風險管理手段使得其對該風險因素的暴露程度為零,則他所面臨的風險實際上也為零。因此,金融機構風險管理的本質是對其風險暴露的管理,而巨集觀層次的風險管理則有可能是對風險因素自身的管理,如政府經濟管理部門為降低匯率、利率和股票總體價格水平的波動性而進行的努力。
風險敞口的度量[2]
使用回歸分析來評估風險敞口
回歸法是在分析風險和構築套期保值方案時最為流行的一種工具。它可以檢驗未經套期保值的企業現金流量歷史數據與風險要素之間的關係。具體來說,是根據企業的歷史收益或現金流量與風險要素之間的數量關係回歸來估計要素p繫數。在回歸模型中要素盧繫數就是曲線的斜率。
根據模擬法度量風險敞口
模擬法是一種具有前瞻性的風險評估方法。回歸法運用的是歷史數據,是一種事後檢驗的評估方法。對於當今變化發展相當迅速的產業來說,模擬法無疑勝於回歸法。
根據情景設想來實現模擬法。運用模擬法,管理者需要在不同要素實現的基礎上預測收益或現金流量。例如匯率風險,管理者需要明確說明在不同匯率下的各種情景。每一個情景設想下還要估計在不同假設條件下的利潤或現金流量的發生額,這些假設條件除了匯率變動情況以外,還包括該產業的產品需求情況、競爭對手情況和其他供應者對匯率變動的反應。
模擬法與回歸法。儘管模擬法要求分析者做出更多的主觀判斷,對於分析者來說可能有一定的難度,但是模擬法並不依賴公司過往的歷史業績來評估將來。事實上,這一點在一個持續變化的環境下是至關重要的。比如說,要估計通用公司的日元風險,一般都不可能僅僅通過對過去10年的數據進行回歸分析。在這10年間,通用公司的競爭對手——日本的汽車製造商,已經經歷了巨大的變化。而且,一個公司未來的日元風險敞口不可能與其。過轟的風險敞口是一樣的。
對根據回歸模型獲得的最初評估值進行調整。用模擬法分析匯率風險只需管理者估計在不同匯率情景假設下企業的未來成本和收益,並以此計算利潤(或現金流量)。回歸法可以為這些估計數據提供有用的信息,但同時管理者在分析時不應該局限於通過回歸法得出的結果.他(或她)還可以把產品的價格需求彈性、競爭對手的預期反應與回歸估計值結合起來分析。此外,回歸法認為利潤(或現金流量)與匯率變動之間存在著線性關係,然而這種關係在現實中存在的可能性很小。管理者要通過調整以回歸分析為基礎的評估值來解釋各因素數量關係中的非線性關係。
例如,通用公司假設日本的汽車製造商在日元小幅度升值時仍會保持其產品的美元價格不變,以此放棄部分利潤來確保市場份額。如果該假設成立的話,通用公司將不會從日元的小幅升值中獲利。然而,如果日元大幅升值,日本汽車製造商將發現放棄美國市場是明智之舉,這時通用公司就可以從中漁利了。
當日元貶值時,我們也可以利用類似的論證方法。日元貶值將利於日本汽車製造商,小幅貶值對於在美銷售的日本汽車的價格不會有什麼影響,這也許是因為日本的汽車製造商考慮到如果日元貶值後又大幅升值的話,他們還要被迫將價格再調升,這樣做不利於汽車市場價格的穩定。可是,如果日元大幅貶值的話,將會給日本的汽車製造商帶來巨大的成本優勢,他們無疑將充分利用這一機會來擴大市場份額,從而大幅削減通用公司的利潤。
根據基本原理預先確定要素β繫數
在某些情況下,要素β繫數可以通過基本原理預先確定。例如,德國金屬股份公司以預先決定的價格向客戶出售燃料油的這個承諾可以被視為一份遠期交易合約。如果風險要素是10年後的石油價格,那麼10年期的遠期合約的要素β繫數一定等於1。
波動率——風險敞口的度量指標
公司管理者總希望用一個數字來概括風險敞口。鑒於此,標準差常常被用來概括和分析多個要素β繫數組合的風險影響。計算一項投資的要素風險方差的公式為:
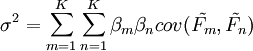
式中,βm為要素m的要素β繫數;βn為要素n的要素β繫數。
由要素風險而產生的現金流量或價值的波動率(即標準差)就是上述公式計算結果的平方根。
案例分析上式:
假設某公司一年後的現金流量(單位是百萬美元)根據以下要素模型計算:
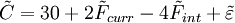
式中:貨幣要素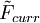 表示下一年美元匯率變化的百分比;利率要素
表示下一年美元匯率變化的百分比;利率要素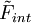 表示從3個月期(從現在開始)的LIBOR到1年期(從現在開始)的LIBOR的變動百分比,
表示從3個月期(從現在開始)的LIBOR到1年期(從現在開始)的LIBOR的變動百分比,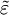 表示由以上兩種風險要素以外的其他因素引發的現金流量風險。假設貨幣要素方差的估值為0.011,利率要素方差約為0.022,兩者的協方差為0·004。求該現金流兩由要素風險引起的波動率。
表示由以上兩種風險要素以外的其他因素引發的現金流量風險。假設貨幣要素方差的估值為0.011,利率要素方差約為0.022,兩者的協方差為0·004。求該現金流兩由要素風險引起的波動率。
答案:根據上述方差公式,要素方差為:
σ2 = 4(0.011) − 8(0.004) − 8(0.004) + 16(0.022) = 0.332
波動性就是以上計算結果的平方根,即0.576(單位:百萬美元)。
顯然,風險要素的方差和協方差估計值是計算波動率並得到準確估值的關鍵。估計風險要素的協方差和方差的一種辦法就是計算以往的歷史方差及協方差。可是,金融機稗攣分析波動性時已經發現方差及協方差是隨時間不斷變動的,因此他們開發了更複雜的波動.
在險價值——風險敞口的度量指標
也許當今最為流行的風險敞口度量方式便是在險價值(value at risk,VAR)了,它是指正常市場條件和給定的置信水平下,金融參與者在給定的時間區間內可能發生的最大期望損失。例如,某項投資的頭寸在下一年中有不超過1%的時間,其最大投資損失將達到1億美元,因此一些管理者就會認為下一年的在險價值為1億美元。
在險價值的決定因素是時間區間以及投資者主觀認定的正常市場條件的標準。時間區間不同在險價值將不同。投資頭寸在下一年的在險價值是1億美元,如果把考慮的時間區間縮短,比如說一個月,那麼下一個月的在險價值將明顯小於下一年的在險價值。同理,如果預計市場非正常的不理想情況出現概率不超過5%,那麼分析者作出的在險價值評估將低於預計市場非正常情況出現概率不超過l%的分析者所作出的評估。
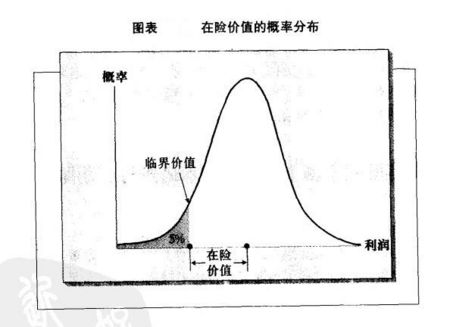
當使用描述利潤與損失的分佈圖來表示在險價值的時候,置信水平(5%或1%就是典型的決定非正常市場條件的特定極限)以及時問區間的重要性就會體現出來。圖表22.1表示了預計利潤為零的交易在置信水平為5%時的在險價值。時間區間影響分佈曲線的形狀。時間區間越長,利潤的不確定性就越大.正常的分佈曲線也越長。這將導致點A一一曲線左翼5%區域的邊界一一向左移動,從而增加了在險價值。左翼區域邊界極限的改變同樣也會改變在險價值,如果5%的邊界向左移動到1%的邊界,那麼在險價值也會因此而增加。
在險價值是評價衍生金融工具或者其他證券組合的價值時度量風險的一種標準分析方法。在這一標準化的過程中也有管理機構的推動作用。1996年底,國際結算銀行、美國證券交易委員會以及聯邦儲備委員會建議他們所監管的金融機構對某些金融活動的風險度量採用在險價值作為標準。另一種類似的方法被應用於分析現金流量風險,叫在險現金流(cash flow at risk,CAR)。這種方法也越來越受到各公司企業的重視。
根據標準差估計在險價值和在險現金流
如果價值或現金流是正態分佈的話,在險價值和在險現金流就是標準差的另一種表現形式。例如,
VAT(5%置信水平=1.65σ)
式中:σ是價值的標準差。除非是現金流的標準差,否則同樣地公式也適用於在險現金流(CAR)。
上述公式中的數據1.65來源於正態分佈表。特別要註意的是,在表中我們發現N(-1.65)大約是0.05。從更廣義的角度來分析,如果正態分佈的價值或現金流量的均值為0,標準差是σ,其概率小於P%,則可令x等於此價值或現金流,就有:N(x)=p%。因此,VAR或CAR就是 − xσ。
案例分析如何將σ轉換成CAR.
在正態分佈的假設下根據標準差計算CAR
在上個案例分鐘中,現金流量的標準差大概是576200美元。假設現金流量是正態分佈的,那麼在5%的置信水平下現金流量的在險價值是多少?
答案:1.65(576200美元)=950720美元
利用模擬法估計在險價值在險現金流。如果要估計在險現金流,模擬法比標準差公式有更好地適用性。一直確定的要素β繫數,我們就可以根據要素等式模擬現金流量,要素等式中的要素價值是通過觀察給定的歷史期限數據獲得的。在險現金流就是平均現金流量與歷史期限下的第五區間值之間的差額。
比如你的收入是日元,但你有一筆美元的借款要還,是沒有做任何對沖的交易(比如遠期外匯買賣或外匯調期什麼的),你因此就有了一個日元對美元的匯率風險敞口。
或者你買了一個公司的債券,由於公司債有信用風險,而且你沒有做任何對沖的交易(比如信用調期什麼的),你因此有一個信用風險敞口。
你如果買了一個固定利率的債券,而且沒有做對沖交易(比如利率調期),你要承擔利率風險,因此有一個利率風險敞口。








沒看懂哦