協方差
出自 MBA智库百科(https://wiki.mbalib.com/)
協方差(Covariance,COV)
目錄 |
在概率論和統計學中,協方差用於衡量兩個變數的總體誤差。而方差是協方差的一種特殊情況,即當兩個變數是相同的情況。
期望值分別為E(X) = μ 與 E(Y) = ν 的兩個實數隨機變數X與Y之間的協方差定義為:
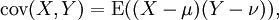
其中,E是期望值。它也可以表示為:
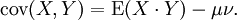
直觀上來看,協方差表示的是兩個變數總體的誤差,這與只表示一個變數誤差的方差不同。
如果兩個變數的變化趨勢一致,也就是說如果其中一個大於自身的期望值,另外一個也大於自身的期望值,那麼兩個變數之間的協方差就是正值。
如果兩個變數的變化趨勢相反,即其中一個大於自身的期望值,另外一個卻小於自身的期望值,那麼兩個變數之間的協方差就是負值。
如果X與Y是統計獨立的,那麼二者之間的協方差就是0。這是因為
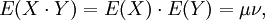
但是,反過來並不成立。即如果X與Y的協方差為0,二者並不一定是統計獨立的。
協方差cov(X,Y)的度量單位是X的協方差乘以Y的協方差。而取決於協方差的相關性,是一個衡量線性獨立的無量綱的數。
協方差為0的兩個隨機變數稱為是不相關的。
如果X與Y是實數隨機變數,a與b不是隨機變數,那麼根據協方差的定義可以得到:
對於隨機變數序列X1, ..., Xn 與 Y1, ..., Ym,有
對於隨機變數序列 X1, ..., Xn,有
分別為m與n個標量元素的列向量隨機變數X與Y,二者對應的期望值分別為μ與ν,這兩個變數之間的協方差定義為m×n矩陣。
兩個向量變數的協方差cov(X,Y)與cov(Y,X)互為轉置矩陣。
協方差有時也稱為是兩個隨機變數之間“線性獨立性”的度量,但是這個含義與線性代數中嚴格的線性獨立性線性獨立不同。
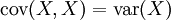
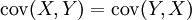
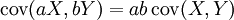
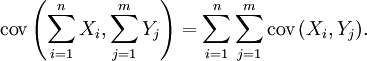
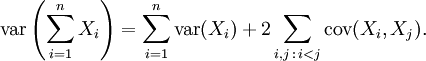
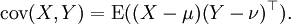








好久沒看數學。。。。。差點全忘光了。。。。。得註意了