社會福利函數

出自 MBA智库百科(https://wiki.mbalib.com/)

社會福利函數(social welfare function)

　　社會福利函數是福利經濟學研究的一個重要內容，它試圖指出社會所追求的目標應該是什麼，應該考慮哪些因素：是某些人的利益或效用，還是所有人的利益或效用？當人們之間的利益或效用相衝突時，應該如何處理這些不同的利益或效用？縱觀福利經濟學的發展歷史，社會福利函數的研究在經歷了古典效用主義時期、轉折時期之後，進入了困惑時期和古典效用主義復興時期。

　　需要知道在效用可能性曲線上每一點所代表的社會福利的相對大小，或者更一般地說，需要知道效用可能性區域或整個效用空間中每一點所代表的社會福利的相對大小。這就是所謂的社會福利函數。

　　社會福利函數把社會福利看作是個人福利的總和，所以社會福利是所有個人福利總和的函數。以效用水平表示個人的福利，則社會福利就是個人福利的函數。假設社會中共有n人，社會福利函數W可以記作：

　　W = f(U₁,U₂,...,U_n)

假定社會中共有A、B兩個人，這時的社會福利函數可以寫成：

　　W = f(U_A,U_B)

　　對於不同的社會福利水平W1、W2、…、Wn，可以得出一系列的等福利曲線，等福利曲線與效用可能性曲線的區別在於：效用可能性曲線是消費者在分配某一既定數量產品時可能得到的各種效用組合；而表示社會福利函數關係的等福利曲線則表示不同的效用組合可以達到的社會福利水平。

一、古典效用主義時期

　古典效用主義的社會福利函數把社會福利看作是所有社會成員的福利或效用的簡單加總，任何社會成員的福利都被平等對待，即w = u₁ + u₂ + ... + u_i，其中，代表社會成員福利水平的"u_i"是可以用具體數字1,2,3等等來度量的基數效用。我們看到，這種福利函數使用基數效用，只關心效用總量，因而忽視了收入分配問題。而更重要的是，對於基數效用本身，很多人有非議。

二、轉折時期

　　現代對社會福利函數的討論最初是由伯格森(A.Bergson)和薩繆爾森(Paul A.Samuelson)分別在1938年提出併在1947年加以進一步說明的。伯格森和薩繆爾森提出的社會福利函數被稱為伯格森—薩繆爾森的社會福利函數(bergson-samuel-son social welfare function)，它是一種實值的福利函數(real-valued welfare function)（因此簡稱為小寫字母的swf)。它認為，社會福利值w（用序數表示）取決於被認為影響福利的所有可能的實值變數z_i，即w = w(z₁,z₂,......)。這是一種一般化的函數，對於函數的具體形式沒有任何的規定，這是它的缺點，也是它的優點。因為沒有對函數的具體形式做出任何的規定，所以它只能是一種概念而已。事實上，薩繆爾森本人也曾說，如果不是許多人發現確定函數的形式變數的性質和約束條件的性質很有意義的話，這些無聊的話題也就到此為止了。但是，這種一般化的函數避開了價值判斷問題，它可以包括帕累托標準，也可以不包括，還可以包括其他的標準。不過，在許多問題的討論中，僅使用這種函數是不夠的，必須加入一定的價值判斷。

　　那麼，是否有一種系統化的方法可以獲得一種具體的伯格森—薩繆爾森社會福利函數呢？

　　肯尼斯·阿羅 (Kenneth J．Arrow)從1951年開始對這個問題進行研究，他提出了一種不同的社會福利函數，即阿羅社會福利函數(arrowian swf)。這一函數是指由定義在社會狀態集合x上的個人偏好排序r₁，確定社會排序r的某種社會決策規劃，即r=f｛(r_i)｝。這種函數不同於伯格森—薩繆爾森社會福利函數：它的函數值正好對應一種伯格森—薩繆爾森社會福利函數，因為伯格森—薩繆爾森社會福利函數是序數性質的。阿瑪蒂亞·森 (Amartya Sen)強調了這種區別。因此，阿羅社會福利函數被稱為大寫的swf，以區別於小寫的swf。

　　阿羅提出了著名的阿羅不可能性定理(arrow's impossibility theorem)，證明瞭在某些條件下阿羅社會福利函數是不存在的。實際上，阿羅證明的是阿羅一般性定理(general possibility theorem)，該定理證明阿羅社會福利函數必須至少滿足五個合理化的條件，即：符合邏輯的個人效用函數的任意性(free triple)；選擇的正或非負關聯性(positive or not negative association)；無關選擇的獨立性(independence of irrelevant alternatives)；非強迫性或公民的主權性(non-imposition or citizens' sovereignty)；非獨裁性(non-dictatorship)。（後來，證明過程有所修正，上述條件也略有變化。）但阿羅強調：遺憾的是，能夠同時滿足這五個條件的社會選擇機制是不存在的。阿羅不可能性定理使福利經濟學陷入了困惑之中。

三、困惑時期

　　困惑時期是指20世紀60年代。在這一時期，社會福利函數的研究處於停滯狀態，福利經濟學家們被不可能性的結論困惑著，他們在思考：究竟什麼樣的社會選擇機制才是可行的呢？到底阿羅式的社會福利函數存在什麼缺陷，從而使合理化的社會選擇機制不存在呢？對此，西方福利經濟學家們進行了種種努力。

　　現在，西方經濟學家們已經認識到：雖然阿羅不可能性定理使福利經濟學籠罩在一片悲觀的氣氛之中，但是它對福利經濟學發展所起的作用卻是很重要的。因為很早以前，例如18和19世紀就已經有人註意到集體決策可能導致矛盾的結果，但直到阿羅才對這一問題給出了一個一般性的結論，免去了人們許多無謂的研究。更為重要的是，阿羅不可能性定理使西方經濟學家們重新對社會選擇問題進行深入的研究（據森的研究，公元前4世紀的亞里士多德等人就有對此問題的討論），並試圖尋找避免不可能性這一悲觀結論的方法。阿馬蒂亞·森等人的研究表明，阿羅不可能性定理只適用於投票式的集體選擇規則，該規則無法揭示出有關人際間效用比較的信息，而阿羅式的社會福利函數實際上排除了其他類型的集體選擇規則，因而不可能性的結果是必然的。阿馬蒂亞·森於1998年度獲得諾貝爾經濟學獎，其重要貢獻之一即在於此。

四、古典效用主義復興時期

　　古典效用主義復興時期從20世紀70年代開始到現在。西方經濟學家們認識到，採用序數效用的新福利經濟學存在著不可剋服的缺陷，阿羅不可能性定理實際上就揭示了這種方法的局限性：在缺乏其他信息的情況下，只使用序數效用提供的信息進行社會排序是不可能的。森的進一步研究表明，使用基數效用可以獲得人際間效用比較方面的信息，從而可以得出一定的社會排序。同時，只要有人際間效用比較方面的信息，基數效用的使用並不是必需的，甚至序數式的人際間效用比較就足以逃出不可能性的結論了。這樣，在其他人研究的基礎上，黃有光於1975年提出了與古典效用主義相同的社會福利函數，並稱其為“完全的效用主義”的社會福利函數。他認為，由於經濟學家中普遍存在的“效用幻覺”，那種認為效用主義的社會福利函數忽視了收入分配問題的觀點是站不住腳的。這裡，我們看到，在越過了阿羅不可能性定理這一障礙之後，社會福利函數出現了向古典社會福利函數回歸的趨勢。

　　同一時期，採用基數效用的許多社會福利函數出現了，例如，新古典效用主義的社會福利函數(neo-utilitarianism swf):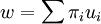其中，u_i表示如果作為社會中某個人i會具有的效用，π_i表示相應的概率。這一函數是維克裡(W.Vickery)和海薩尼(John C.Harsanyi)等人在古典效用主義的社會福利函數基礎上考慮了不確定性因素後所得到的結果。

　　又如，精英者的社會福利函數(elitist swf)，其函數形式是：w = max(u₁,u₂,...,u_i)，即社會福利水平取決於社會中效用最高或境況最好的那部分人的福利水平。該函數允許極度的兩級分化，因而受到廣泛的批評。與此相對的是羅爾斯主義的社會福利函數(rawlsian swf):w = min(u₁,u₂,...,u_i)，即社會福利水平取決於社會中效用最低的那部分人的福利水平。該函數假定每個社會成員都有最基本的自由，他們無法預知自己處於何種效用水平上，而且，每個人都是厭惡風險的，羅爾斯社會福利函數遵循的是最大最小標準，即社會福利最大化的標準應該是使境況最糟的社會成員的效用最大化，同時使所有人在機會平等的條件下都有事情可做。

　　再如，納什的社會福利函數(nash's swf):w = u₁u₂...u_i，即社會福利水平為所有社會成員效用水平的乘積。該函數形式有以下兩點不足：一是當某一效用水平為負其他效用水平為正時，社會福利水平也為負，而與其他社會福利水平為很小的正值的社會狀態相比，這實際上不一定是一種不可取的社會狀態；二是當某些效用水平為極小的純小數時，同樣會出現上述情況。

　　還有，阿特金森的社會福利函數(atkinson's swf): 該函數把社會成員分為窮人(p)和富人(r)兩部分，他們的間接效用函數分別為V^p和V^r，a為表示厭惡不平等的參數，a越大，表示社會越厭惡不平等，越重視窮人的效用，加在窮人效用水平上的權數越大。

　　目前，對社會福利函數的研究仍在繼續，但是，我們應看到，現代西方社會福利函數理論出現的古典效用主義的復興，並不是對古典效用主義的簡單回歸。如果說古典效用主義是在批判當時的天賦人權哲學、為新興資產階級的平等和自由思想提供理論基礎的話，那麼，現代的效用主義則是對現代資本主義發展過程中所出現的平等、正義等問題的進一步思考。現代資本主義的發展雖然在物質上取得了較大的成就，但是它所引發的許多社會道德問題反映出它對人文關懷的忽視所造成的嚴重後果。因此，現代的社會福利函數理論再度強調了平等、正義、福利等問題的重要性，再度強調了效率並不是一個社會所應追求的惟一目標。

　　另外，從現代西方社會福利函數理論的發展中我們還可以看到：現代社會福利函數理論乃至整個現代福利經濟學都和西方主流經濟學一樣有著不可剋服的天生的缺陷，這種缺陷並不因使用了高級的數學工具而有所剋服。這種缺陷就是：實證分析框架沒有充分考慮規範性的前提，實證分析和規範分析相互獨立。因此，真正剋服這種缺陷需要在發展規範分析的同時對整個主流框架進行重新審視和設立。