投資組合理論
出自 MBA智库百科(https://wiki.mbalib.com/)
投資組合理論(Portfolio Theory)
目錄 |
投資組合理論有狹義和廣義之分。狹義的投資組合理論指的是馬柯維茨投資組合理論Markowitz (1952) – about Portfolio Selection ;而廣義的投資組合理論除了經典的投資組合理論以及該理論的各種替代投資組合理論外,還包括由資本資產定價模型和證券市場有效理論構成的資本市場理論。同時,由於傳統的EMH不能解釋市場異常現象,在投資組合理論又受到行為金融理論的挑戰。
投資組合理論的提出[1]
美國經濟學家馬考維茨(Markowitz)1952年首次提出投資組合理論(Portfolio Theory),併進行了系統、深入和卓有成效的研究,他因此獲得了諾貝爾經濟學獎。
該理論包含兩個重要內容:均值-方差分析方法和投資組合有效邊界模型。
在發達的證券市場中,馬科維茨投資組合理論早已在實踐中被證明是行之有效的,並且被廣泛應用於組合選擇和資產配置。但是,我國的證券理論界和實務界對於該理論是否適合於我國股票市場一直存有較大爭議。
從狹義的角度來說,投資組合是規定了投資比例的一攬子有價證券,當然,單隻證券也可以當作特殊的投資組合。
人們進行投資,本質上是在不確定性的收益和風險中進行選擇。投資組合理論用均值—方差來刻畫這兩個關鍵因素。所謂均值,是指投資組合的期望收益率,它是單隻證券的期望收益率的加權平均,權重為相應的投資比例。當然,股票的收益包括分紅派息和資本增值兩部分。所謂方差,是指投資組合的收益率的方差。我們把收益率的標準差稱為波動率,它刻畫了投資組合的風險。
人們在證券投資決策中應該怎樣選擇收益和風險的組合呢?這正是投資組合理論研究的中心問題。投資組合理論研究“理性投資者”如何選擇優化投資組合。所謂理性投資者,是指這樣的投資者:他們在給定期望風險水平下對期望收益進行最大化,或者在給定期望收益水平下對期望風險進行最小化。
因此把上述優化投資組合在以波動率為橫坐標,收益率為縱坐標的二維平面中描繪出來,形成一條曲線。這條曲線上有一個點,其波動率最低,稱之為最小方差點(英文縮寫是MVP)。這條曲線在最小方差點以上的部分就是著名的(馬考維茨)投資組合有效邊界,對應的投資組合稱為有效投資組合。投資組合有效邊界一條單調遞增的凸曲線。
如果投資範圍中不包含無風險資產(無風險資產的波動率為零),曲線AMB是一條典型的有效邊界。A點對應於投資範圍中收益率最高的證券。
如果在投資範圍中加入無風險資產,那麼投資組合有效邊界是曲線AMC。C點表示無風險資產,線段CM是曲線AMB的切線,M是切點。M點對應的投資組合被稱為“市場組合”。
如果市場允許賣空,那麼AMB是二次曲線;如果限制賣空,那麼AMB是分段二次曲線。在實際應用中,限制賣空的投資組合有效邊界要比允許賣空的情形複雜得多,計算量也要大得多。
在波動率-收益率二維平面上,任意一個投資組合要麼落在有效邊界上,要麼處於有效邊界之下。因此,有效邊界包含了全部(帕雷托)最優投資組合,理性投資者只需在有效邊界上選擇投資組合。
50年代以前的投資組合理論[2]
在馬柯維茨投資組合理論提出以前,分散投資的理念已經存在。Hicks(1935)提出了“分離定理”,並解釋了由於投資者有獲得高收益低風險的期望,因而有對貨幣的需要;同時他認為和現存的價值理論一樣,應構建起“貨幣理論”,並將風險引入分析中,因為風險將影響投資的績效,將影響期望凈收入。 Kenes(1936)和Hicks(1939)提出了風險補償的概念,認為由於不確定性的存在,應該對不同金融產品在利率之外附加一定的風險補償,Hicks還提出資產選擇問題,認為風險可以分散。Marschak(1938)提出了不確定條件下的序數選擇理論,同時也註意到了人們往往傾向於高收益低風險等現象。Williams(1938)提出了“分散折價模型”(Dividend Discount Model),認為通過投資於足夠多的證券,就可以消除風險,並假設總存在一個滿足收益最大化和風險最小化的組合,同時能通過法律保證使得組合的事實收益和期望收益一致。Leavens(1945)論證了分散化的好處。隨後Von Neumann(1947)應用預期效用的概念提出不確定性條件下的決策選擇方法。
最優投資組合是指某投資者在可以得到的各種可能的投資組合中,唯一可獲得最大效用期望值的投資組合.有效集的上凸性和無差異曲線的下凸性決定了最優投資組合的唯一性。
馬柯維茨投資組合理論及其擴展[2]
馬柯維茨投資組合理論是美國經濟學家Markowitz(1952)發表論文《資產組合的選擇》,標志著現代投資組合理論的開端。他利用均值--方差模型分析得出通過投資組合可以有效降低風險的結論。
同時,Roy(1952)提出了“安全首要模型”(Safety-First Portfolio Theory),將投資組合的均值和方差作為一個整體來選擇,尤其是他提出以極小化投資組合收益小於給定的“災險水平”的概率作為模型的決策準則,為後來的VaR(Value at Risk)等方法提供了思路。
Tobin(1958)提出了著名的“二基金分離定理”:在允許賣空的證券組合選擇問題中,每一種有效證券組合都是一種無風險資產與一種特殊的風險資產的組合。
在Markowitz等人的基礎上,Hicks(1962)的“[[組合投資的純理論]”指出,在包含現金的資產組合中,組合期望值和標準差之間有線形關係,並且風險資產的比例仍然沿著這條線形的有效邊界這部分上,這就解釋了Tobin的分離定理的內容。Wiliam.F.Sharpe(1963)提出“單一指數模型”,該模型假定資產收益只與市場總體收益有關,從而大大簡化了馬柯維茨理論中所用到的複雜計算。
馬柯維茨的模型中以方差刻畫風險,並且收益分佈對稱,許多學者對此提出了各自不同的見解。
Mao(1970);Markowit(z1959);orter(1974);Hogan,Warren(1974);Harlow(1991)等認為下半方差更能準確刻畫風險,因此討論了均值一半方差模型。
Konno和Suzuki(1995)研究了收益不對稱情況下的均值-方差-偏度模型,該模型在收益率分佈不對稱的情況下具有價值,因為具有相同均值和方差的資產組合很可能具有不同的偏度,偏度大的資產組合獲得較大收益率的可能性也相應增加。Athayde,Flores(2002)考慮了非對稱分佈條件下的資產配置情況:在前兩階奇數矩限定的情況下,分別最小化方差與峰度並將其推廣到最小化任一奇數矩陣;Jondeau,Rockinger(2002)在投資者效用函數為常數相對風險厭惡(CRRA)效用函數的假定下將期末期望收益Taylor展開取前4階高階矩,運用一階條件來最優化資產配置;Jondeau,Rockinger(2005)考慮收益率的聯合非正態分佈和時變特征,包括了波動聚集性、非對稱和肥尾特征。將期末期望收益Taylor展開並取前4階高階矩,運用一階條件來最優化資產配置;Sahu等(2001,2003)提出偏正態分佈來衡量高階矩的影響,能充分考慮偏度與協偏度,同時處理“肥尾”的影響;Campbell R等(2004偏正態分佈估計高階矩的影響,貝葉斯方法處理收益分佈的參數不確定性情況,在上述基礎之上處理最優化問題。
Konno,Yamazaki(1991)用期望絕對偏差刻畫風險,建立了一個資產組合選擇的線性規劃模型,被稱為均值-絕對偏差模型。該模型如同均值-方差模型那樣也發展成均-下半絕對偏差模型;Young(1998)以資產組合收益的最小順序統計量作為風險度量利用極大極小規則建立了一個資產組合選擇的線性規劃模型;Cai(2000用資產組合項資產收益中的最大期望絕對偏差來刻畫風險,建立了一個資產組合選擇的線性規劃模型並給出瞭解析解。
投資組合理論的主要內容[3]
馬克維茨投資組合理論的基本假設為:(1)投資者是風險規避的,追求期望效用最大化;(2)投資者根據收益率的期望值與方差來選擇投資組合;(3)所有投資者處於同一單期投資期。馬克維茨提出了以期望收益及其方差(E,δ2)確定有效投資組合。
以期望收益E來衡量證券收益,以收益的方差δ2表示投資風險。資產組合的總收益用各個資產預期收益的加權平均值表示,組合資產的風險用收益的方差或標準差表示,則馬克維茨優化模型如下:
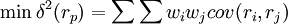
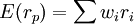
式中:rp——組合收益;
ri、rj——第i種、第j種資產的收益;
wi、wj——資產i和資產j在組合中的權重;
δ2(rp)——組合收益的方差即組合的總體風險;
cov(r,rj)——兩種資產之間的協方差。
馬克維茨模型是以資產權重為變數的二次規劃問題,採用微分中的拉格朗日方法求解,在限制條件下,使得組合風險鏟δ2(rp)最小時的最優的投資比例Wi。從經濟學的角度分析,就是說投資者預先確定一個期望收益率,然後通過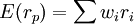 確定投資組合中每種資產的權重,使其總體投資風險最小,所以在不同的期望收益水平下,得到相應的使方差最小的資產組合解,這些解構成了最小方差組合,也就是我們通常所說的有效組合。有效組合的收益率期望和相應的最小方差之間所形成的曲線,就是有效組合投資的前沿。投資者根據自身的收益目標和風險偏好,在有效組合前沿上選擇最優的投資組合方案。
確定投資組合中每種資產的權重,使其總體投資風險最小,所以在不同的期望收益水平下,得到相應的使方差最小的資產組合解,這些解構成了最小方差組合,也就是我們通常所說的有效組合。有效組合的收益率期望和相應的最小方差之間所形成的曲線,就是有效組合投資的前沿。投資者根據自身的收益目標和風險偏好,在有效組合前沿上選擇最優的投資組合方案。
根據馬克維茨模型,構建投資組合的合理目標是在給定的風險水平下,形成具有最高收益率的投資組合,即有效投資組合。此外,馬克維茨模型為實現最有效目標投資組合的構建提供了最優化的過程,這種最優化的過程被廣泛地應用於保險投資組合管理中。
馬克維茨投資組合理論的基本思路是:(1)投資者確定投資組合中合適的資產;(2)分析這些資產在持有期間的預期收益和風險;(3)建立可供選擇的證券有效集;(4)結合具體的投資目標,最終確定最優證券組合。
資本資產定價模型及其擴展[2]
馬柯維茨投資組合理論之後,Sharpe(1964),Lintner(1965),Mossin(1966)分別提出了各自的資本資產定價模型(CAPM)。這些模型是在不確定條件下探討資產定價的理論,對投資實踐具有重要的指導意義。
資本資產定價模型提出之後,研究者進一步擴展了該研究。
Jensen Michael(1969)提出以CAPM中的證券市場線為基準來分析投資組合績效的非常規收益率資本資產定價模型,但由於在非系統風險不能完全剔除的情況下,該模型對投資組合績效的評價結果不如CAPM的評價結果,因此該模型在實際中應用不多。
Brennan(1970)提出了考慮稅率對證券投資報酬影響的資本資產定價模型;Vasicek,(1971),Black(1972)分別研究了不存在無風險借貸時的資本資產定價模型;Mayers(1972)提出了考慮存在退休金、社會保險等非市場化資產情況下的資產定價模型的建立;Merton(1973)提出了多因素的ICAPM模型 (Intertemporal CAPM),為後來的長期投資理論奠定了基礎。E.Linderberg(976、1979)研究了存在價格影響者時的資本市場均衡和投資者的組合選擇問題。結果發現所有投資者(包括價格影響者)都持有市場組合和無風險資產的某個組合,故仍可得到形式簡單的CAPM,只不過此時的單位風險價格低於所有投資者都是價格接收者時的單位風險價格。他還證明瞭通過兼併或合伙,個體或機構投資者可以增加他們的效用,這就是大型金融機構存在的原因之一。
Sharpe(1970),E.Fama(1976),J.Lintler(1970),N.J.Gonedes(1976)等分別研究了投資者對資產將來的期望收益、收益的方差、協方差期望不一致時資本市場的均衡,他們得到了形式於標準CAPM類似的CAPM。
由於資本資產定價模型的假設條件過於嚴格,使其在應用中受到一定局限。因此,對於CAPM的突破成為必然。
Stephen.A.Ross(1976)提出了套利定價理論(APT)。APT不需要像CAPM那樣作出很強的假定,從而突破性地發展了CAPM。
Black,Scholes(1973)推導出期權定價公式,即B一S模型;Merton(1973)對該定價公式發展和深化。針對B—S模型假定股票價格滿足幾何--布朗運動在大多數情況下不符合實際價格變化的問題,Scholes,Ross(1976)在假定股票價格為對數泊松發佈情況下推導出了純跳空期權定價模型(Pure Jump Model);Merton(1976)提出了擴散--跳空方程(Diffusion-Jump Model);格利斯特和李(1984)研究了基礎證券交易成本對期權價值的影響:當存在交易成本時,連續時間無套利定價會因為高昂的交易成本而無法實現;Merton(1990)運用了離散時間模型提出了交易成本與基礎證券價格成比例的單階段期權定價公式;波耶勒和沃爾斯特(1992)將Merton 的方法推廣到了多階段情形。
拉馬斯瓦米,桑達瑞森(1985);Brenner;科塔頓,薩布拉曼·彥(1985)以及貝爾和托羅斯(1986)的研究指出,美式期貨期權在利率為正的條件下比美式現貨期權更易於執行;Lieu(1990)應用連續時間定價方法推出了期貨純期權的定價公式;陳,斯科特(1993)進一步研究指出,即使利率是隨機的,期貨純期權價值也不受利率的影響;Chaudhurg,Wei(1994)研究了常規期貨期權與純期權的價值關係,指出期貨純期權的價值高於美式期貨期權的價值。Harrison,Krep(1979)發展了證券定價的鞅理論(theory of martingale pricing),該理論目前仍是金融研究的前沿課題。
現代投資理論的產生與發展[1]
現代投資組合理論主要由投資組合理論、資本資產定價模型、APT模型、有效市場理論以及行為金融理論等部分組成。它們的發展極大地改變了過去主要依賴基本分析的傳統投資管理實踐,使現代投資管理日益朝著系統化、科學化、組合化的方向發展。
1952年3月,美國經濟學哈里·馬考威茨發表了《證券組合選擇》的論文,作為現代證券組合管理理論的開端。馬克威茨對風險和收益進行了量化,建立的是均值方差模型,提出了確定最佳資產組合的基本模型。由於這一方法要求計算所有資產的協方差矩陣,嚴重製約了其在實踐中的應用。
1963年,威廉·夏普提出了可以對協方差矩陣加以簡化估計的夏普單因素模型,極大地推動了投資組合理論的實際應用。
20世紀60年代,夏普、林特和莫森分別於1964、1965和1966年提出了資本資產定價模型(CAPM)。該模型不僅提供了評價收益-風險相互轉換特征的可運作框架,也為投資組合分析、基金績效評價提供了重要的理論基礎。
1976年,針對CAPM模型所存在的不可檢驗性的缺陷,羅斯提出了一種替代性的資本資產定價模型,即APT模型。該模型直接導致了多指數投資組合分析方法在投資實踐上的廣泛應用。
投資組合的思想[1]
1、傳統投資組合的思想——Native Diversification
(1)不要把所有的雞蛋都放在一個籃子裡面,否則“傾巢無完卵”。
(2)組合中資產數量越多,分散風險越大。
2、現代投資組合的思想——Optimal Portfolio
(1)最優投資比例:組合的風險與組合中資產的收益之間的關係有關。在一定條件下,存一組在使得組合風險最小的投資比例。
(2)最優組合規模:隨著組合中資產種數增加,組合的風險下降,但是組合管理的成本提高。當組合中資產的種數達到一定數量後,風險無法繼續下降。
3、現代投資理論主要貢獻者(Pioneers):
貢獻者 簡介 主要貢獻 代表作(Classic Papers) 托賓(James Tobin) 1981年諾貝爾經濟學獎,哈佛博士,耶魯教授。 流動性偏好、托賓比率分析、分離定理。 “Liquidity Preference as Behavior toward Risk,” RES,1958. 馬考維茨(Harry Markowitz) 1990年諾貝爾經濟學獎,曾在蘭德工作。 投資組合優化計算、有效疆界。 “Portfolio Selection,”,JOF,1952. 夏普(William Sharp) 1990年諾貝爾經濟學獎,曾在蘭德工作,UCLA博士,華盛頓大學、斯丹福大學教授。 CAPM “Capital Asset Pricing: A Theory of Market Equilibrium Under Condition of Risk,” JOF, 1964. 林特勒(John Lintner) 美國哈佛大學教授 CAPM “The Valuation of Risk Assets & Selection of Risky Investments in Stock Portfolio & Capital Budget,” RE&S, 1965.
投資組合的基本理論[1]
馬考維茨經過大量觀察和分析,他認為若在具有相同回報率的兩個證券之間進行選擇的話,任何投資者都會選擇風險小的。這同時也表明投資者若要追求高回報必定要承擔高風險。同樣,出於迴避風險的原因,投資者通常持有多樣化投資組合。馬考維茨從對回報和風險的定量出發,系統地研究了投資組合的特性,從數學上解釋了投資者的避險行為,並提出了投資組合的優化方法。
一個投資組合是由組成的各證券及其權重所確定。因此,投資組合的期望回報率是其成分證券期望回報率的加權平均。除了確定期望回報率外,估計出投資組合相應的風險也是很重要的。投資組合的風險是由其回報率的標準方差來定義的。這些統計量是描述回報率圍繞其平均值變化的程度,如果變化劇烈則表明回報率有很大的不確定性,即風險較大。
從投資組合方差的數學展開式中可以看到投資組合的方差與各成分證券的方差、權重以及成分證券間的協方差有關,而協方差與任意兩證券的相關係數成正比。相關係數越小,其協方差就越小,投資組合的總體風險也就越小。因此,選擇不相關的證券應是構建投資組合的目標。另外,由投資組合方差的數學展開式可以得出:增加證券可以降低投資組合的風險。
基於迴避風險的假設,馬考維茨建立了一個投資組合的分析模型,其要點為:
(1)投資組合的兩個相關特征是期望回報率及其方差。
(2)投資將選擇在給定風險水平下期望回報率最大的投資組合,或在給定期望回報率水平下風險最低的投資組合。
(3)對每種證券的期望回報率、方差和與其他證券的協方差進行估計和挑選,併進行數學規劃(mathematicalprogramming),以確定各證券在投資者資金中的比重。
投資組合理論的新發展[2]
(一)基於交易費用和流動性的投資組合理論
如果市場是無效的和存在摩擦的,就會導致交易成本的存在,而開放式基金的流動性直接與交易成本相關。關於市場摩擦的投資組合問題,是由Magil和 Constantinides首先提出來的,之後Davis和Norman對此做了進一步研究。Davis(1990)等人利用隨機控制方法分析了在存在市場摩擦的情況下與證券流動性相關的交易成本問題,發現保持在一定風險區間內並且在接近區間的邊界時作最小交易是合理的。 Shreve,Akian(1995)等人利用粘度理論研究了具有交易成本的多維資產組合問題,並利用有限差分法求解了一個三資產的期終財富最大化問題。但是,Davis,Shreve,Akian等提出的方法忽略了固定成本所導致的較大交易成本,後來的Eastham和Hastings使用脈衝控制方法有效地解決了這一問題。Morton和Pliska(1995)也研究了固定交易成本下的最優組合管理問題,儘管他們建立的模型中的交易成本不是真實的交易成本,但是他們的方法在解決相應的組合問題時具有一定的指導作用。
最近的研究認為證券的流動性是證券價值的決定性因素,相對於流動性證券來說,非流動性證券的定價總是存在一定的折扣。例如Amihud和 Mendelson(1991),Kamara(1994)就證實在非流動性的中期債券和流動性的國債間存在超過35個基本點的收益差距;Whitelaw(1991)等也證實過類似現象。Brito(1977),Subrahanyam (1979),Amihud和Mendelson(1986),Duma,和Luciano(1991),Boudoukh和 Whitelaw(1993),Constantinides和Mehra(1998)等關於資產組合的流動性作用的研究成果,集中在外生的交易成本和借入或賣出的限定上,而後來Longstaf(2001)的研究則是集中於交易策略和證券價值內生的非流動性作用上。Longstaf解決了投資者受限於流動性限制的跨期組合問題。
(二)基於風格投資的投資組合理論
風格投資始於1992年威廉·夏普的論文《資產配置:風格管理與業績評價》。風格投資在國外的研究主要集中在以下幾方面:
第一,投資風格的分析。目前普遍接受的風格分析方法主要有和基於組合的風格分析。前者是由Sharp提出基於收益的風格分析,他認為通過比較基金的收益和所選擇的風格指數收益之間的關係可以判定基金管理人在過去一段時間的投資風格;後者主要是根據基金實際持有的股票特征來劃分基金的投資風格。 Kahn(1996)發現對於小樣本基金,基於組合分析來預測風險比基於收益的分析方法具有更高的相關性;Kaplan(2003)研究發現對於大盤價值型組合,兩種風格分析方法所得結果相似,而對於中小盤和成長型組合,兩種分析方法則存在顯著差異。
第二,風格投資的表現及形成原因研究。風格投資常常表現出小市值效應(投資於小規模公司股票所獲得的收益要高於投資於大規模公司股票)和BV/MV效應(凈資產/市值)。Banz(1981)最早發現,最小一類公司股票的平均收益率要高出最大一類股票19.8%;Reinganum (1981)也發現類似現象。對於BV/MV效應,Stattman (1980)發現美國公司股票的平均收益與其BV/MV呈正相關關係;Fama和French(1992)也證明美國市場的BV/MV效應明顯。對此,有這樣幾種解釋:其一,Fama和French(1993,1995),Johnson(1997)等人認為風格投資的超額收益是對風險的補償,而這些風險被正統的資本資產定價模型所遺漏;其二,Lakonishok,Shleifer和Vishny(1994)認為超額收益是由於投資者對某種股票過去表現的過度反應所致;其三,Daniel和Titman(1997)認為由於具有某種相同屬性的公司分享著某些共同特征,因而有可能同時出現一些經營上的問題而導致上述兩種效應;其四認為是計算方法的選擇以及數據處理等人為原因造成的。
第三,風格投資的周期性以及風格轉換策略研究。從價值型/成長型或大盤股刊、盤股等角度來看,風格投資在不同時期有著不同表現,存在周期性。弗蘭克等 (2002)研究表明,美國、日本股票市場中小盤股/大盤股總是間隔表現較差或優良。David,Robert和Christopher (1997)通過美國、加拿大等國數據分析發現,價值型/成長型組合的收益率存在較為明顯的周期型。由於風格投資具有周期性,因而投資者可以通過風格轉換以獲取更好收益。Levi,和Liodakis(1999)通過對英國股市的研究認為,當兩種相對風格的收益率差異不顯著時,投資者有機會通過風格轉換增進組合績效;另外一些學者如KevinQ .W ang(2003)、Georgi(2003)等也分別對此現象進行了研究。
第四,風格投資對證券市場的影響研究。Lee和Andrei等(1991)用風格投資的理論解釋了為什麼在同一證券市場掛牌的基金雖持有完全不同的股票,但卻同漲同跌;Froot等(1999)同樣運用風格投資的概念解釋了在不同交易所上市的同種股票卻有著不同表現的原因;Sorensen與 Lazzara(1995),Anderrson(1997)及Fochtman(1995)也先後就某種風格與某種具體影響因素(如巨集觀經濟因素、價格趨勢等)之間的關係進行了研究。
(三)基於連續時間的長期投資組合理論
長久以來,馬柯維茨的均值--方差理論在指導人們短期投資中占有重要地位。但事實上,長期投資和短期投資的最優資產組合不盡相同。
Samuelson(1963,1969)等最早描述了長期投資者與短期投資者作出相同決策的限制條件;Merton(1969,1971,1973)也對此進行了長期、深人的研究。他們的研究告訴人們,投資機會會隨時間變化,長期投資者總是關心長期中投資機會所受到的衝擊,並希望從中套利。 Kim,Omberg(1996);Balduzzi;Lynch(1999);Barberis(2000)等人建立了長期投資者資產組合選擇的實證模型,這些模型是建立在 Samuelson(1963,1969);Mossin(1968);Merton(1969,1971,1973);Stiglitz(1979);Rubinstein(1976a,b);Breeden(1979)等文獻的基礎上,並且最終完成了早期理論文獻的實證檢驗。他們假設一個生命有限的投資者具有期末財富的HARA (hyperbolic absolute risk aversion)效用,結果發現沒有用到任何近似,最優的組合權重是線性的。Balduzzi,Lynch通過對那些忽視投資長期性的投資者的效用檢驗得出,忽略現實的交易成本將導致效用成本增加0.8%到16.9%;Barberis研究發現即使將許多參數的不確定性包含進模型之後,還有足夠的收益期望使長期投資者總能在股票上分配更多資產。
對於利率在長期的影響,Morton(1973)提出了套期保值效應,當投資者的風險厭惡繫數大於1時,對風險資產的需求不僅受到資產風險溢價的影響,還受到預期收益率與預期遠期利率調整的協方差的影響;對於跨期理論中的跨期預算約束條件,Campbel(1993)認為當消費--財富比率不變或變動不大時,投資者的跨期預算約束條件為近似線形;Tepla(2000)在允許借入和賣空的約束條件下,將靜態投資組合的選擇標準結果擴展到動態的跨期模型。 Campbell和Viceira(2001)對這部分結論也有詳細的闡述。
對長期投資的資產組合選擇和風險控制問題,Jeremy Siegel(1994)通過分析認為在長期投資中,股票的風險低於債券甚至國庫券,在長期股票是最安全的投資資產。 Campbel,Viceira(1999,2000)證明對最優投資策略中市場擇機的忽略,會導致更大的效用損失。 Campbell,Chan,Viceira (2001)等用VaR(一階向量自回歸)模型來分析長期投資者的消費和資產組合選擇問題。研究表明,股票收益的可預測性增加了投資者對於股票投資的需要,並且長期通貨膨脹債券能夠增加穩健投資者的效用; John Y.Campbell,George Chacko,Jorge Rodriguez(2004)的研究也展示,保守的長期投資者有一個積極的股票跨期套利需求。這些研究對長期資產組合框架的建立作出了卓越貢獻。
對長期投資的資產配置問題,用連續時間數學來分析動態資產組合選擇,至少可以追溯到Robert Merton(1969--1973)的研討工作。Duffle(1996);Karatzas,Shreve(1998);Morton(1990)給出了連續時間中資產組合選擇的一般方法。Chacko,Viceira(1999)探討了時變風險對投資的影響。 Cox,Huang(1989);Cox,Leland(1982);Pliska(1996)等提出跨期消費與資產組合選擇的“鞍方法”,利用完全市場中的SDF(隨機貼現因數)屬性,把動態問題轉換為靜態問題,使得結果更容易求解。Campbell,Viceira(2002)在他們合著的《戰略資產配置:長期投資者的資產組合選擇》中第一次系統地討論了長期資產組合選擇問題。他們創立了一個可以與均值方差分析相媲美的跨期實證分析方法;證明瞭長期通貨膨脹指數化債券是對於長期投資者的無風險資產;揭示了股票作為對長期投資者比短期投資者更為安全資產的條件;證明瞭勞動收入怎樣影響資產組合選擇。
(四)基於VaR的投資組合理論
VaR方法在20世紀50年代才得到研究證券投資組合理論的學者們關註,它原先被人們用於測度一些金融公司交易證券的市場風險。VaR方法的引入在一定程度上彌補了原先投資組合理論對證券投資組合風險度量的不足。
國外學者先後給VaR從不同角度進行定義。
Joroin(1996)認為是給定概率置信水平內最壞情況下的損失;Sironi,Resti(1997)認為是在定義期間內,在一定的概率條件下,潛在的最大損失。
Luciano(1998)認為是在一定的概率條件下,單個頭寸或整個組合可能產生的損失;在給定資產(組合)價值變動分佈的前提下,風險按照價值變動超過某一臨界點的可能性來界定。
Mauser,Rosen,Jorion(2001)分別利用歷史模擬法或蒙特卡羅模擬法估算了VaR條件下的資產組合選擇最優化問題。但VaR仍然存在有很多的缺陷。
Artzner等(1999)提出了一致性風險度量(Coherent Measures of Risk)的概念,其中一致性以四條公理假設條件作為判別標準,由於VaR不滿足四個條件中的次可加性(Sub-Additivity),意味著在某些條件下拒絕資產組合風險分散化原理,認為VaR不是一個Coherent風險度量。
基於此,Pflug,Rockafellar,Uryasev(2000,2002);Acerbi,Tasche(2002)先後提出了條件風險價值(Conditional Valueat Risk,CVaR)作為風險的度量來對VaR進行修正。CvaR被定義為損失超過VaR部分的條件期望,只考慮下跌風險(Downside Risk)。如果VaR對應的置信區間為(1-α),則α-CVAR就是超過α-VAR的平均損失;針對VaR無法比較來自不同市場的風險暴露,Giuseppe Tardivo(2002)提出Benchmark-VaR的概念,即在一定的時間段內,在一定的置信區間內,基金或者組合偏離基準(Benchmark)的最大離差;Emmer等(2001)引入了風險資本(Capital at Risk,CaR)的概念,用以代替方差來衡量風險;鑒於VaR僅測度了市場常態下的資產組合的風險,Embrechts等(1997)將測度極端情況的極值理論與VaR相結合提出了測度市場極端風險的方法,McNeil,Frey(2000)運用極值理論研究了瑞士金融市場時間序列的尾部特征,結論認為極值方法比VaR更為穩健和精確。
在界定了VaR和CVaR等風險測度指標後,以其為基礎研究資產組合選擇的工作相應展開。
Rockafellar等(2000),Anderson等(2001)考慮了CVaR作為風險測度時的資產組合優化問題,證明瞭CVaR是凸函數,可以用來構建有效的優化方法,而且Rockafellar等還提出了一種線性規劃方法,可以同時最小化VaR和CVaR。Emmer等在引入了風險資本(Capital at Risk,CaR)的概念後,建立了資產組合選擇的“均值-CaR模型”,推導出解析形式的最優解和有效邊界;Young(1998)提出了一個極大極小收益的資產組合模型(MMR):在保證資產組合平均收益率超過某一最低收益水平約束下,極大化其任一時期的極小收益,決策目標是考慮在最不利收益中取最優收益。風險度量指標採用的是最小的可能收益而不是方差。
另外Bogentoft等(2001);Topaloglou等(2002);Castellacci,Siclari(2003)也研究了基於VaR和CVaR的資產組合選擇問題。
(五)基於非效用最大化的投資組合理論
Cover是較早非效用最大化投資組合理論的學者之一,他提出了在離散時間條件下的泛組合模型。該模型的突出優點是構建它不需要知道市場參數及有關統計信息,如利率、價格波動率,甚至不需要詳細描述離散時間條件下價格變動的動力學機制,只要通過跟蹤不同證券權重的績效加權變動情況便可達到最優恆定組合。 Cover還描述了泛組合的漸近行為,並引用實例說明瞭泛組合具有較好的解釋力。
Hellwing提出了一種普遍適用的經濟資源定價方法---價值維持原理(Value Preserving Principle),即資源的內在價值(將來收益價值)不隨時間變化而變化。Helwing利用該方法考察了在離散時間、有限狀態空間條件下證券市場的組合最優化問題,並表現出較好的解釋力。
Buckley和Korn從考察隨機現金流下的指數跟蹤誤差的角度認為:對於那些消極跟蹤指數的投資者來說,其理想狀況的證券組合總是由進人指數的所有證券持有組成。這必然導致資本資產投資者持有的現金賬戶績效與指數績效的偏離(即導致跟蹤誤差的產生)。據此,Buckley和Korn給出了這種情形下的相關模型(即基於半鞍的一般連續時間模型),分析了投資者導致的脈衝控制問題,並給出了其存在最優控制策略的一般條件。除此之外,他們還探討了某些擴散類型市場價值維持策略的存在性和惟一性,解決了來自於非完全市場中的期權套期保值理論的惟一價值維持測度問題(即最小鞍測度問題),並考察了附加約束對組合策略的影響。
(六)行為金融和行為投資組合理論
近20年來的金融實證研究不斷發現股票收益率具有可預測性的證據,EMH的理論基礎和實證檢驗都受到了強有力的挑戰。證券市場上實證研究發現了許多無法由 EMH和資本資產定價模型加以合理解釋的異常現象。面對一系列金融異象,人們開始質疑以有效市場假說為核心的傳統金融理論。由於行為金融學能夠較好地解釋這些現象,因此原先不受重視的行為金融學開始受到越來越多學者的關註。
行為金融學的發展可分為三個階段:
第一,萌芽階段。
行為金融學的起源可追溯到19世紀Gustave Lebon和Mackey[1]在其著作中就已經開始研究投資市場行為了。凱恩斯(1936年)的“空中樓閣理論”開始關註投資者自身的心理影響。該理論主要從心理因素角度出發,強調心理預期在人們投資決策中的重要性。他認為決定投資者行為的主要因素是心理因素,投資者是非理性的,其投資行為是建立在所謂“空中樓閣”之上,證券的價格決定於投資者心理預期所形成的合力,投資者的交易行為充滿了“動物精神”(animal spirit)。
Burrel(1951)發表《投資戰略的實驗方法的可能性研究》一文,標志著行為金融學的真正產生,該文首次將行為心理學結合在經濟學中來解釋金融現象。
第二,基礎理論確立階段。
Burrel,Bauman(1969)發表《科學投資方法:科學還是幻想》認為,金融學新的研究領域應該重點考慮數量模型和傳統行為方法的結合,這樣會更貼近實際。
Slovic,Bauman教授(1972)發表了《人類決策的心理學研究》,這篇文章為行為金融學理論作出了開創性的貢獻。
Daniel Kahneman,Amos Tversky(1974)在《科學》雜誌中,討論了直覺驅動偏差(Heuristic-driven error)。
Tversky,Kahneman(1979)發表了《展望理論:風險決策分析》,正式提出了展望理論。該理論以其更加貼近現實的假設,嚴重衝擊並動搖了傳統金融學所依賴的期望效用理論,併為行為金融學奠定了堅實的理論基礎。
同時,Tversky,Kahneman(1979)在《經濟計量學雜誌》討論了框架依賴(Frame dependence)。
第三,發展繁榮階段。
預期理論的提出大大推動了行為金融學的發展,一大批研究成果相繼取得。
Debondt,Thaler(1985)發表了題為《股票市場過度反應了嗎?》一文,引發了行為金融理論研究的復興。
De Bondt,Thaler(1985,1987)發現的逆向投資策略以及Jegadeesh,Titmann(1993,2001,2002)發現的動量投資策略,更是引起市場的廣泛關註。而Robert Shearer(2000)發表的《非理性繁榮》卻標誌行為金融學的興起。
De Bondt(2000)實證研究發現除了美國之外,英國、加拿大、德國、瑞士、瑞典、荷蘭、西班牙、馬來西亞、澳大利亞、巴西等國家都存在過度反應現象。與過度反應情況相反,Jegadeesh,Titman(1993)發現,根據過去3--12個月的市場表現,買進表現較好的公司股票,同時賣出表現較差的公司股票,所構造的這個零投資組合在下一年度平均每月有1%的收益。Rouwenhorst(1998)採用1978--1995年間歐盟12國的 2190家公司作為樣本構造國際投資組合。在考慮了風險、公司規模、不同國家差異後,實證研究結果表明,過去贏家在未來1年內的表現優於過去的輸家大約每月1%。這個結果與Jegadeesh,Titman(1993)關於美國市場的結果是一致的。
針對上述問題,出現了許多解釋性的研究結果。
Zarowin(1990)認為逆向效應可能是季節效應造成的。Conrad,Kaul(1998)將動量投資策略和逆向投資策略的獲利性完全歸因於期望收益率的截面方差,而不是任何收益率可測的時間序列方差。 Barberis,Shleifer,Vishny(1998);Daniel,Hirshleifer,Sburamanyam(1998);Hong Stein(1999);Huang,Barberis(2001)認為行為金融理論所描述的投資者解讀信息方式的內在偏差或信息緩慢擴散也可能導致所謂股價反應不足和過度反應,從而產生逆向效應和動量效應。Moskowitz,Grinblatt(1999)認為個股動量效應可以由行業動量效應來解釋。
Lo,Mackinlay(1990a)以及Jegadeesh,Titman(1995)認為股價對信息反應不足或者反應過度是導致投資組合內個股自身及彼此間收益率時間序列可預測性的原因,也是動量投資策略和逆向投資策略獲利性的重要來源。Barberis(1998)提供了可解釋反應過度和反應不足的模型。Hersh Shefrin(2000)提出情緒測度的概念,以情緒測度資產價格和基本價值之間的總體偏差。異質能解釋期權定價的“波動性微笑”和均值方差組合的“皺眉”。Mehra,Sah(2002)在Becker,Mulligan(1997)建立的主觀貼現因數內生決定的理論框架基礎上將主觀貼現因數的波動稱為情緒波動,併進一步研究了主觀貼現因數的波動對均衡股票價格的定量影響。他們通過計算發現,主觀貼現因數的1個百分點的波動可以導致股票價格高達幾十個百分點的波動。也就是說,投資者情緒的較小波動,可以引起股票價格的很大波動。從而解釋了股票市場的過度波動性。
在行為金融繁榮發展的過程中,行為金融學有關理論和行為資產組合理論(BPT)及行為資產定價模型(BAPT)也在迅速發展。
Shiller(1989)從證券市場的波動性角度,揭示出投資者具有非理性特征,同時他在羊群效應、投機價格和流行心態的關係等方面也做出了卓著的貢獻。
Odean(1998)考察了行為金融的處置效應---持有劣質東西而賣出優質東西的傾向。
Poterba(1998)說明終身捐贈是和行為金融直接相關的。
Thaler(1987,1999)研究了股票回報率的時間序列、投資者“心理賬戶”以及“行為生命周期假說”等問題。
Rabin(2001)將人的心理行為因素引入經濟學的分析模型,他關註在自我約束的局限下,人們會出現“拖延”和“偏好反轉”等行為,這些有趣的研究成果對儲蓄、就業等問題都具有一些有意義的啟示。
Belsky,Gilovich(1999);Shefrin(2000)很好地介紹了行為金融,後者更加翔實。
Barber,Odean,Zheng(2005)透視了共同基金投資者支出的重要性和行為金融概念的框架,強調瞭如何傳遞信息才能使信息和其內容一樣重要。
Delong,Shleife(1990)研究了不可預測的隨機交易的結果,說明噪音交易者的隨大流買賣導致了溢價的波動。
Shefrin,Statman(1994)構造了一個關於異質交易者的對數效用函數模型,他們分析了代表人怎樣利用不同交易者的異質理念,指出異質造成短期利率是隨機而非固定的。Cabrales,Hoshi(1996)給出一個關於異質理念的動態定價模型。
Shefrin,Statman(1994)以Roy(1952)的安全第一模型和Lopes(1987)的SP/A理論為基礎,將投資者行為的研究成果與資產組合選擇模型結合起來,提出單一心理賬戶行為資產組合理論(BPT-SA)。該理論建模類似於均值-方差模型,目標函數也是期末財富期望值最大化,不同在於它的約束條件:期末財富低於最低財富的概率水平低於事前設定值。Shefrin,Statman還進一步提出多心理賬戶行為資產組合選擇理論(BPT-MA)。
Gul(1991)建立一個考慮投資者失望厭惡效用函數模型,併進行了公理性的證明工作;利用他的研究工作,Epstein,Wang(1994);Bekaert等(1997)研究均衡資產定價問題;Ang等(2000)分析了失望厭惡偏好投資者的資產組合選擇問題,得出一些定性的結論。Hwang,Satchell(2001)利用Benartzi,Thaler(1995)的損失厭惡效用函數模型分析了資產組合選擇問題。他們的研究表明由於失望厭惡和損失厭惡的存在,投資者在面臨不利投資環境和事實損失時將更加趨向於風險厭惡,從而資產配置向無風險資產傾斜。
Daniel等(2001)研究了過度自信的投資者和風險厭惡的理性套利者相互交易的多種風險證券的過度自信模型。
在行為資產定價理論方面,Epstein,Zin(1989,1991);Weil(1989,1990)在Kreps,Porteus(1978)的理論框架基礎之上提出了更加靈活的遞歸效用函數,推廣了傳統的時間可分、狀態可分效用函數。而Weil(1989),Campbell(1999)在研究股票溢價之謎和無風險利率之謎時;Smith(2001);Seckin(2000);Campbell(1993);Restoy,Weil(1998);Duffie,Epstein(1992)研究資產定價模型時;Svensson(1989);Weil(1990);Dumas,Uppal,Wang(2000);Schroder,Skiadas(1999) 時將遞歸效用函數應用到資產定價領域的研究工作中。
Constantinides(1990)在Merton(1969,1971)基礎之上求解了引入習慣的消費-投資組合模型,並使用最優解解釋了股票溢價之謎和消費平滑之謎。Sundaresan(1989)研究了基於習慣形成的資本資產定價模型。Abel(1990)使用習慣形成解釋了股票溢價之謎。 Carroll(2000);Campbell,Cochrane(1999);Campbell(2000)研究了習慣形成對資產定價的影響。 Ferson,Constantinides(1991);Boldrin,Christiano,Fisher(1997);Haug(2001);Li(2001) 也研究了習慣形成對資產價格的影響。
Abel(1990)研究了基於追趕時髦的資產定價模型。Gali(1994),Gollier(2003)研究了基於嫉妒的資產定價模型。 Abel(1999)構造了一個基於嫉妒和追趕時髦的消費外在性基礎上的效用函數,並研究了一般均衡下資產的風險溢價和期限溢價。
Bakshi,Chen(1996a)首次研究基於財富偏好的資產定價理論,在Merton(1969,1971)基礎之上求解了基於消費偏好的消費-投資組合模型,並得到了相應的資產定價模型。
Barberis,Huang,Santos(2001)在Lucas(1978)基礎上,將投資者的效用函數定義在消費和財富的波動之上,從而投資者不但規避消費風險,還規避財富的損失
Brunel(2005–2006,2006),Chhabra(2005),Nevin(2004)研究了行為資產配置。
投資組合理論的應用[1]
投資組合理論為有效投資組合的構建和投資組合的分析提供了重要的思想基礎和一整套分析體系,其對現代投資管理實踐的影響主要表現在以下4個方面:
1.馬考威茨首次對風險和收益這兩個投資管理中的基礎性概念進行了準確的定義,從此,同時考慮風險和收益就作為描述合理投資目標缺一不可的兩個要件(參數)。
在馬考威茨之前,投資顧問和基金經理儘管也會顧及風險因素,但由於不能對風險加以有效的衡量,也就只能將註意力放在投資的收益方面。馬考威茨用投資回報的期望值(均值)表示投資收益(率),用方差(或標準差)表示收益的風險,解決了對資產的風險衡量問題,並認為典型的投資者是風險迴避者,他們在追求高預 期收益的同時會儘量迴避風險。據此馬考威茨提供了以均值一方差分析為基礎的最大化效用的一整套組合投資理論。
2.投資組合理論關於分散投資的合理性的闡述為基金管理業的存在提供了重要的理論依據。
在馬考威茨之前,儘管人們很早就對分散投資能夠降低風險有一定的認識,但從未在理論上形成系統化的認識。
投資組合的方差公式說明投資組合的方差並不是組合中各個證券方差的簡單線性組合,而是在很大程度上取決於證券之間的相關關係。單個證券本身的收益和標準 差指標對投資者可能並不具有吸引力,但如果它與投資組合中的證券相關性小甚至是負相關,它就會被納入組合。當組合中的證券數量較多時,投資組合的方差的大 小在很大程度上更多地取決於證券之間的協方差,單個證券的方差則會居於次要地位。因此投資組合的方差公式對分散投資的合理性不但提供了理論上的解釋,而且 提供了有效分散投資的實際指引。
3.馬考威茨提出的“有效投資組合”的概念,使基金經理從過去一直關註於對單個證券的分析轉向了對構建有效投資組合的重視。
自50年代初,馬考威茨發表其著名的論文以來,投資管理已從過去專註於選股轉為對分散投資和組合中資產之間的相互關係上來。事實上投資組合理論已將投資管理的概念擴展為組合管理。從而也就使投資管理的實踐發生了革命性的變化。
4.馬考威茨的投資組合理論已被廣泛應用到了投資組合中各主要資產類型的最優配置的活動中,並被實踐證明是行之有效的。
馬考威茨的投資組合理論不但為分散投資提供了理論依據,而且也為如何進行有效的分散投資提供了分析框架。但在實際運用中,馬考威茨模型也存在著一定的局限性和困難:
1.馬考威茨模型所需要的基本輸入包括證券的期望收益率、方差和兩兩證券之間的協方差。當證券的數量較多時,基本輸入所要求的估計量非常大,從而也就使得馬考威茨的運用受到很大限制。因此,馬考威茨模型目前主要被用在資產配置的最優決策上。
2.數據誤差帶來的解的不可靠性。馬考威茨模型需要將證券的期望收益率、期望的標準差和證券之間的期望相關係數作為已知數據作為基本輸入。如果這些數據 沒有估計誤差,馬考威茨模型就能夠保證得到有效的證券組合。但由於期望數據是未知的,需要進行統計估計,因此這些數據就不會沒有誤差。這種由於統計估計而帶來的數據輸入方面的不准確性會使一些資產類別的投資比例過高而使另一些資產類別的投資比例過低。
3.解的不穩定性。馬考威茨模型的另一個應用問題是輸人數據的微小改變會導致資產權重的很大變化。解的不穩定性限制了馬考威茨模型在實際制定資產配置政策方面的應用。如果基於季度對輸人數據進行重新估計,用馬考威茨模型就會得到新的資產權重的解,新的資產權重與上一季度的權重差異可能很大。這意味著必須對資產組合進行較大的調整,而頻繁的調整會使人們對馬考威茨模型產生不信任感。
4.重新配置的高成本。資產比例的調整會造成不必要的交易成本的上升。資產比例的調整會帶來很多不利的影響,因此正確的政策可能是維持現狀而不是最優化。
今天,在我國股票市場運用投資組合理論進行決策分析至少具有兩個方面的意義:
一是馬科維茨投資組合理論的核心思想是利用不同證券收益的相關性分散風險。
我國股票市場的投資者(包括機構投資者)在投資決策中主要應用技術分析面和基本面進行分析,而這兩種分析方法都是註重單隻證券,基本上忽略了證券收益的相關性;
二是在我國股票市場中,馬科維茨投資組合理論可以用來穩定地戰勝市場。
通過研究發現,市場綜合指數較大幅度地偏離了投資組合有效邊界。在此條件下,利用投資組合有效邊界完全可以穩定地戰勝市場。
本条目由以下用户参与贡献
Angle Roh,Vulture,村姑,山林,funwmy,Oval,Lolo,Zfj3000,Cabbage,Dan,Yixi,鲈鱼,Sicher,HEHE林,Tiffany,泡芙小姐,KAER,连晓雾,y桑,Gaoshan2013,Mis铭,林巧玲,Tracy,贾丹丹,Lin,FreeSoul,黄jw,苏青荇,134****8777,LuyinT,M id a04caf69a2226559ac5a782f43f35458.評論(共28條)
what does A and B means in the graph for optimal portfolio? please
都是超的 而且 沒有文獻連接
添加了部分參考文獻,希望對你有幫助~
對啊,沒有數學推導,我就是衝著這個來的
添加了新內容,希望對您有幫助!
MVP是minimum variance portfolio
應該是Minimum Variance Point








怎麼沒有圖?