鞅定價方法
出自 MBA智库百科(https://wiki.mbalib.com/)
鞅定價方法(Martingale Pricing Technique/martingale pricing theory/theory of martingale pricing)
目錄 |
Harrison 及 Kreos (1979)提出了一種求解金融衍生產品的定價方法——鞅定價方法。在鞅定價方法下,證券的價格可由折現該產品未來現金流量得到,且期望值折現在風險中立下計算。鞅定價方法比隨機微分方程簡單,也不會涉及複雜的積分。許多隨機微分方程不能求解的問題,鞅定價方法可輕易求解。
股票價格的隨機過程可以表示為:

WP 表示在概率測度P下的布朗運動。上述公式可以轉化為風險中性概率測度Q下的隨機過程:
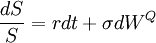
其中: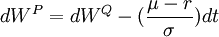 。
。
比較上述兩個公式可以發現,原來的μ已經被無風險利率r 取代,波動率σ 並未受到影響。
在風險中性概率測度Q下,股票價格的動態過程變為:
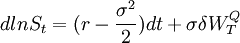
因此,相應的其動態過程可表示為:

在定價股票期權時,須計算EQ[ST | ST > K] ,它表示在到期日T,股價S_T大於執行價格K 的期望。
利用Girsanov 定理,經過一系列推導,可以得到:
EQ[ST | ST > K] = SErTN(d1)
計算出EQ[ST | ST > K] 後,然後再依據買、賣權以及其它相應的條件比較容易的得到股票期權的價格。
鞅這個術語早在20 世紀30 年代首先由Ville(1939)引進,但是基本概念來自於法國概率學家列維(Levy,1934)。但是真正把鞅理論發揚光大的則是美國數學家多布(Doob),他於1953 年的名著《隨機過程》一書中介紹了(包括上鞅分解問題在內的)他對於鞅論的系統研究成果。它引起了一般過程理論的研究,從此鞅成為現代概率和隨機過程的基礎,而且在決策和控制模型等方面有著重要應用,並得到快速發展。
鞅在20 世紀70 年代末期被引入金融經濟學用來描述資產的價格運動過程,最早出現在Pliska&Kreps。由於較多地藉助測度論,鞅顯得更加抽象,但是令人驚奇的是,它的引入不僅使得微觀金融理論分析(例如期權定價)變得更加簡潔和優雅;並且由於可以藉助現代數值計算技術,它還提供了更為強大的運算能力,而這對於實際工作又是至關重要的。
“鞅”一詞來源於法文martingale 的意譯,原意是指馬的籠套或者船的索具,同時也指一種逢輸就加倍賭註,直到贏為止的惡性賭博方法(double strategy)。但這都沒有說明它在金融學中的確切含義。鞅究竟是什麼呢?簡單的說,鞅是“公平”賭博(fair game)的數學模型。那麼什麼又是公平的賭博呢?假設一個人在參加賭博,他已經賭了n 次,正準備參加第n +1 次賭博。如果不做什麼手腳,他的運氣應當是同他以前的賭博經歷無關的,用Xn表示他在賭完第n次後擁有的賭本數,如果對於任何n都有
E(Xn | Xn − 1) = Xn − 1
成立,即賭博的期望收穫為0,僅能維持原有財富水平不變,就可以認為這種賭博在統計上是公平的。
在金融分析中,投資者通常會根據過去發生的事件來指導未來的投資決策,我們可以把X 設想為對由於信息發佈而產生波動的金融資產價格(過程),而EXn就是對這種價格運動的預測,而恰好鞅就是用條件數學期望來定義的,這種相似性就激發了使用鞅和與之相關的數學概念來描述金融資產價格運動過程特征的熱情,鞅在20 世紀80 年代以後迅速成為主流金融經濟學研究中標準的時髦。
案例一:鞅方法在期權定價中的應用[1]
期權是以期貨為基礎產生的一種金融工具,其本質是要求權利和義務分別進行定價。因此,購買方在支付一定的費用後將獲得在允許的時間內買或賣一定數量商品的選擇權。其中,期權的價格又是隨市場的供求變化而變化的,它的高低也直接影響到買賣雙發的盈虧,是交易的核心問題。
- 一、期權價格模型的發展
因此要求買賣雙方:(1)確保同時精確地觀察到期權的價格;(2)詳細考慮投資者是否已經利用了觀察到的套現機會;(3)考慮到交易所需要的費用;(4)全面估計在有效期內應支付的紅利。但在現實實踐中,以上四點非常難完成,甚至不可能完成。早在1900年法國金融學家Bachelier在其博士論文中首次提出了期權的布朗運動定價理論;1969年Sanuelson與Merton提出了以期權價格做為基礎資產價格函數的觀點,隨著B-S公式的問世,大大刺激了學者對期權的定價機制、方法、進行研究。
- 二、鞅方法的應用
鞅作為特殊的隨機過程滿足如下的條件:根據過程在s時刻之前的變化規律,其在將來某一時刻t的期望值等於過程在該時刻s的值。如在公平賭博過程中,用Z(t)表示某一賭徒在t時刻所擁有的本金,那麼Z=|Z(t),t>0|為鞅,也就是說無論該賭徒在s時刻以後的賭博中如何利用經驗,他在將來t時刻期望擁有的本金只能是Z(s)。
- 1.等價鞅測度的應用
等價鞅測度最基本的應用在於即期市場和期貨市場中的定價。目前國內的研究主要是把等價鞅測度應用於可轉換債券定價、資產組合最優定價和外匯市場定價等幾個方面。
在使用鞅方法時,首先要找到一個等同於P的概率測度P * ,然後通過公式(1)來貼現價格過程S * ,遵循P * 鞅分佈。
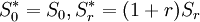 (1)
(1)
r:為隱含參數,僅與P有關。
如期權價格的計算,期權價格一般包括二個部分:無風險的和有風險的。其中風險價格滿足方程:
dst = st[μ(t)dt + σ(t)dbt] (2)
μ(t),σ(t)分別為瞬時期望收益率和波動率,{B_t,0\le t\le T}是定影在上的標準布朗運動,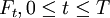 為產生的σ − 域。
為產生的σ − 域。
設 ,同時定義概率測度P * ,則可得:
,同時定義概率測度P * ,則可得:
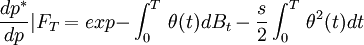 (3)
(3)
又如在計算美式買權價格的上下界時,首先假定T為到期時間,K為執行價格,t時刻買權的價格為:
![u(\tau,S_1)=sup E_{p^*}[e^{-\int_{\tau}^{t}\, r(s)ds}(S_r-K)^{+}]](/w/images/math/3/9/1/391a8f0b51c492e1cf348598911a6266.png) (4)
(4)
其中τ為[t,T]上的所有停時。設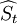 為P * 鞅,則可以證明:
為P * 鞅,則可以證明:
![e^{\int_{r}^{0}\, \rho(s)ds}c(t,S_t)\ge E_{p^*}[(S_r-K)^{+}e^{-\int_{\tau}^{t}\, r(s)ds}]](/w/images/math/2/9/f/29fe2adaa0a0781e0ca7bb238110a7fb.png) (5)
(5)
- 2.其他鞅方法的應用
在期權定價中鞅的應用還有指數半鞅的期權定價方法、對偶鞅測度的期權定價方法、連續鞅期權定價方法等等。
在期權定價中,鞅測度的引入對於掌握定價方法、優化組合、降低風險都是非常重要的,首先將期權定價的明確評估簡單化;其次,利用原期貨的相關價格行為給定了定價模型的無套利性質。使期貨價格過程的公平博弈性得以模型化。
- ↑ 呂潔.鞅方法在期權定價中的應用[J].財經界(學術),2010,(16):37
評論(共10條)
依然看不懂,鞅到底是什麼?能否用通俗的話給解釋一下
鞅就是期望值不變或為零的隨機過程
依然看不懂,鞅到底是什麼?能否用通俗的話給解釋一下
意思就是根據以前信息計算出來的現在預期收益等於之前的收益。
看不懂,有木有例子呀!
添加了新的案例,希望對您有幫哦~
依然看不懂,鞅到底是什麼?能否用通俗的話給解釋一下
很簡單的. Let (F_t) be a filtration on a probability space (Omega, F, P) where t>=0.
Let X_t be a family of integrable random variables. Suppose that (X_t) is adapted to the filtration (F_t), i.e. For each t, X_t is F_t/Borel(R)-measurable and for any 0<=s<t, E(X_t | F_s) =X_s,
then (X_t, F_t) is called a martingale.
E(Xn | Xn − 1) = Xn − 1 中間的"|"是什麼意思
條件概率的意思,意思在Xn-1已經發生的前提下
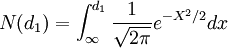 標準
標準







依然看不懂,鞅到底是什麼?能否用通俗的話給解釋一下