累積概率

出自 MBA智库百科(https://wiki.mbalib.com/)

累積概率（Cumulative probability）

　　累積概率是指在不確定分析中，當凈現值期望值相對較低，需進一步瞭解項目經濟效益發生在某一區間的可能性有多大，則應計算這個區間內所有可能取值的概率之和，即累積概率，用P(NPV≥0)表示。

　　自Hazen 於1914 年首次提出累積概率公式以來, 統計學者已導出幾十種經驗累積概率公式,其中大部分可用下列通式表達

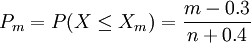　　 (1)

　　式中搖Pm--大於或等於Xm 的累積頻率; X--表示樣品; m--樣本從小到大的序號; n--樣品個數。為了能夠更加清楚地顯示數據性質, 必須對累積概率值進行坐標變換, 如正態變換、Gamma 變換、Logistic 變換等。

　　將變換後的坐標點{xm , φ(Pm )} (φ(Pm )(表示對Pm 進行變換) 投影在概率圖上, 就得到 概率累積曲線(圖1)。

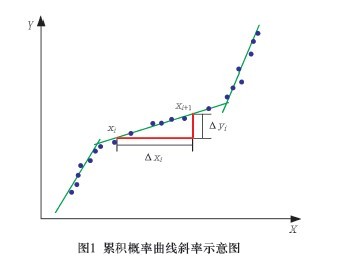
　　累積概率曲線上相鄰兩點間的斜率

　　Ki = ΔYi / ΔXi (2)

　　式中搖Ki--(Xi ,Xi+1 ) 兩點間的斜率;ΔYi--斜率縱向分量;ΔXi--斜率橫向分量;當數據個數確定之後,對於累積概率曲線上相鄰兩點來說,駐Yi 是一個常量,因此(Xi ,Xi+1 ) 之間的斜率只與ΔXi 有關。ΔXi 越小,斜率越大,曲線越陡。