風險中性
出自 MBA智库百科(https://wiki.mbalib.com/)
風險中性(Risk neutral)
目錄 |
風險中性是指在無風險條件下持有一筆貨幣財富的效用等於在風險條件下持有一筆貨幣財富的效用。其中兩種效用的對比需要考慮兩個變數:
1、期望效用(參照馮·諾曼-摩根斯頓效用函數);
2、期望值的效用
風險中性是相對於風險偏好和風險厭惡的概念,風險中性的投資者對自己承擔的風險並不要求風險補償.我們把每個人都是風險中性的世界稱之為風險中性世界 (Risk-Neutral World),這樣的世界里,投資者對風險不要補償,所有證券的預期收益率都是無風險利率.需要強調的是,風險中性假設下得到的衍生物估值同樣可以應用於非風險中性的世界.真實世界里的投資者儘管在風險偏好方面存在差異,但當套利機會出現時,投資者無論風險偏好如何都會採取套利行為,消除套利機會後的均衡價格與投資者的風險偏好無關,羅斯(Ross,1976)嚴格證明瞭這一邏輯.
風險中性者並不介意一項投機是否具有比較確定或者不那麼確定的結果。他們只是根據預期的貨幣價值來選擇投機,特別而言,他們要使期望貨幣價值最大化。
風險中性實例分析[1]
1.期望效用
在分析風險下的消費者行為時,期望效用和期望值的效用是兩個經常要用到的概念。用彩票的例子來說明期望效用的概念。假定某消費者所面臨的一種彩票具有兩種可能的結果。當第一種結果發生時,該消費者擁有的貨幣財富量為W1.當第二種結果發生是,該消費者擁有的貨幣財富量為W2。第一種結果和第二種結果發生的概率分別為P和(1-P),其中0≤P≤1。假設消費者在擁有的貨幣財富量為W1和W2所能獲取的收入效用分別為U(W1)和U(W2),那麼彩票的期望效用函數為
![E[U(W_1,W_2)]=P\cdots U(W_1)+(1-P)\cdots U(W_2)](/w/images/math/9/7/a/97a08415b8605fb3acf8b4400f0106bc.png)
期望效用函數也被稱為馮·諾曼一摩根斯坦效用函數。由上式可知,消費者的期望效用就是消費者在風險條件下可能得到的各種結果的效用的加權平均數——效用的數學期望值。顯然,期望效用帶有基數效用的性質。由於期望效用函數的建立,對不確定條件下的消費者面臨風險的行為的分析,就轉變成為對消費者追求期望效用最大化行為的分析。在決策環境確定情況下,消費者追求效用最大化為建立決策分析的目標:在風險情況下,消費者追求期望效用最大化為建立決策分析的目標。
2.期望值的效用
期望值的效用與期望效用的含義不同,我們仍用上述彩票的例子來說明。一張彩票期望值為
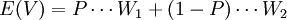
由上式可知,彩票的期望值是彩票不同結果下的消費者所擁有的貨幣財富量的加權平均數。相應地,彩票期望值的效用為
![U[E(V)]=U[P\cdots W_1+(1-P)\cdots W_2]](/w/images/math/7/a/f/7af414ca6152ca8d7ab014c71081c4af.png)
關於期望效用和期望值的效用的區別及其具體應用,將在以下對消費者的風險態度的分析中得到體現。
不同的行為者對風險的態度是存在差異的,一部分人可能喜歡刺激,另一部分人則可能更願意“求穩”。根據風險理論,行為者對風險的態度可以劃分為3類:風險迴避者、風險愛好者和風險中立者。這三類風險態度的判斷標準如下:假定消費者在無風險的情況下所能獲得確定性收入與他在有風險的情況下能夠獲得的期望收入值相等。如果消費者對於確定性收入的偏好大於有風險條件下期望收入的偏好,那麼該消費者是風險迴避者;如果消費者對於確定性收入的偏好小於有風險條件下期望收入的偏好,那麼該消費者是風險愛好者;如果消費者對於確定性收入的偏好等於有風險條件下期望收入的偏好,那麼該消費者是風險中立者。
下麵以上述消費者面臨一張彩票的情況為例,來分析消費者的風險態度。首先假定消費者在無風險條件下(即不購買彩票的條件下)可以持有的確定的貨幣財富量等於彩票的期望值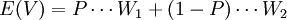 ,對比不同風險偏好者期望值的效用和期望效用。
,對比不同風險偏好者期望值的效用和期望效用。
在圖(a)中,在無風險持有確定的貨幣財富量條件下消費者期望值的效用U[E(V)]大於在風險條件下的期望效用研E[U(W1,W2)]。![U[E(V)=P\cdots W_1+(1-P)\cdots W_2]>E(V)=P\cdots U(W_1)+(1-P)\cdots U(W_2)](/w/images/math/1/3/5/135f100e0065645d51a8bba601c5a48b.png) ,則該消費者為風險迴避者。
,則該消費者為風險迴避者。
在圖(b)中,在無風險持有貨幣財富條件下,消費者財富期望值的效用U[E(V)]小於在風險條件下的期望效用E[U(W1,W2)]。![U[E(V)=P\cdots W_1+(1-P)\cdots W_2]<E(V)=P\cdots U(W_1)+(1-P)\cdots U(W_2)](/w/images/math/d/2/8/d28fbc6e079be621e04326d99314a7aa.png) ,則該消費者為風險愛好者。
,則該消費者為風險愛好者。
在圖(c)中,在無風險持有貨幣財富條件下,消費者財富期望值的效用U[E(V)]等於在風險條件下的期望效用研E(U(W_1,W_2))]。![U[E(V)=P\cdots W_1+(1-P)\cdots W_2]=E(V)=P\cdots U(W_1)+(1-P)\cdots U(W_2)](/w/images/math/3/8/6/38662b424239908663b98b3a06f03546.png) ,則該消費者為風險中立者。
,則該消費者為風險中立者。
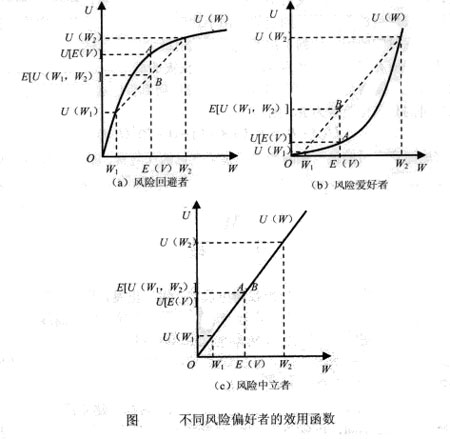
與以上的分析相對應,消費者的風險態度可以根據消費者效用函數的特征來判斷。假定消費者的效用函數為U=U(形)。其中,形為貨幣財富量,且效用函數U=U(w)為增函數。如圖(a)所示,風險迴避者的效用函數是嚴格凹的,效用曲線上任意兩點間的弧部高於兩點間的弦。圖中的4點是期望值的效用,它代表消費者在無風險條件下持有一筆確定的貨幣財富量的效用![U[P\cdots W_1+(1-P)\cdots W_2]](/w/images/math/c/3/2/c325ebf7eb928aec1afec87daffd17cf.png) ;圖中的B點代表擁有一張具有風險的彩票的期望效用
;圖中的B點代表擁有一張具有風險的彩票的期望效用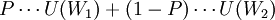 。顯然,A點高於B點。在圖(b)中,風險愛好者的效用函數是嚴格凸的,效用曲線上任意兩點間的弧部低於兩點間的弦,期望值的效用點A低於期望效用點B。在圖(c)中,風險中立者的效用函數是線性的,期望值的效用點A與期望效用點B重合。
。顯然,A點高於B點。在圖(b)中,風險愛好者的效用函數是嚴格凸的,效用曲線上任意兩點間的弧部低於兩點間的弦,期望值的效用點A低於期望效用點B。在圖(c)中,風險中立者的效用函數是線性的,期望值的效用點A與期望效用點B重合。
因此,可以通過消費者的效用曲線的嚴格凹、嚴格凸和線性的特征,判斷消費者的風險態度為風險迴避者、風險愛好者和風險中立者。也可以進一步用效用函數的二階導數表述以上曲線特征。當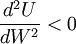 ,效用曲線嚴格凹的情況下,消費者為風險迴避者;當
,效用曲線嚴格凹的情況下,消費者為風險迴避者;當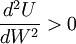 ,效用曲線嚴格凸的情況下,消費者為風險愛好者;當
,效用曲線嚴格凸的情況下,消費者為風險愛好者;當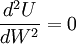 ,效用曲線線性的情況下,消費者為風險中立者。
,效用曲線線性的情況下,消費者為風險中立者。
- ↑ 畢軍賢.微觀經濟學[M].科學出版社,2007.9.
評論(共3條)
恕在下愚鈍..期望效用與期望值的效用有何區別?
添加了內容和案例,希望對您有幫助!
舉例來說,每個人的效用可以看做是財富的函數,你有五塊錢是一個效用,你有十塊錢又是一個效用,但是有十塊錢比有5塊錢的效用要高,現在有一種投資你需要投7.5塊,結果是有可能得到10塊,也有可能得到5塊,假設這種概率是各50%。那麼你期望投資結果獲得值是7.5,對應你的效用曲線,7.5塊給你帶來的效用是a,這是期望值得效用;而當你的投資獲得5塊時你會有一種效用,當你的投資結果是10的時候你又有一種效用,獲得這兩種效用的概率和你投資結果的概率相同,即各50%,這兩種效用的加權平均值假設是b,這就是期望效用。如果a等於b,你就是風險中性的,如果a大於b你就是風險厭惡的,如果a小於b你就是風險偏好的。








恕在下愚鈍..期望效用與期望值的效用有何區別?