风险中性
出自 MBA智库百科(https://wiki.mbalib.com/)
风险中性(Risk neutral)
目录 |
风险中性是指在无风险条件下持有一笔货币财富的效用等于在风险条件下持有一笔货币财富的效用。其中两种效用的对比需要考虑两个变量:
1、期望效用(参照冯·诺曼-摩根斯顿效用函数);
2、期望值的效用
风险中性是相对于风险偏好和风险厌恶的概念,风险中性的投资者对自己承担的风险并不要求风险补偿.我们把每个人都是风险中性的世界称之为风险中性世界 (Risk-Neutral World),这样的世界里,投资者对风险不要补偿,所有证券的预期收益率都是无风险利率.需要强调的是,风险中性假设下得到的衍生物估值同样可以应用于非风险中性的世界.真实世界里的投资者尽管在风险偏好方面存在差异,但当套利机会出现时,投资者无论风险偏好如何都会采取套利行为,消除套利机会后的均衡价格与投资者的风险偏好无关,罗斯(Ross,1976)严格证明了这一逻辑.
风险中性者并不介意一项投机是否具有比较确定或者不那么确定的结果。他们只是根据预期的货币价值来选择投机,特别而言,他们要使期望货币价值最大化。
风险中性实例分析[1]
1.期望效用
在分析风险下的消费者行为时,期望效用和期望值的效用是两个经常要用到的概念。用彩票的例子来说明期望效用的概念。假定某消费者所面临的一种彩票具有两种可能的结果。当第一种结果发生时,该消费者拥有的货币财富量为W1.当第二种结果发生是,该消费者拥有的货币财富量为W2。第一种结果和第二种结果发生的概率分别为P和(1-P),其中0≤P≤1。假设消费者在拥有的货币财富量为W1和W2所能获取的收入效用分别为U(W1)和U(W2),那么彩票的期望效用函数为
![E[U(W_1,W_2)]=P\cdots U(W_1)+(1-P)\cdots U(W_2)](/w/images/math/9/7/a/97a08415b8605fb3acf8b4400f0106bc.png)
期望效用函数也被称为冯·诺曼一摩根斯坦效用函数。由上式可知,消费者的期望效用就是消费者在风险条件下可能得到的各种结果的效用的加权平均数——效用的数学期望值。显然,期望效用带有基数效用的性质。由于期望效用函数的建立,对不确定条件下的消费者面临风险的行为的分析,就转变成为对消费者追求期望效用最大化行为的分析。在决策环境确定情况下,消费者追求效用最大化为建立决策分析的目标:在风险情况下,消费者追求期望效用最大化为建立决策分析的目标。
2.期望值的效用
期望值的效用与期望效用的含义不同,我们仍用上述彩票的例子来说明。一张彩票期望值为
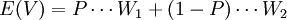
由上式可知,彩票的期望值是彩票不同结果下的消费者所拥有的货币财富量的加权平均数。相应地,彩票期望值的效用为
![U[E(V)]=U[P\cdots W_1+(1-P)\cdots W_2]](/w/images/math/7/a/f/7af414ca6152ca8d7ab014c71081c4af.png)
关于期望效用和期望值的效用的区别及其具体应用,将在以下对消费者的风险态度的分析中得到体现。
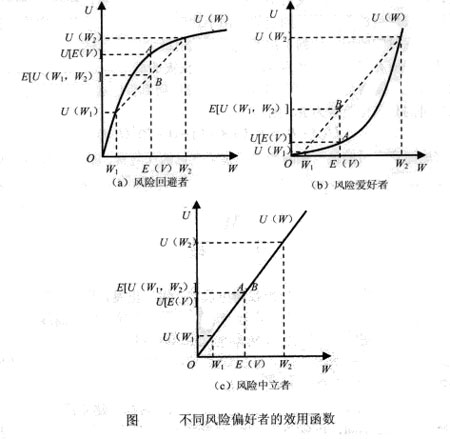
不同的行为者对风险的态度是存在差异的,一部分人可能喜欢刺激,另一部分人则可能更愿意“求稳”。根据风险理论,行为者对风险的态度可以划分为3类:风险回避者、风险爱好者和风险中立者。这三类风险态度的判断标准如下:假定消费者在无风险的情况下所能获得确定性收入与他在有风险的情况下能够获得的期望收入值相等。如果消费者对于确定性收入的偏好大于有风险条件下期望收入的偏好,那么该消费者是风险回避者;如果消费者对于确定性收入的偏好小于有风险条件下期望收入的偏好,那么该消费者是风险爱好者;如果消费者对于确定性收入的偏好等于有风险条件下期望收入的偏好,那么该消费者是风险中立者。
下面以上述消费者面临一张彩票的情况为例,来分析消费者的风险态度。首先假定消费者在无风险条件下(即不购买彩票的条件下)可以持有的确定的货币财富量等于彩票的期望值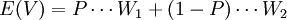 ,对比不同风险偏好者期望值的效用和期望效用。
,对比不同风险偏好者期望值的效用和期望效用。
在图(a)中,在无风险持有确定的货币财富量条件下消费者期望值的效用U[E(V)]大于在风险条件下的期望效用研E[U(W1,W2)]。![U[E(V)=P\cdots W_1+(1-P)\cdots W_2]>E(V)=P\cdots U(W_1)+(1-P)\cdots U(W_2)](/w/images/math/1/3/5/135f100e0065645d51a8bba601c5a48b.png) ,则该消费者为风险回避者。
,则该消费者为风险回避者。
在图(b)中,在无风险持有货币财富条件下,消费者财富期望值的效用U[E(V)]小于在风险条件下的期望效用E[U(W1,W2)]。![U[E(V)=P\cdots W_1+(1-P)\cdots W_2]<E(V)=P\cdots U(W_1)+(1-P)\cdots U(W_2)](/w/images/math/d/2/8/d28fbc6e079be621e04326d99314a7aa.png) ,则该消费者为风险爱好者。
,则该消费者为风险爱好者。
在图(c)中,在无风险持有货币财富条件下,消费者财富期望值的效用U[E(V)]等于在风险条件下的期望效用研E(U(W_1,W_2))]。![U[E(V)=P\cdots W_1+(1-P)\cdots W_2]=E(V)=P\cdots U(W_1)+(1-P)\cdots U(W_2)](/w/images/math/3/8/6/38662b424239908663b98b3a06f03546.png) ,则该消费者为风险中立者。
,则该消费者为风险中立者。
与以上的分析相对应,消费者的风险态度可以根据消费者效用函数的特征来判断。假定消费者的效用函数为U=U(形)。其中,形为货币财富量,且效用函数U=U(w)为增函数。如图(a)所示,风险回避者的效用函数是严格凹的,效用曲线上任意两点间的弧部高于两点间的弦。图中的4点是期望值的效用,它代表消费者在无风险条件下持有一笔确定的货币财富量的效用![U[P\cdots W_1+(1-P)\cdots W_2]](/w/images/math/c/3/2/c325ebf7eb928aec1afec87daffd17cf.png) ;图中的B点代表拥有一张具有风险的彩票的期望效用
;图中的B点代表拥有一张具有风险的彩票的期望效用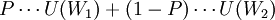 。显然,A点高于B点。在图(b)中,风险爱好者的效用函数是严格凸的,效用曲线上任意两点间的弧部低于两点间的弦,期望值的效用点A低于期望效用点B。在图(c)中,风险中立者的效用函数是线性的,期望值的效用点A与期望效用点B重合。
。显然,A点高于B点。在图(b)中,风险爱好者的效用函数是严格凸的,效用曲线上任意两点间的弧部低于两点间的弦,期望值的效用点A低于期望效用点B。在图(c)中,风险中立者的效用函数是线性的,期望值的效用点A与期望效用点B重合。
因此,可以通过消费者的效用曲线的严格凹、严格凸和线性的特征,判断消费者的风险态度为风险回避者、风险爱好者和风险中立者。也可以进一步用效用函数的二阶导数表述以上曲线特征。当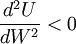 ,效用曲线严格凹的情况下,消费者为风险回避者;当
,效用曲线严格凹的情况下,消费者为风险回避者;当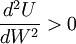 ,效用曲线严格凸的情况下,消费者为风险爱好者;当
,效用曲线严格凸的情况下,消费者为风险爱好者;当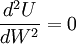 ,效用曲线线性的情况下,消费者为风险中立者。
,效用曲线线性的情况下,消费者为风险中立者。
- ↑ 毕军贤.微观经济学[M].科学出版社,2007.9.
评论(共3条)
恕在下愚钝..期望效用与期望值的效用有何区别?
添加了内容和案例,希望对您有帮助!
举例来说,每个人的效用可以看做是财富的函数,你有五块钱是一个效用,你有十块钱又是一个效用,但是有十块钱比有5块钱的效用要高,现在有一种投资你需要投7.5块,结果是有可能得到10块,也有可能得到5块,假设这种概率是各50%。那么你期望投资结果获得值是7.5,对应你的效用曲线,7.5块给你带来的效用是a,这是期望值得效用;而当你的投资获得5块时你会有一种效用,当你的投资结果是10的时候你又有一种效用,获得这两种效用的概率和你投资结果的概率相同,即各50%,这两种效用的加权平均值假设是b,这就是期望效用。如果a等于b,你就是风险中性的,如果a大于b你就是风险厌恶的,如果a小于b你就是风险偏好的。








恕在下愚钝..期望效用与期望值的效用有何区别?