Black-Scholes期權定價模型
出自 MBA智库百科(https://wiki.mbalib.com/)
Black-Scholes期權定價模型(Black-Scholes Option Pricing Model),布萊克-肖爾斯期權定價模型
目錄 |
1997年10月10日,第二十九屆諾貝爾經濟學獎授予了兩位美國學者,哈佛商學院教授羅伯特·默頓(RoBert Merton)和斯坦福大學教授邁倫·斯克爾斯(Myron Scholes)。他們創立和發展的布萊克——斯克爾斯期權定價模型(Black Scholes Option Pricing Model)為包括股票、債券、貨幣、商品在內的新興衍生金融市場的各種以市價價格變動定價的衍生金融工具的合理定價奠定了基礎。
斯克爾斯與他的同事、已故數學家費雪·布萊克(Fischer Black)在70年代初合作研究出了一個期權定價的複雜公式。與此同時,默頓也發現了同樣的公式及許多其它有關期權的有用結論。結果,兩篇論文幾乎同時在不同刊物上發表。所以,布萊克—斯克爾斯定價模型亦可稱為布萊克—斯克爾斯—默頓定價模型。默頓擴展了原模型的內涵,使之同樣運用於許多其它形式的金融交易。瑞典皇家科學協會(The Royal Swedish Academyof Sciencese)贊譽他們在期權定價方面的研究成果是今後25年經濟科學中的最傑出貢獻。
1、股票價格行為服從對數正態分佈模式;
2、在期權有效期內,無風險利率和金融資產收益變數是恆定的;
3、市場無摩擦,即不存在稅收和交易成本,所有證券完全可分割;
4、金融資產在期權有效期內無紅利及其它所得(該假設後被放棄);
5、該期權是歐式期權,即在期權到期前不可實施。
6、不存在無風險套利機會;
7、證券交易是持續的;
8、投資者能夠以無風險利率借貸。
(二)榮獲諾貝爾經濟學獎的B-S定價公式[1]
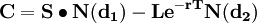
其中:
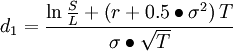
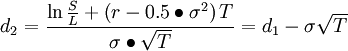
第一,該模型中無風險利率必須是連續複利形式。一個簡單
的或不連續的無風險利率(設為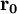 )一般是一年複利
一次,而r要求利率連續複利。
)一般是一年複利
一次,而r要求利率連續複利。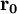 必須轉化為r方能
代入上式計算。兩者換算關係為:
必須轉化為r方能
代入上式計算。兩者換算關係為: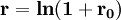 或
或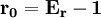 。例如
。例如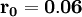 ,
則r=ln(1+0.06)=0.0583,即100以5.83%的連續複利投資第二年將獲106,
該結果與直接用
,
則r=ln(1+0.06)=0.0583,即100以5.83%的連續複利投資第二年將獲106,
該結果與直接用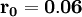 計算的答案一致。
計算的答案一致。
第二,期權有效期T的相對數表示,即期權有效天數與一年365
天的比值。如果期權有效期為100天,則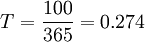 。
。
B-S定價模型的推導與運用[1]
(一)B-S模型的推導B-S模型的推導是由看漲期權入手的,對於一項看漲期權,其到期的期值是:
![\mathbf{E[G]=E[max(S_t-L,0)]}](/w/images/math/f/1/4/f14e1c9a6ccabbf3ed91f1ef4b2cd071.png)
其中,
- E[G]—看漲期權到期期望值
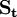 —到期所交易金融資產的市場價值
—到期所交易金融資產的市場價值
- L—期權交割(實施)價
到期有兩種可能情況:
1、如果St > L,則期權實施以進帳(In-the-money)生效,且max(St − L,O) = St − L
2、如果St < L,則期權所有人放棄購買權力,期權以出帳(Out-of-the-money)失效,且有:
max(St − L,O) = 0
從而:
![E[C_t]=P\times E[S_t|S_t>L]+(1-P)\times O=P\times E[S_t|S_t>L]-L)](/w/images/math/3/7/a/37a16f68ba5880daf3099875cb81b85d.png)
其中:P:(St > L)的概率E[St | St > L]:既定(St > L)下St的期望值將E[G]按有效期無風險連續複利rT貼現,得期權初始合理價格:
C = Pe − rT(E[St | St > L] − L)這樣期權定價轉化為確定P和E[St | St > L]。
首先,對收益進行定義。與利率一致,收益為金融資產期權交割日市場價格(St)與現價(S)比值的對數值,即收益 = lnSt / S = ln(St / L)。由假設1收益服從對數正態分佈,即ln(St / L)~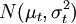 ,所以E[lN(St / S] = μt,St / S~
,所以E[lN(St / S] = μt,St / S~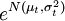 可以證明,相對價格期望值大於eμt,為:E[St / S] = eμt + σ2T2 = erT從而,μt = T(r − σ2),且有σt = σT
可以證明,相對價格期望值大於eμt,為:E[St / S] = eμt + σ2T2 = erT從而,μt = T(r − σ2),且有σt = σT
其次,求(St > L)的概率P,也即求收益大於(LS)的概率。已知正態分佈有性質:Pr06[ξ > x] = 1 − N(x − μσ)其中:
ζ:正態分佈隨機變數
x:關鍵值
μ-ζ的期望值
σ-ζ的標準差
所以:P = Pr06[St > 1] = Pr06[lnSt / s] > lnLS = :LN − lnLS − (r − σ2)TσTnc4 由對稱性:1 − N(d) = N( − d)P = NlnSL + (r − σ2)TσTarS。
第三,求既定St > L下St的期望值。因為E[St | St > L]處於正態分佈的L到∞範圍,所以,
E[St | St] > = SerTN(d1)N(d2)
其中: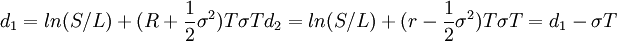
最後,將P、E[St | St] > L]代入(C = Pe − rT(E[St | St > L] − L))式整理得B-S定價模型:C = SN(d1) − Le − rTN(d2)
(二)看跌期權定價公式的推導
B-S模型是看漲期權的定價公式,根據售出—購進平價理論(Put-callparity)可以推導出有效期權的定價模型,由售出—購進平價理論,購買某股票和該股票看跌期權的組合與購買該股票同等條件下的看漲期權和以期權交割價為面值的無風險折扣發行債券具有同等價值,以公式表示為:
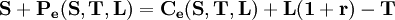
移項得:
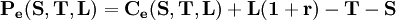 ,
,
將B-S模型代入整理得:
![\mathbf{P=Le^{-rT}\left[1-N(d_2)\right]-S\left[1-N(d_1)\right]}](/w/images/math/3/3/1/331a1c311a240041f46498273f0df6a9.png)
此即為看跌期權初始價格定價模型。
(三)B-S模型應用實例
假設市場上某股票現價S為 164,無風險連續複利利率γ是0.0521,市場方差σ2為0.0841,那麼實施價格L是165,有效期T為0.0959的期權初始合理價格計算步驟如下:
①求d1:
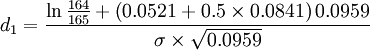 =0.0328
=0.0328
②求d2:
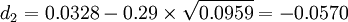
③查標準正態分佈函數表,得:N(0.03)=0.5120 N(-0.06)=0.4761
④求C:
C=164×0.5120-165×e-0.0521×0.0959×0.4761=5.803
因此理論上該期權的合理價格是5.803。如果該期權市場實際價格是5.75,那麼這意味著該期權有所低估。在沒有交易成本的條件下,購買該看漲期權有利可圖。
B-S模型只解決了不分紅股票的期權定價問題,默頓發展了B-S模型,使其亦運用於支付紅利的股票期權。
(一)存在已知的不連續紅利假設某股票在期權有效期內某時間t(即除息日)支付已知紅利Dt,只需將該紅利現值從股票現價S中除去,將調整後的股票價值S′代入B-S模型中即可:S' = S − Dte − rT。如果在有效期記憶體在其它所得,依該法一一減去。從而將B-S模型變型得新公式:

(二)存在連續紅利支付是指某股票以一已知分紅率(設為δ)支付不間斷連續紅利,假如某公司股票年分紅率δ為0.04,該股票現值為164,從而該年可望得紅利164×004= 6.56。值得註意的是,該紅利並非分4季支付每季164;事實上,它是隨美元的極小單位連續不斷的再投資而自然增長的,一年累積成為6.56。因為股價在全年是不斷波動的,實際紅利也是變化的,但分紅率是固定的。因此,該模型並不要求紅利已知或固定,它只要求紅利按股票價格的支付比例固定。
在此紅利現值為:S(1-E-δT),所以S′=S•E-δT,以S′代S,得存在連續紅利支付的期權定價公式:C=S•E-δT•N(D1)-L•E-γT•N(D2)
自B-S模型1973年首次在政治經濟雜誌(Journal of Political Economy)發表之後,芝加哥期權交易所的交易商們馬上意識到它的重要性,很快將B-S模型程式化輸入電腦應用於剛剛營業的芝加哥期權交易所。該公式的應用隨著電腦、通訊技術的進步而擴展。到今天,該模型以及它的一些變形已被期權交易商、投資銀行、金融管理者、保險人等廣泛使用。衍生工具的擴展使國際金融市場更富有效率,但也促使全球市場更加易變。新的技術和新的金融工具的創造加強了市場與市場參與者的相互依賴,不僅限於一國之內還涉及他國甚至多國。結果是一個市場或一個國家的波動或金融危機極有可能迅速的傳導到其它國家乃至整個世界經濟之中。我國金融體制不健全、資本市場不完善,但是隨著改革的深入和向國際化靠攏,資本市場將不斷發展,匯兌制度日漸完善,企業也將擁有更多的自主權從而面臨更大的風險。因此,對規避風險的金融衍生市場的培育是必需的,對衍生市場進行探索也是必要的,我們才剛剛起步。
B-S模型問世以來,受到普遍的關註與好評,有的學者還對其準確性開展了深入的檢驗。但同時,不少經濟學家對模型中存在的問題亦發表了不同的看法,並從完善與發展B-S模型的角度出發,對之進行了擴展。
1977年美國學者伽萊(galai)利用芝加哥期權交易所上市的股票權的數據,首次對布-肖模型進行了檢驗。此後,不少學者在這一領域內作了有益的探索。其中比較有影響的代表人物有特裡皮(trippi)、奇拉斯(chiras)、曼納斯特(manuster)、麥克貝斯(macbeth)及默維勒(merville)等。綜合起來,這些檢驗得到瞭如下一些具有普遍性的看法:
1.模型對平值期權的估價令人滿意,特別是對剩餘有效期限超過兩月,且不支付紅利者效果尤佳。
2.對於高度增值或減值的期權,模型的估價有較大偏差,會高估減值期權而低估增值期權。
3.對臨近到期日的期權的估價存在較大誤差。
4.離散度過高或過低的情況下,會低估低離散度的買入期權,高估高離散度的買方期權。但總體而言,布-肖模型仍是相當準確的,是具有較強實用價值的定價模型。
對布-肖模型的檢驗著眼於從實際統計數據進行分析,對其表現進行評估。而另外的一些研究則從理論分析入手,提出了布-肖模型存在的問題,這集中體現於對模型假設前提合理性的討論上。不少學者認為,該模型的假設前提過嚴,影響了其可靠性,具體表現在以下幾方面:
首先,對股價分佈的假設。布-肖模型的一個核心假設就是股票價格波動滿足幾何維納過程,從而股價的分佈是對數正態分佈,這意味著股價是連續的。麥頓(merton)、約翰·考克斯(John Carrington Cox)、斯蒂芬·羅斯(Stephen A. Ross)、馬克·魯賓斯坦(Mark Rubinstein)等人指出,股價的變動不僅包括對數正態分佈的情況,也包括由於重大事件而引起的跳起情形,忽略後一種情況是不全面的。他們用二項分佈取代對數正態分佈,構建了相應的期權定價模型。
其次,關於連續交易的假設。從理論上講,投資者可以連續地調整期權與股票間的頭寸狀況,得到一個無風險的資產組合。但實踐中這種調整必然受多方面因素的制約:1.投資者往往難以按同一的無風險利率借入或貸出資金;2.股票的可分性受具體情況制約;3.頻繁的調整必然會增加交易成本。因此,現實中常出現非連續交易的情況,此時,投資者的風險偏好必然影響到期權的價格,而布-肖模型並未考慮到這一點。
再次,假定股票價格的離散度不變也與實際情況不符。布萊克本人後來的研究表明,隨著股票價格的上升,其方差一般會下降,而並非獨立於股價水平。有的學者(包括布萊克本人)曾想擴展佈-肖模型以解決變動的離散度的問題,但至今未取得滿意的進展。
此外,不考慮交易成本及保證金等的存在,也與現實不符。而假設期權的基礎股票不派發股息更限制了模型的廣泛運用。不少學者認為,股息派發的時間與數額均會對期權價格產生實質性的影響,不能不加以考察。他們中有的人對模型進行適當調整,使之能反映股息的影響。具體來說,如果是歐洲買方期權,調整的方法是將股票價格減去股息(d)的現值替代原先的股價,而其他輸入變數不變,代入布-肖模型即可。若是美國買方期權,情況稍微複雜。第一步先按上面的辦法調整後得到不提早執行情況下的價格。第二步需估計在除息日前立即執行情況下期權的價格,將調整後的股價替代實際股價,距除息日的時間替代有效期限、股息調整後的執行價格(x-d)替代實際執行價格,連同無風險利率與股價離散度等變數代入模型即可。第三步選取上述兩種情況下期權的較大值作為期權的均衡價格。需指出的是,當支付股息的情況比較複雜時,這種調整難度很大。
本条目由以下用户参与贡献
Angle Roh,山林,Wwdz,funwmy,Vulture,Zfj3000,Kane0135,Alphasunmoon,缺,Dan,Ykk1999,Cabbage,Jamessong,Xuhlj,Sherry,鲈鱼,泡芙小姐,Yixi,可恨密码记不住,林巧玲,楼康男,Chixg,不死鸟他爹,155****9255,M id 755cac01e754f10c73eaebef3fb59a4c.評論(共55條)
該條目內容是本人發的,因公式錯誤,而困擾了大家,本人深感抱歉,現已做了更改補充,不正確之處,請大家及時更改,謝謝! 個別公式看起來比較零亂,那是顯示的原因
您說的第四條假設後來被放棄了麽?不是還有根據第四條假設的變形公式麽?敬請回覆~ guoxiaolong369@163.com9
N(d1)是買權執行的概率嗎?
你的概率推導輸入上面有不少錯誤,比如括弧少打,指數,下標位置不對
謝謝指正,已對內容進行修改。MBA智庫是可以自由編輯的,您也可以參與完善。
"因此理論上該期權的合理價格是5.803。如果該期權市場實際價格是5.75,那麼這意味著該期權有所低估。在沒有交易成本的條件下,購買該看漲期權有利可圖。 "——————這句話不很荒謬嗎?難道經濟學家們和學人們看不出來?
荒謬荒謬荒謬!雖然不怎麼能看懂這公式,但從邏輯上看這種思路有很大問題,應該換種思路來思考計算。本人有種不同的分析計算思路,但限於時間,暫時先這樣記下。
期權的合理價格是5.803。如果該期權市場實際價格是5.75 直接就套利了
在BS的假設下,馬上就會有人破產
所以不僅僅是獲利這麼簡單
荒謬荒謬荒謬!雖然不怎麼能看懂這公式,但從邏輯上看這種思路有很大問題,應該換種思路來思考計算。本人有種不同的分析計算思路,但限於時間,暫時先這樣記下。
你把自己吹這麼厲害下個nobel你拿?
我覺得這個你strict price 你應該用 E來表示~!!!!這樣比較清楚,還有那個正太分佈的公式。。。初期模型不是那樣的。。那個應該是轉換後的吧?????
我覺得這個你strict price 你應該用 E來表示~!!!!這樣比較清楚,還有那個正太分佈的公式。。。初期模型不是那樣的。。那個應該是轉換後的吧?????
執行價格,又叫敲定價格,是strike price。。。。
看到某些人的評論,實在認為好笑。就像70年代那時的學術氣氛,總以為初等數學就是高峰了一樣。默頓的理論很深的。大家耐心研究吧。實際意義很大的,很多理念太令人振奮了。
荒謬荒謬荒謬!雖然不怎麼能看懂這公式,但從邏輯上看這種思路有很大問題,應該換種思路來思考計算。本人有種不同的分析計算思路,但限於時間,暫時先這樣記下。
不裝會不會死?請問您哪裡畢業,哪裡高就,有什麼證書?既然看都看不懂,好意思說人家荒謬?
假設6的意思你理解錯誤了。假設6是指no arbitrage。不是屏蔽利潤。從option中賺錢這不是arbitrage的一種體現。
執行價格,又叫敲定價格,是strike price。。。。
又叫exercise price...
又叫exercise price...
strike price是履約價,也就是約定的價格 exercise price 則是執行的價格,與履約價並不同:)
strike price是履約價,也就是約定的價格 exercise price 則是執行的價格,與履約價並不同:)
膜拜
E[C_t]=P\times E[S_t|S_t>L]+(1-P)\times O=P\times E[S_t|S_t>L]-L) 第一個是(Ct|St>L)
strike price是履約價,也就是約定的價格 exercise price 則是執行的價格,與履約價並不同:)
你履約的價格,不就是你執行的價格嗎…
"因此理論上該期權的合理價格是5.803。如果該期權市場實際價格是5.75,那麼這意味著該期權有所低估。在沒有交易成本的條件下,購買該看漲期權有利可圖。 "——————這句話不很荒謬嗎?難道經濟學家們和學人們看不出來?
一點也不,市場價格5.75,合理價格5.803,不考慮交易成本,用5.75購買5.803,沒看出哪裡有問題。
這裡的“有利可圖”是指贏的概率大於輸的概率。金融市場有不確定性,不能保證穩贏,但如果很多次參與贏面大的交易,最後結果肯定是“有利可圖”。
bs期權定價的檢驗方案
N(d1)是給我解釋下什麼意思。。。N(d2)看懂了,d1沒看懂。。。
d1,d2服從正態分佈
你把自己吹這麼厲害下個nobel你拿?
你沒GET到這句話的梗。參見費馬猜想。
荒謬荒謬荒謬!雖然不怎麼能看懂這公式,但從邏輯上看這種思路有很大問題,應該換種思路來思考計算。本人有種不同的分析計算思路,但限於時間,暫時先這樣記下。
什麼當代費馬
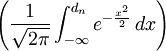 ,在此應當說明兩點:
,在此應當說明兩點:








公式怎麼感覺怪怪的啊……