連續複利
出自 MBA智库百科(https://wiki.mbalib.com/)
連續複利(Continuous compounding)
目錄 |
複利就是複合利息，它是指每年的收益還可以產生收益，具體是將整個借貸期限分割為若幹段，前一段按本金計算出的利息要加入到本金中，形成增大了的本金，作為下一段計算利息的本金基數，直到每一段的利息都計算出來，加總之後，就得出整個借貸期內的利息，簡單來說就是俗稱的利滾利。
而連續複利則是指在期數趨於無限大的極限情況下得到的利率，此時不同期之間的間隔很短，可以看作是無窮小量。
設本金為p0 ，年利率為i，當每年含有m個複利結算周期（若一個月為一個複利結算周期，則m=12，若以一季度為一個複利結算周期，則m=4）時，則n年後的本利和為：
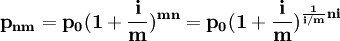
當複利結算的周期數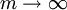
（這意味著資金運用率最大限度的提高）時，
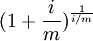的極限為e,即
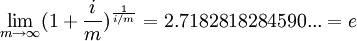
所以當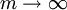連續複利本利和公式為：
![p_n=\lim_{m \to \infty}p_0(1+\frac{i}{m})^{mn}=p_0\lim_{m \to \infty}[(1+\frac{i}{m})^{\frac{1}{i/m}}]^{ni}=p_0e^{ni}](/w/images/math/0/1/a/01a495c66a0dfd53c58e930663ed2c09.png)
(1)
即：
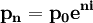
式中eni成為瞬間複利繫數，或稱一元錢的瞬間複利本利和
- 連續複利收益率（Continuously compounded rate of return，CCR）
- 年度百分率(annual percentage rate,APR)
- 有效年利率（Effective Annual Rates，EAR)
- T為持有期
短期投資利率常用APR來表示，一年有n=1/T期，每期利率為RT,則
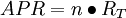
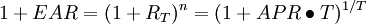
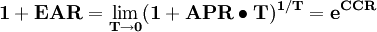
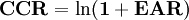
評論(共13條)
e怎麼得出的？
添加和修改了部分內容，希望對你有幫助~
連續複利涉及的利率轉化問題 若Rc表示連續複利的利率，Rm表示一年計m次利息的利率， 則 滿足等式 （1+Rm／m）^m=e^Rc 可求得， Rc=m（ln（Rm／m）+1） Rm=m（e^(Rc／m）-1）
在實際生活中，有這種演算法嗎? 在實際生活中，利率，用款時間都是雙方商定的。能有這種縮短計算周期、為一方提高效益的單相思地計算利息收益的應用嗎? 這是不存在的，原因是這種推導即違反數學思維，又違背實際生活。
e怎麼得出的？
e是一個常數。是有一個數學家很無聊(>ω<)，不知道是用筆算還是計算器算出來的，當x無限大的時候，那個函數不會增長，而是等於一個常數，你可以拿計算器就可以算出這個數字
e怎麼得出的？