有效年利率

出自 MBA智库百科(https://wiki.mbalib.com/)

有效年利率(Effective Annual Rate，EAR)

　　有效年利率指在按照給定的計息期利率和每年複利次數計算利息時，能夠產生相同結果的每年複利一次的年利率。

　　計算公式為：

　　EAR = (1 + r / m)^m − 1

　　其中

• EAR為有效年利率，
• r為名義利率，
• m為一年內計息次數。

• 年度百分率(Annual Percentage Rate,APR)
• 有效年利率（Effective Annual Rates，EAR)
• T為持有期
• r為名義利率(APR)
• m為一年內計息次數

　　短期投資利率常用APR來表示，一年有m期(m=1/T)，每期利率為R_T(R_T=r/m),則

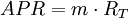
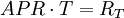
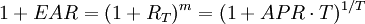
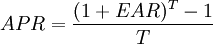
　　1 + EAR = (1 + HPR)^{1 / T}

　　其中

• EAR為有效年利率
• T為持有期
• HPR為持有期收益率(Holding Period Return)

　　某債券的名義年利率為8%，每年支付利息兩次(年複利次數為2)，則其有效年利率為多少？

　　可以看到，有效年利率大於名義年利率。如果年複利次數越多，那麼有效年利率越大。我們可以算出m=4和m=12時的EAR，如下：

　　EAR = (1 + 8% / 4)⁴ − 1 = 0.0824 = 8.24%

　　EAR = (1 + 8% / 12)¹² − 1 = 0.0830 = 8.30%

　　如果年複利次數非常非常多(複利期間非常非常短)，那麼EAR是否趨近於無窮大呢?我們說如果m趨向於正無窮，EAR並不趨近於無窮大，而是趨近於e^{名義年利率}-1。我們稱之為連續複利(continuous compounding)。在上例中，如果每年複利無窮多次，EAR = e^0.08 − 1 = 0.0833 = 8.33%。這裡的e是自然對數底，是一個常數，約等於2．718。