有效年利率
出自 MBA智库百科(https://wiki.mbalib.com/)
有效年利率(Effective Annual Rate,EAR)
目录 |
有效年利率指在按照给定的计息期利率和每年复利次数计算利息时,能够产生相同结果的每年复利一次的年利率。
计算公式为:
EAR = (1 + r / m)m − 1
其中
短期投资利率常用APR来表示,一年有m期(m=1/T),每期利率为RT(RT=r/m),则
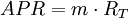
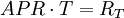
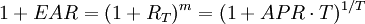
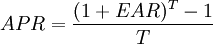
1 + EAR = (1 + HPR)1 / T
其中
- EAR为有效年利率
- T为持有期
- HPR为持有期收益率(Holding Period Return)
案例一:[1]
某债券的名义年利率为8%,每年支付利息两次(年复利次数为2),则其有效年利率为多少?

可以看到,有效年利率大于名义年利率。如果年复利次数越多,那么有效年利率越大。我们可以算出m=4和m=12时的EAR,如下:
EAR = (1 + 8% / 4)4 − 1 = 0.0824 = 8.24%
EAR = (1 + 8% / 12)12 − 1 = 0.0830 = 8.30%
如果年复利次数非常非常多(复利期间非常非常短),那么EAR是否趋近于无穷大呢?我们说如果m趋向于正无穷,EAR并不趋近于无穷大,而是趋近于e名义年利率-1。我们称之为连续复利(continuous compounding)。在上例中,如果每年复利无穷多次,EAR = e0.08 − 1 = 0.0833 = 8.33%。这里的e是自然对数底,是一个常数,约等于2.718。
- ↑ 林晨雷著.第一章 货币时间价值 破解CFA定量方法.中国财政经济出版社,2012.01.








能否稍微解释下 这个有效年利率和本身债券给定的收益率之间的联系 真是购买债券时候计算 expected rate of return时候为什么要用有效年利率?
比如一个bond 每年之只计息一次的话 那为什么不按照给定的bond的收益率 而要转换成有效年利率?