复利
出自 MBA智库百科(https://wiki.mbalib.com/)
复利(Compound Interest)
目录 |
复利是与单利相对应的经济概念。单利的计算不用把利息计入本金;而复利恰恰相反,它的利息要并入本金中重复计息。复利就是复合利息,它是指每年的收益还可以产生收益,具体是将整个借贷期限分割为若干段,前一段按本金计算出的利息要加入到本金中,形成增大了的本金,作为下一段计算利息的本金基数,直到每一段的利息都计算出来,加总之后,就得出整个借贷期内的利息,简单来说就是俗称的利滚利。有人甚至称其为“世界第八大奇观”。
从定义上可以看出复利的要素有三个:初始本金、报酬率和时间。
复利计算的特点是:把上期未的本利和作为下一期的本金,在计算时每一期本金的数额是不同的。复利的计算公式是:S = P(I + i)n,其中以符号I代表利息,P代表本金,n代表期数,i代表利率,S代表本利和。
复利的报酬惊人,比方说拿10万元去买年报酬率20%的股票,约莫3年半的时间,10万元就变成20万元。复利的时间乘数效果,更是这其中的奥妙所在。
复利的力量是巨大的。印度有个古老故事,国王与象棋国手下棋输了,国手要求在第一个棋格中放上一粒麦子,第二格放上两粒,第三格放上四粒,即按复利增长的方式放满整个棋格。国王以为这个棋手可以得到一袋麦子,结果却是全印度的麦子都不足以支付。
所以,追逐复利的力量,正是资本积累的动力。
1、复利终值
复利终值是指本金在约定的期限内获得利息后,将利息加入本金再计利息,逐期滚算到约定期末的本金之和。
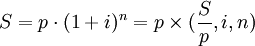
其中:(1+i)n 被称为复利终值系数,符号用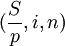 表示。
表示。
例如:本金为50000元,利率或者投资回报率为3%,投资年限为30年,那么,30年后所获得的利息收入,按复利计算公式来计算就是:50000×(1 + 3%)30
由于,通胀率和利率密切关联,就像是一个硬币的正反两面,所以,复利终值的计算公式也可以用以计算某一特定资金在不同年份的实际价值。只需将公式中的利率换成通胀率即可。
2、复利现值
复利现值是指在计算复利的情况下,要达到未来某一特定的资金金额,现在必须投入的本金。
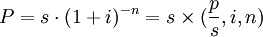
其中:(1 + i) − n被称为复利现值系数,符号用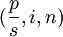 表示。
表示。
例如:30年之后要筹措到300万元的养老金,假定平均的年回报率是3%,那么,现在必须投入的本金是3000000×1/(1 + 3%)30
评论(共17条)
compounded rate can also be divided into 'discretely compounded rate' and 'continuously compounded rate'. they have different calculation methods, anyone can explain that further?
这个公式有误吧?
”复利的计算公式是:S = P(I + i)^n,其中以符号I代表利息,P代表本金,n代表时期,i代表利率,S代表本利和。“
最后一句中公式也写错了?没有X1的存在吧?
“现在必须投入的本金是3000000×1/(1 + 3%)^30”
这个公式有误吧?
”复利的计算公式是:S = P(I + i)^n,其中以符号I代表利息,P代表本金,n代表时期,i代表利率,S代表本利和。“
最后一句中公式也写错了?没有X1的存在吧?
“现在必须投入的本金是3000000×1/(1 + 3%)^30”
公式里是"^-n", 所以是乘以1分之balabala^30,对的
复利是与单利相对应的经济概念。单利的计算不用把利息计入本金;而复利恰恰相反,它的利息要并入本金中重复计息。








不错