终值
出自 MBA智库百科(https://wiki.mbalib.com/)
终值(future value)
目录 |
终值又称将来值或本利和,是指现在一定量的资金在将来某个时点上的价值。
在日常生活中有许多属于终值计算的问题。例如,张先生最近购买彩票,中奖100000元,他想将这笔钱存入银行,以便将来退休时抵用,设张先生还有10年退休,如按年存款利率2%计算,10年后张先生退休时能拿多少钱?
- (一)单利的计算
设现有一笔资金,共计金额为P,存期为n年,年利率为i,则n年后的终值FVn为:
FVn=P+P·i·n=P(1+i·n)
上例中,张先生退休能拿的本利和为100000×(1+2%×10)=120000元。
- (二)复利的计算
设现有一笔资金,共计金额为P,存期为n年,年利率为i,则n年后的终值FVn为:
第1年年末的本利和为P(1+i)
第2年年末的本利和为P(1 + i) + P(1 + i)i = P(1 + i)2
第3年年末的本利和为P(1 + i)2 + P(1 + i)2i = P(1 + i)3
……
第n年年末的本利和为P(1 + i)n
因此,FVn = P(1 + i)n
式中,(1 + i)n在财务管理学上称为复利终值系数,我们用FVIFi,n表示,它是计算复利终值的主要参数。其中i是计算货币价值的利息率,n是货币到期长度。人们可以用专门的程序在电子计算机中计算出来,以避免手工计算麻烦。
上例中,如果按复利计算,则张先生10年后退休可获得
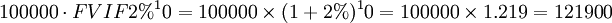 元。
元。
评论(共4条)
在下虽然数学方面极不善,敢问上文中以下公式是否有误呢?
“第2年年末的本利和为P(1 + i) + P(1 + i)i = P(1 + i)2”
“第3年年末的本利和为P(1 + i)2 + P(1 + i)2i = P(1 + i)3”
中间的P(1 + i)i,利率的平方?实在不明。 ----- Umbrella Revolution
这个公式应该是本利和为 P(1 + i) + P(1 + i)i = P(1 + i)(1 + i)=P(1 + i)^2,求出则得出利率的平方,公式没有错误呀
在下虽然数学方面极不善,敢问上文中以下公式是否有误呢?
“第2年年末的本利和为P(1 + i) + P(1 + i)i = P(1 + i)2”
“第3年年末的本利和为P(1 + i)2 + P(1 + i)2i = P(1 + i)3”
中间的P(1 + i)i,利率的平方?实在不明。 ----- Umbrella Revolution
其实第二年就是等于第一年 X (1+i) 也就是第一年 P (1 + i) 第二年 P (1 + i) (1 + 1) = P (1 + i )^2
在下虽然数学方面极不善,敢问上文中以下公式是否有误呢?
“第2年年末的本利和为P(1 + i) + P(1 + i)i = P(1 + i)2”
“第3年年末的本利和为P(1 + i)2 + P(1 + i)2i = P(1 + i)3”
中间的P(1 + i)i,利率的平方?实在不明。 ----- Umbrella Revolution
哈哈哈哈,你的数学确实极为不善








在下虽然数学方面极不善,敢问上文中以下公式是否有误呢?
“第2年年末的本利和为P(1 + i) + P(1 + i)i = P(1 + i)2”
“第3年年末的本利和为P(1 + i)2 + P(1 + i)2i = P(1 + i)3”
中间的P(1 + i)i,利率的平方?实在不明。 ----- Umbrella Revolution