連續複利收益率
出自 MBA智库百科(https://wiki.mbalib.com/)
連續複利收益率(Continuously Compounded Rate of Return，CCR)
目錄 |
連續複利收益率概述[1]
為介紹連續複利收益率的概念，首先討論複利次數與期末總資金間的關係。在單期 內，複利計息的次數愈多，期末總資金的累積也愈大，說明如下：
若年收益率為14％，1000元資金投資兩年後的期末資金應為：
1000(1＋14％)2 ＝ 1299.６(元)
若每年內複利生息２次(每六個月複利一次),則期終資金為：
1000(１＋14％/2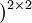
＝1301.８(元)
若每年內複利生息4次，則期終資金為：
1000(１＋14％/4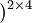
＝1316.８(元)
所以，若以R代表年利率，m代表每期(每年)內的複利次數，n代表投資期限(n年)，則以C0元投資n期(年)後所得的期末資金應為：
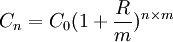
式中，R／m代表小期內(In Asub-Period)的收益率。根據上式，可以分析連續複利收益率的概念以及計算方法。若將單一期(１年)內的複利次數(m)增加，則投資收益將會以更快的速度複利生息。也就是說，在單一期內複利生息的次數愈多，計算複利的期間也就愈縮短。當複利次數增至無限大時(m→∞)，投資收益將在每一瞬息間複利生息。這種瞬息複利生息的複利稱為連複利生息(Continuously Compounding)。那麼連續複利會不會導致期末資金的無限大？運用高等數學的極限知識，有：
![\lim_{m\to \infty} (1+\frac{R}{m})^{nm}=\lim_{m\to \infty} [(1+\frac{1}{m/R})^{m/R}]^{nR}=e^{nR}](/w/images/math/4/4/6/4468da078175a44c90074e0b908ed03d.png)
所以，在持續複利生息下，C0元投資n期(年)後所得的期末資金應為：
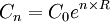
反之，假設R代表單一期收益率，能與單期複利生息產生相同期終資金的連續複利 報酬率R′應為：
R′=ln(1＋R) (1)
此處，ln代表自然對數函數，證明如下：
以C0元投資一期，並複利計息一次的期末資金為：
C1 = C0(1 + R) (2)
以連續複利生息一期所得的期終資金應為
C1 = C0eR' (3)
(2)式等於(3)式，可得(1)式。所以，若單期收益率為R，則其對等的連續複利收益率應為(1＋R)的自然對數，即ln(1＋R)。
連續複利收益率在投資研究的領域中運用十分廣泛。其原因之一在於，它的概率分佈較接近於正態分佈，對金融經濟學的理論發展與實際驗證的簡化具有相當大的幫助。
- 連續複利收益率（Continuously compounded rate of return，CCR）
- 年度百分率(annual percentage rate,APR)
- 有效年利率（Effective Annual Rates，EAR)
- T為持有期
短期投資利率常用APR來表示，一年有n=1/T期，每期利率為RT,則
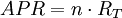
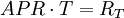
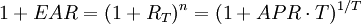
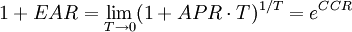
CCR = ln(1 + EAR)
- ↑ 孫伍琴,王朝暉,熊樂星.證券投資學.上海市：立信會計出版社,2008.
