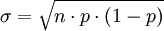概率分佈
出自 MBA智库百科(https://wiki.mbalib.com/)
概率分佈(Probability Distribution)
目錄 |
概率分佈是指隨機變數X小於任何已知實數x的事件可以表示成的函數。用以表述隨機變數取值的概率規律。描述不同類型的隨機變數有不同的概率分佈形式。是概率論的基本概念之一。
離散型隨機變數的分佈列只取有限個或可列個實數值的隨機變數稱為離散型隨機變數。例如,100件產品中有10件次品,從中隨意抽取5件,則其中的次品數X就是一個只取0,1,2,3,4,5的離散型隨機變數。描述離散型隨機變數的概率分佈使用分佈列,即給出離散型隨機變數的全部取值,及取每個值的概率。例如上面例子中次品數X的分佈列為:其中,表示從n個不同事物中取m個的組合數:
概率分佈第一行寫出隨機變數X的取值,第二行列出取相應值的概率。這就是X的分佈列。常見的離散型隨機變數的分佈有單點分佈、兩點分佈、正態分佈、二項分佈、幾何分佈、負二項分佈、超幾何分佈、泊松分佈等。
概率分佈(probabilitydistribution)或簡稱分佈(distribution),是概率論的一個概念。使用時可以有以下兩種含義:
廣義地,概率分佈是指稱隨機變數的概率性質:當我們說概率空間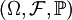 中的兩個隨機變數X和Y具有同樣的分佈(或同分佈)時,我們是無法用概率
中的兩個隨機變數X和Y具有同樣的分佈(或同分佈)時,我們是無法用概率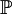 來區別他們的。換言之:稱X和Y為同分佈的隨機變數,當且僅當對任意事件
來區別他們的。換言之:稱X和Y為同分佈的隨機變數,當且僅當對任意事件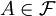 ,有
,有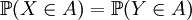 成立。
成立。
但是,不能認為同分佈的隨機變數是相同的隨機變數。事實上即使X與Y同分佈,也可以沒有任何點ω使得X(ω)=Y(ω)。在這個意義下,可以把隨機變數分類,每一類稱作一個分佈,其中的所有隨機變數都同分佈。用更簡要的語言來說,同分佈是一種等價關係,每一個等價類就是一個分佈。需註意的是,通常談到的離散分佈、均勻分佈、伯努利分佈、正態分佈、泊松分佈等,都是指各種類型的分佈,而不能視作一個分佈。
狹義地,它是指隨機變數的概率分佈函數。設X是樣本空間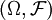 上的隨機變數,
上的隨機變數,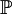 為概率測度,則稱如下定義的函數是X的分佈函數(distribution function),或稱累積分佈函數(cumulative distribution function,簡稱CDF):
為概率測度,則稱如下定義的函數是X的分佈函數(distribution function),或稱累積分佈函數(cumulative distribution function,簡稱CDF):
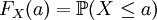 ,對任意實數a定義。
,對任意實數a定義。
具有相同分佈函數的隨機變數一定是同分佈的,因此可以用分佈函數來描述一個分佈,但更常用的描述手段是概率密度函數(probability density function,pdf)。
對於特定的隨機變數X,其分佈函數FX是單調不減及右連續,而且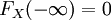 ,
,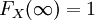 。這些性質反過來也描述了所有可能成為分佈函數的函數數:
。這些性質反過來也描述了所有可能成為分佈函數的函數數:
設![F[-\infty,\infty]\to[0,1],F(-\infty)=0,F(\infty)=1](/w/images/math/9/0/b/90b383023eb43a4e8da1f4c1f97d29da.png) 且單調不減、右連續,則存在概率空間
且單調不減、右連續,則存在概率空間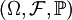 及其上的隨機變數X,使得F是X的分佈函數,即FX = F
及其上的隨機變數X,使得F是X的分佈函數,即FX = F
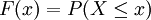 (
(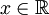 )
)
稱為X的概率分佈函數.如果將X看成是數軸上的隨機點的坐標,那麼,分佈函數F(x)在x處的函數值就表示X落在區間(-∞,x]上的概率。
例如,設隨機變數X為擲兩次骰子所得的點數差,而整個樣本空間由36個元素組成,
| 數量 | ( i , j )∈ S | x | P(X = x) | F(x) |
|---|---|---|---|---|
| 6 | ( 1,1 ),( 2,2 ),( 3,3 ) ( 4,4 ),( 5,5 ),( 6,6 ) | 0 | 6/36 | 6/36 |
| 10 | ( 1,2 ),( 2,3 ) ( 3,4 ),( 4,5 ),( 5,6 ) ( 2,1 ),( 3,2 ),( 4,3 ) ( 5,4 ),( 6,5 ) | 1 | 10/36 | 16/36 |
| 8 | ( 1,3 ),( 2,4 ),( 3,5 ) ( 4,6 ),( 3,1 ),( 4,2 ) ( 5,3 ),( 6,4 ) | 2 | 8/36 | 24/36 |
| 6 | ( 1,4 ),( 2,5 ),( 3,6 ) ( 4,1 ),( 5,2 ),( 6,3 ) | 3 | 6/36 | 30/36 |
| 4 | ( 1,5 ),( 2,6 ) ( 5,1 ),( 6,2 ) | 4 | 4/36 | 34/36 |
| 2 | ( 1,6 ),( 6,1 ) | 5 | 2/36 | 36/36 |
其分佈函數是:
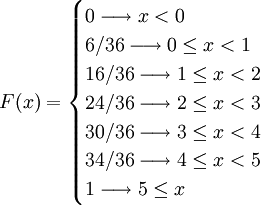
上面所列舉的例子都屬於離散分佈,即分佈函數的值域是離散的,比如只取整數值的隨機變數就是屬於離散分佈的。F(x)表示隨機變數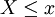 的概率值。如果X的取值只有x1 < x2 < ... < xn,則:
的概率值。如果X的取值只有x1 < x2 < ... < xn,則:
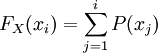
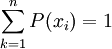
二項分佈是最重要的離散概率分佈之一,由瑞士數學家雅各布·伯努利(Jokab Bernoulli)所發展,一般用二項分佈來計算概率的前提是,每次抽出樣品後再放回去,並且只能有兩種試驗結果,比如黑球或紅球,正品或次品等。二項分佈指出,隨機一次試驗出現的概率如果為p,那麼在n次試驗中出現k次的概率為:
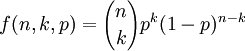
例如,在擲3次骰子中,不出現6點的概率是: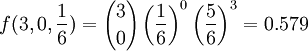
在連續兩次的輪盤游戲中,至少出現一次紅色的概率為: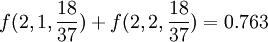
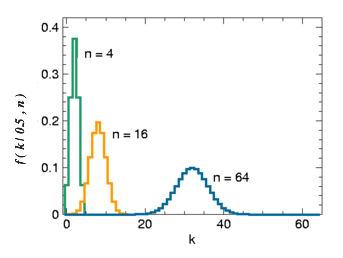
二項分佈在p = 0.5時表現出圖像的對稱性,而在p取其它值時是非對稱的。另外二項分佈的期望值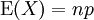 ,以及方差
,以及方差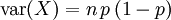
在離散分佈中如果試驗次數n值非常大,而且單次試驗的概率p值又不是很小的情況下,正態分佈可以用來近似的代替二項分佈。一個粗略的使用正態分佈的近似規則是: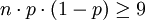 。
。
從二項分佈中獲得μ和σ值的方法是
期望值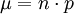
如果σ > 3,則必須採用下麵的近似修正方法:
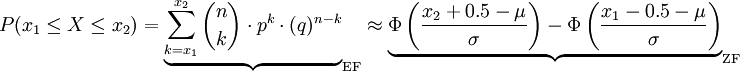
註:q = 1 − p,EF:二項分佈,ZF:正態分佈)
上(下)臨界值分別增加(減少)修正值0.5的目的是在σ值很大時獲得更精確的近似值,只有σ很小時,修正值0.5可以不被考慮。
例如,隨機試驗為連續64次擲硬幣,獲得的國徽數位於32和42之間的概率是多少?用正態分佈計算如下,
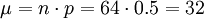
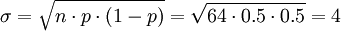
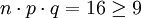 ,符合近似規則,應用z-變換:
,符合近似規則,應用z-變換:
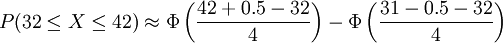
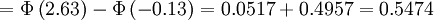
在運用z表格時註意到利用密度函數的對稱性來求出z為負值時的區域面積。
作為離散概率分佈的超幾何分佈尤其指在抽樣試驗時抽出的樣品不再放回去的分佈情況。在一個容器中一共有N個球,其中M個黑球,(N − M)個紅球,通過下麵的超幾何分佈公式可以計算出,從容器中抽出的n個球中(抽出的球不放回去)有k個黑球的概率是多少:
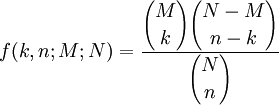
例如,容器中一共10個球,其中6個黑色,4個白色,一共抽5次(抽出的球不放回去),在這5個球中有3個黑球的概率是:
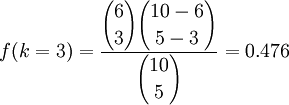
和二項分佈不同的是,在超幾何分佈中,特別強調的是抽出的樣品在下一次抽取前不再放回去,但是如果抽取的次數n和總共樣品數N相比很小(大約n / N < 0,05),這時在計算上二項分佈和超幾何分佈相互間則沒有主要的區別,此時人們更願意採用二項分佈的方法,因為在數學計算上二項分佈要簡單一些。
泊松近似是二項分佈的一種極限形式。其強調如下的試驗前提:一次抽樣的概率值p相對很小,而抽取次數n值又相對很大。因此泊松分佈又被稱之為罕有事件分佈。泊松分佈指出,如果隨機一次試驗出現的概率為p,那麼在n次試驗中出現k次的概率按照泊松分佈應該為:
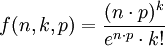
其中數學常數e = 2.71828...(自然對數的底數)
例如,某工廠在生產零件時,每200個成品中會有1個次品,那麼在100個零件中最多出現2個次品的概率按照泊松分佈應該是:
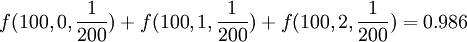
在實踐中如果遇到n值很大導致二項分佈難於計算時,可以考慮使用泊松分佈,但前提是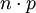 必須趨於一個有限極限。採用泊松分佈的一個不太嚴格的規則是:
必須趨於一個有限極限。採用泊松分佈的一個不太嚴格的規則是:

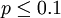
設X是具有分佈函數F的連續隨機變數,且F的一階導數處處存在,則其導函數
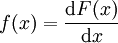
稱為X的機率密度函數。
每個機率密度函數都有如下性質:
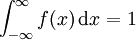
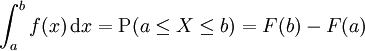
第一個性質表明,機率密度函數與x軸形成的區域的面積等於1,第二個性質表明,連續隨機變數在區間[ab]的概率值等於密度函數在區間[ab]上的積分,也即是與X軸在[ab]內形成的區域的面積。因為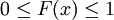 ,且f(x)是Fx)的導數,因此按照積分原理不難推出上面兩個公式。
,且f(x)是Fx)的導數,因此按照積分原理不難推出上面兩個公式。
正態分佈和指數分佈t-分佈,F-分佈以及ξ2-分佈都是連續分佈。
連續隨機變數的機率密度函數如果是如下形式,
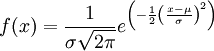
那麼這個連續分佈被稱之為正態分佈,或者高斯分佈。其密度函數的曲線呈對稱鐘形,因此又被稱之為鐘形曲線,其中μ是平均值,σ是標準差。正態分佈是一種理想分佈,許多典型的分佈,比如成年人的身高,汽車輪胎的運轉狀態,人類的智商值(IQ),都屬於或者說至少接近正態分佈。同樣按照連續分佈的定義,正態機率密度函數具有和普通機率密度函數類似的性質:
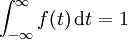
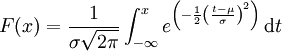
如果給出一個正態分佈的平均值μ以及標準差σ,可以根據上面的第二個公式計算出任一區間的概率分佈情況。但是如上的計算量是相當龐大的,沒有電腦的輔助基本是不可能的,解決這一問題的方法是藉助z-變換以及標準正態分佈表格(z-表格)。
中間值μ = 0以及標準差σ = 1的正態分佈被稱之為標準正態分佈,其累積分佈函數是
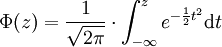
將普通形式的正態分佈變換到標準正態分佈的方法是
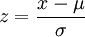
例如,已知一正態分佈的μ = 5,σ = 3,求區間概率值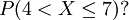 計算過程如下,
計算過程如下,
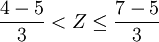
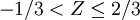
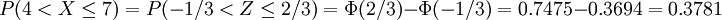
其中Φ(z)值通過查z-表格獲得。