伯努利分佈
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
[編輯]
伯努利分佈是指一個分佈離散型概率分佈，為紀念瑞士科學家雅各布布•伯努利而命名。若伯努利試驗成功，則伯努利隨機變數取值為1。若伯努利試驗失敗，則伯努利隨機變數取值為0。
[編輯]
伯努利試驗成功概率為
，失敗概率為q = 1 − p。則其概率質量函數為：
其期望值為：
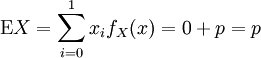
其方差為：
![\operatorname{var}X = \sum_{i=0}^1(x_i-E[X])^2f_X(x)= (0-p)^2(1-p) + (1-p)^2p = p(1-p) = pq](/w/images/math/5/8/2/58282c3421bbe6aa572466e57679b36e.png)
