離散型隨機變數
出自 MBA智库百科(https://wiki.mbalib.com/)
離散型隨機變數(Discrete Type Random Variable)
目錄 |
什麼是離散型隨機變數[1]
設X是一個隨機變數,如果它全部可能的取值只有有限個或可數無窮個,則稱X為一個離散型隨機變數。
設X1,X2,…是隨機變數X的所有可能取值,對每個取值Xi,X = xi是其樣本空間S上的一個事件,為描述隨機變數X,還需知道這些事件發生的可能性(概率)。
定義1 設離散型隨機變數X的所有可能取值為xi(i=1,2,…),
P(X = xi) = Pi,i = 1,2,...
稱為X的概率分佈或分佈律,也稱概率函數。
常用表格形式來表示X的概率分佈:
| X | x1 | x2 | ... | xn | ... |
| Pi | p1 | p2 | ... | pn | ... |
由概率的定義,Pi(i = 1,2,...)必然滿足:
(1)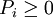 ,i=1, 2, …;
,i=1, 2, …;
| ∑ | Pi = 1 |
| i |
【例1】 某籃球運動員投中籃圈的概率是0.9,求他兩次獨立投籃投中次數X的概率分佈.[2]
解 X可取0,1,2為值,記Ai={第i次投中籃圈},i=1,2,則P(A1) = P(A2) = 0.9
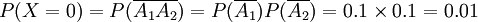
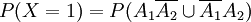
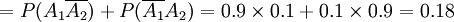 ,
,
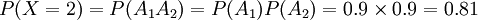 ,
,
且 PX = 0 + PX = 1 + Px = 2 = 1
於是,X的概率分佈可表示為
| X | 0 | 1 | 2 |
| P_i | 0.01 | 0.18 | 0.81 |
關於分佈律的說明
若已知一個離散型隨機變數X的概率分佈:
| X | x_1 | x_2 | ... | x_n | ... |
| P_i | p_1 | p_2 | ... | p_n | ... |
則可以求得X所生成的任何事件的概率,特別地,
 ,
,
例如,設X的概率分佈由例1給出,則
P{x<2}=P{x=0}+P{X=l}=0.0l+0.18=0.19
P{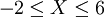 }=P{X=0}+P{X=1}+P{X=2}=1
}=P{X=0}+P{X=1}+P{X=2}=1
常見的離散型隨機變數的分佈[3]
(1)兩點分佈(0-1分佈)
若隨機變數X只可能取0和1兩個值,且它的分佈列為P{X=1}=p,PX = 0 = l − P(0 < P < 1),則稱X服從參數為p的兩點分佈,記作X~B(1, p)。其分佈函數為
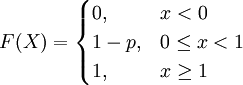
(2)二項分佈
若隨機變數X的分佈律為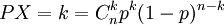 (k=0, 1, 2, ..., n) 且0<P<1,則稱X服從參數為n,P的二項分佈,記作x~B(n,P)。
(k=0, 1, 2, ..., n) 且0<P<1,則稱X服從參數為n,P的二項分佈,記作x~B(n,P)。
(3)泊松(Poisson)分佈
若隨機變數X所有可能取值為0,1,2,…,它取各個值的概率為
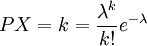 ,(k=0,1,2,…)
,(k=0,1,2,…)
式中:λ > 0是常數,則稱X服從參數為 λ 的泊松分佈,記為X ~ Π(λ)。








謝謝,例子舉得很明白