資本資產定價模型
出自 MBA智库百科(https://wiki.mbalib.com/)
資本資產定價模型(Capital Asset Pricing Model,CAPM)
目錄 |
CAPM模型的提出[1]
馬科維茨(Markowitz,1952)的分散投資與效率組合投資理論第一次以嚴謹的數理工具為手段向人們展示了一個風險厭惡的投資者在眾多風險資產中如何構建最優資產組合的方法。應該說,這一理論帶有很強的規範(normative)意味,告訴了投資者應該如何進行投資選擇。但問題是,在20世紀50年代,即便有了當時剛剛誕生的電腦的幫助,在實踐中應用馬科維茨的理論仍然是一項煩瑣、令人生厭的高難度工作;或者說,與投資的現實世界脫節得過於嚴重,進而很難完全被投資者採用——美國普林斯頓大學的鮑莫爾(william Baumol)在其1966年一篇探討馬科維茨一托賓體系的論文中就談到,按照馬科維茨的理論,即使以較簡化的模式出發,要從1500只證券中挑選出有效率的投資組合,當時每運行一次電腦需要耗費150~300美元,而如果要執行完整的馬科維茨運算,所需的成本至少是前述金額的50倍;而且所有這些還必須有一個前提,就是分析師必須能夠持續且精確地估計標的證券的預期報酬、風險及相關係數,否則整個運算過程將變得毫無意義。
正是由於這一問題的存在,從20世紀60年代初開始,以夏普(w.Sharpe,1964),林特納(J.Lintner,1965)和莫辛(J.Mossin,1966)為代表的一些經濟學家開始從實證的角度出發,探索證券投資的現實,即馬科維茨的理論在現實中的應用能否得到簡化?如果投資者都採用馬科維茨資產組合理論選擇最優資產組合,那麼資產的均衡價格將如何在收益與風險的權衡中形成?或者說,在市場均衡狀態下,資產的價格如何依風險而確定?
這些學者的研究直接導致了資本資產定價模型(capital asset pricing model,CAPM)的產生。作為基於風險資產期望收益均衡基礎上的預測模型之一,CAPM闡述了在投資者都採用馬科維茨的理論進行投資管理的條件下市場均衡狀態的形成,把資產的預期收益與預期風險之間的理論關係用一個簡單的線性關係表達出來了,即認為一個資產的預期收益率與衡量該資產風險的一個尺度β值之間存在正相關關係。應該說,作為一種闡述風險資產均衡價格決定的理論,單一指數模型,或以之為基礎的CAPM不僅大大簡化了投資組合選擇的運算過程,使馬科維茨的投資組合選擇理論朝現實世界的應用邁進了一大步,而且也使得證券理論從以往的定性分析轉入定量分析,從規範性轉入實證性,進而對證券投資的理論研究和實際操作,甚至整個金融理論與實踐的發展都產生了巨大影響,成為現代金融學的理論基礎。
當然,近幾十年,作為資本市場均衡理論模型關註的焦點,CAPM的形式已經遠遠超越了夏普、林特納和莫辛提出的傳統形式,有了很大的發展,如套利定價模型、跨時資本資產定價模型、消費資本資產定價模型等,目前已經形成了一個較為系統的資本市場均衡理論體系。
夏普發現單個股票或者股票組合的預期回報率(Expected Return)的公式如下:
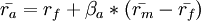
其中,rf(Risk free rate),是無風險回報率,純粹的貨幣時間價值;
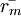 是市場期望回報率 (Expected Market Return),
是市場期望回報率 (Expected Market Return),
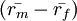 是股票市場溢價 (Equity Market Premium).
是股票市場溢價 (Equity Market Premium).
CAPM公式中的右邊第一個是無風險收益率,比較典型的無風險回報率是10年期的美國政府債券。如果股票投資者需要承受額外的風險,那麼他將需要在無風險回報率的基礎上多獲得相應的溢價。那麼,股票市場溢價(equity market premium)就等於市場期望回報率減去無風險回報率。證券風險溢價就是股票市場溢價和一個β繫數的乘積。
CAPM是建立在馬科威茨模型基礎上的,馬科威茨模型的假設自然包含在其中:
1、投資者希望財富越多愈好,效用是財富的函數,財富又是投資收益率的函數,因此可以認為效用為收益率的函數。
4、影響投資決策的主要因素為期望收益率和風險兩項。
5、投資者都遵守主宰原則(Dominance rule),即同一風險水平下,選擇收益率較高的證券;同一收益率水平下,選擇風險較低的證券。
CAPM的附加假設條件:
6、可以在無風險折現率R的水平下無限制地借入或貸出資金。
7、所有投資者對證券收益率概率分佈的看法一致,因此市場上的效率邊界只有一條。
8、所有投資者具有相同的投資期限,而且只有一期。
9、所有的證券投資可以無限制的細分,在任何一個投資組合里可以含有非整數股份。
11、所有投資者可以及時免費獲得充分的市場信息。
13、投資者具有相同預期,即他們對預期收益率、標準差和證券之間的協方差具有相同的預期值。
上述假設表明:第一,投資者是理性的,而且嚴格按照馬科威茨模型的規則進行多樣化的投資,並將從有效邊界的某處選擇投資組合;第二,資本市場是完美/完全市場,沒有任何磨擦阻礙投資。
- 優點
CAPM最大的優點在於簡單、明確。它把任何一種風險證券的價格都劃分為三個因素:無風險收益率、風險的價格和風險的計算單位,並把這三個因素有機結合在一起。
CAPM的另一優點在於它的實用性。它使投資者可以根據絕對風險而不是總風險來對各種競爭報價的金融資產作出評價和選擇。這種方法已經被金融市場上的投資者廣為採納,用來解決投資決策中的一般性問題。
- 局限性
當然,CAPM也不是盡善盡美的,它本身存在著一定的局限性。表現在:
首先,CAPM的假設前提是難以實現的。比如,在本節開頭,我們將CAPM的假設歸納為六個方面。假設之一是市場處於完善的競爭狀態。但是,實際操作中完全競爭的市場是很難實現的,“做市”時有發生。假設之二是投資者的投資期限相同且不考慮投資計劃期之後的情況。但是,市場上的投資者數目眾多,他們的資產持有期間不可能完全相同,而且現在進行長期投資的投資者越來越多,所以假設二也就變得不那麼現實了。假設之三是投資者可以不受限制地以固定的無風險利率借貸,這一點也是很難辦到的。假設之四是市場無摩擦。但實際上,市場存在交易成本、稅收和信息不對稱等等問題。假設之五、六是理性人假設和一致預期假設。顯然,這兩個假設也只是一種理想狀態。
其次,CAPM中的β值難以確定。某些證券由於缺乏歷史數據,其β值不易估計。此外,由於經濟的不斷發展變化,各種證券的β值也會產生相應的變化,因此,依靠歷史數據估算出的β值對未來的指導作用也要打折扣。總之,由於CAPM的上述局限性,金融市場學家仍在不斷探求比CAPM更為準確的資本市場理論。目前,已經出現了另外一些頗具特色的資本市場理論(如套利定價模型),但尚無一種理論可與CAPM相匹敵。
按照CAPM的規定,Beta繫數是用以度量一項資產系統風險的指針,是用來衡量一種證券或一個投資組合相對總體市場的波動性(volatility)的一種風險評估工具。也就是說,如果一個股票的價格和市場的價格波動性是一致的,那麼這個股票的Beta值就是1。如果一個股票的Beta是1.5,就意味著當市場上升10%時,該股票價格則上升15%;而市場下降10%時,股票的價格亦會下降15%。
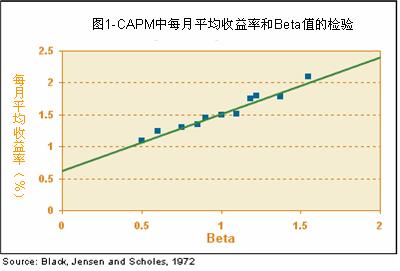
Beta是通過統計分析同一時期市場每天的收益情況以及單個股票每天的價格收益來計算出的。1972年,經濟學家費歇爾·布萊克 (Fischer Black)、邁倫·斯科爾斯(Myron Scholes)等在他們發表的論文《資本資產定價模型:實例研究》中,通過研究1931年到1965年紐約證券交易所股票價格的變動,證實了股票投資組合的收益率和它們的Beta間存在著線形關係。
當Beta值處於較高位置時,投資者便會因為股份的風險高,而會相應提升股票的預期回報率。舉個例子,如果一個股票的Beta值是2.0,無風險回報率是3%,市場回報率(Market Return)是7%,那麼市場溢價(Equity Market Premium) 就是4%(7%-3%),股票風險溢價(Risk Premium)為8% (2X4%,用Beta值乘市場溢價),那麼股票的預期回報率則為11%(8%+3%, 即股票的風險溢價加上無風險回報率)。
以上的例子說明,一個風險投資者需要得到的溢價可以通過CAPM計算出來。換句話說,我們可通過CAPM來知道當前股票的價格是否與其回報相吻合。
2.資產風險溢酬=風險的價格×風險的數量
3.風險的數量 = β(SML的斜率)。
4.風險的價格 = E(Rm) − Rf
5.證券市場線(SML)的斜率等於市場風險貼水,當投資人的風險規避程度愈高,則SML的斜率愈大,證券的風險溢酬就愈大,證券的要求報酬率也愈高。
6.當證券的系統性風險(用β來衡量)相同,則兩者之要求報酬率亦相同,證券之單一價格法則。
CAPM給出了一個非常簡單的結論:只有一種原因會使投資者得到更高回報,那就是投資高風險的股票。不容懷疑,這個模型在現代金融理論里占據著主導地位,但是這個模型真的實用麽?
在CAPM里,最難以計算的就是Beta的值。當法瑪(Eugene Fama)和肯尼斯·弗蘭奇(Kenneth French) 研究1963年到1990年期間紐約證交所,美國證交所,以及納斯達克市場(NASDAQ)里的股票回報時發現:在這長時期里Beta值並不能充分解釋股票的表現。單個股票的Beta和回報率之間的線性關係在短時間內也不存在。他們的發現似乎表明瞭CAPM並不能有效地運用於現實的股票市場內!
事實上,有很多研究也表示對CAPM正確性的質疑,但是這個模型在投資界仍然被廣泛的利用。雖然用Beta預測單個股票的變動是困難,但是投資者仍然相信Beta值比較大的股票組合會比市場價格波動性大,不論市場價格是上升還是下降;而Beta值較小的股票組合的變化則會比市場的波動小。
對於投資者尤其是基金經理來說,這點是很重要的。因為在市場價格下降的時候,他們可以投資於Beta值較低的股票。而當市場上升的時候,他們則可投資Beta值大於1的股票上。
對於小投資者的我們來說,我們實沒有必要花時間去計算個別股票與大市的Beta值,因為據筆者瞭解,現時有不少財經網站均有附上個別股票的 Beta值,只要讀者細心留意,但定可以發現得到。
1.應用資本資產定價理論探討風險與報酬之模式,亦可發展出有關證券均衡價格的模式,供作市場交易價格之參考。
2.所謂證券的均衡價格即指對投機者而言,股價不存在任何投機獲利的可能,證券均衡價格為投資證券的預期報酬率,等於效率投資組合上無法有效分散的等量風險,如無風險利率為5%,風險溢酬為8%,股票β繫數值為0.8,則依證券市場線所算該股股價應滿足預期報酬率11.4%,即持有證券的均衡預期報酬率為:
E(Ri) = RF + βi[E(Rm) − Rf]
3.實際上,投資人所獲得的報酬率為股票價格上漲(下跌)的資本利得(或損失),加上股票所發放的現金股利或股票股利,即實際報酬率為:
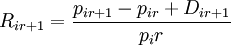
4.在市場均衡時,預期均衡報酬率應等於持有股票的預期報酬率
![R_F+\beta_i[E(R_m)-R_F]=\frac{E(P_{ir+1}-P_{ir}+E(D_{ir+1}))}{P_{ir}}](/w/images/math/e/5/9/e59af741bf0906650166acb2f4bb32ee.png)
5.若股票的市場交易價格低於此均衡價格,投機性買進將有利潤,市場上的超額需求將持續存在直到股價上升至均衡價位;反之若股票的交易價格高於均衡價格,投機者將賣出直到股價下跌達於均衡水準。
- 1.CAPM的假設條件與實際不符:
a.完全市場假設:實際狀況有交易成本,資訊成本及稅,為不完全市場
b.同質性預期假設:實際上投資人的預期非為同質,使SML信息形成一個區間.
c.借貸利率相等,且等於無風險利率之假設:實際情況為借錢利率大於貸款利率。
d.報酬率分配呈常態假設,與事實不一定相符
- 2.CAPM應只適用於資本資產,人力資產不一定可買賣。
- 3.估計的β繫數指代表過去的變動性,但投資人所關心的是該證券未來價格的變動性。
- 4.實際情況中,無風險資產與市場投資組合可能不存在。
- ↑ 吳曉求著.證券投資學.中國人民大學出版社,2009.02.
本条目由以下用户参与贡献
蔓草寒烟,苦行者,Vulture,Angle Roh,村姑,沙漠之鹰,山林,funwmy,Zfj3000,Kane0135,Lolo,Sixdays,Dan,Cabbage,Chenfengxixi,鲈鱼,Steven wyd,Shenp382,风行水使,Yixi,HEHE林,jane409,连晓雾,林巧玲,周翰君,开荒的木头人,Mis铭,刘维燎,151****3899,156****8892.評論(共59條)
謝謝NjuWgl的重新整理
我有一個疑問。CAPM是否能夠有效的評估NPV。通過以上的材料,我們可以發現,CAPM會過分的誇大風險。從而使投資者失去許多賺錢的機會。而且CAPM本身就有很多疑問。但大家都在用它。這到底說明瞭什麼?我有點不太理解。
The model was introduced by Jack Treynor (1961, 1962),[1] William Sharpe (1964), John Lintner (1965a,b) and Jan Mossin (1966) independently, building on the earlier work of Harry Markowitz on diversification and modern portfolio theory.
這是wiki上面的說明,如果只是斷章起義的說是夏普寫的那很不尊重其他有份建立這個模型的大師
真的很不錯,中文就是比英文容易懂啊!
有這個感覺。
這算解析個毛啊,誰能告訴我 β值如何求,計算公式是什麼?
你算什麼東西
這算解析個毛啊,誰能告訴我 β值如何求,計算公式是什麼?
什麼都不懂就吐槽
這算解析個毛啊,誰能告訴我 β值如何求,計算公式是什麼?
1.採用歷史數據,證券收益對市場收益線性回歸,回歸方程的斜率即為所求。 2.根據公式貝塔值為證券收益與市場收益之間協方差與市場組合方差之比。 多看書,少聒噪
為什麼capm 過分誇大風險了
網頁中的latex公式一直顯示不出來,用紅色的大字顯示:解析失敗 (PNG 轉換失敗; 請檢查是否正確安裝了 latex, dvips, gs 和 convert): 然後後面明顯是寫網頁代碼的時候敲進去的公式格式。我在chrome上裝了mathanywhere插件也沒有用,請問該如何解決?









很詳細,很有幫助~