多重賬戶資產組合理論
出自 MBA智库百科(https://wiki.mbalib.com/)
多重賬戶資產組合理論(BPT-MA)
目錄 |
多重賬戶資產組合選擇模型是建立在期望理論之上的。Shefrin和Statman(2000)提出投資者具有兩個心理賬戶,分別對應高、低兩個期望值,代表投資者既想避免貧困,又希望變得富有的願望。高、低期望值兼而有之的資產組合常常被描述為分層的金字塔,投資者在底層和頂層之間分配財富,底層的財富是為了避免貧困,頂層的財富是為了變得富有。投資者的目標就是將現有財富W0在兩個賬戶間分配以使整體效用達到最大。
假設低期望帳戶的效用函數為Cobb-Douglas函數:
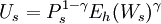
Eh(Ws)γ ,其中Ps代表達不到低期望水平As的概率,Ws代表財富,而γ是一個非負權重參數。類似的,高期望賬戶的效用函數為:
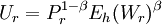
其中各參數含義與前式對應。則可假定投資者的效用函數是低期望賬戶的效用函數與高期望賬戶的效用函數的聯合體為:
![U=(1+K_{dr}[P_r^{1-\beta}E_h(W_r)^\beta])K_{ds}[P_s^{1-\gamma}E_h(W_s)^\gamma]](/w/images/math/6/4/d/64dc054775148862532919b0c3321949.png)
從投資者效用函數的形式可以看出,當低期望賬戶的效用為0時,投資者的效用也為0;而當高期望賬戶的效用為0時,投資者的效用卻不必為0。這意味著財富中的一部分將首先分配給低期望賬戶。如果賣空被允許,投資者在他的高期望賬戶里可能會持有某些證券的空頭,而在低期望賬戶里相應持有其多頭。原因在於兩種心理賬戶之間缺乏統一性,協方差被忽略了。
總之,投資者將心理賬戶與目標相匹配。兩個心理賬戶不統一,最大化投資者整體效用的做法將會使低期望賬戶中的組合比高期望賬戶中的組合看起來更像無風險債券,而與之相反,高期望賬戶里的組合更像彩票。
BPT與MPT的分析框架是相似的,都是在一定風險下尋求最大收益,在風險與收益平面內構造有效邊界,並根據效用函數判斷最優組合。但二者也存在較大差異,這體現在風險度量與未來收益的確定方面,這種差異主要源於對投資者心理與行為理解的不同。
MPT中的投資者對未來各種不同前景出現的概率以及相應的期望值能夠進行客觀公正的估價,而且因為投資者均是理性人,他們的估值也無差異。其直接結果便是產生一條供所有投資者選擇的有效邊界,這條有效邊界不會因人而異。但BPT中的投資者是正常人,他對未來的估計會受到害怕、希望、期望等感情因素的影響,而且不同的投資者其影響程度有所不同。這種差異體現在對未來收益的期望均值估值上的不同,悲觀者會使之偏低而樂觀者會使之偏高,與此對應的是每位投資者都有屬於自己的有效邊界。
MPT 以預期效用理論為基礎,投資者均是風險厭惡者,對待風險的態度始終不變,其差別隻是厭惡程度不同,以效用函數u-δ2 /d 中的d表達風險容忍程度。而BPT以期望理論為基礎,投資者是損失厭惡者,他們一方面尋求安全保證,另一方面又追求高風險以期望獲取高收益。其投資者對風險的態度是多重度量的,用qs 、qp 、A、δ、γ五個參數來描述。由於假定投資者對待風險態度的不同,因而兩個理論對風險的度量也有所不同。MPT以δ或δ2 度量風險,而BPT以概率Pr{ W≤A }度量風險。







