有限差分法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

有限差分法（Finite Differential Method, FDM）

什麼是有限差分法

　　有限差分法是指用泰勒級數展開式將變數的導數寫成變數，在不同時間或空間點值的差分形式的方法。

有限差分法的基本思想^[1]

　　按時間步長和空間步長將時間和空間區域剖分成若幹網格，用未知函數在網格結(節)點上的值所構成的差分近似代替所用偏微分方程中出現的各階導數，從而把表示變數連續變化關係的偏微分方程離散為有限個代數方程，然後解此線性代數方程組，以求出溶質在各網格結(節)點上不同時刻的濃度。

[編輯]

有限差分法的基本步驟

　　（1）剖分滲流區，確定離散點。將所研究的水動力彌散區域按某種幾何形狀(如矩形、任意多邊形等)剖分成網路系統。

　　（2）建立水動力彌散問題的差分方程組。

　　（3）求解差分方程組。採用各種迭代法，如點逐次超松馳方法(SOR)、線逐次超松馳方法(LSOR)、迭代的交替方向隱式方法(IADI)及強隱式方法(SID)等。

[編輯]

期權定價的有限差分方法^[2]

　　通過求解衍生證券所滿足的微分方程，有限差分法可用來為衍生證券估價，步驟如下：

　　1.將衍生證券的定解區域網格化（區域剖分）

　　對一個不付紅利的衍生證券，其滿足的微分方程為：

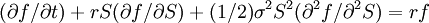$(\partial f/\partial t)+rS(\partial f/\partial S)+(1/2)\sigma^2S^2(\partial^2 f/\partial^2 S)=rf$ 　　(1)

　　現在分別對時間（從0時刻到到期日）和股票價格（ $S m a x$ )為可達到的足夠高的股票價格）進行分割，即\triangle S=S_{max}/M,\triangle T/N,這樣就分別有N+1個時間段和M+1個股票價格，建立如圖(所示的坐標方格，將定解區域網格化，坐標方格上的點（i,j）對應時刻 ${i,j}i\triangle t$ 和股票價格 $j\triangle|S$ ，用變數 $f i, j$ 表示（i,j）點的期權價格。

　　2.建立差分格式

　　（1）內含的有限差分方法

　　其步驟可分為以下幾步：

　　(1)求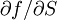 $\partial f/\partial S$ 前向差分近似: $\partial f/\partial S=(f_{i,j+1}-f_{i,j})=\triangle S$ 　　(2)

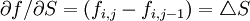　　後向差分格式： $\partial f/\partial S=(f_{i,j}-f_{i,j-1})=\triangle S$ 　　(3)

　　將(2),(3)式平均可更加對稱地求出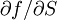 $\partial f/\partial S$ 的近似，即

　　 $\partial f/\partial S=(f_{i,j+1}-f_{i,j-1})/\triangle S$ 　　(4)

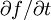　　(2)求 $\partial f/\partial t$ 用前向差分近似：

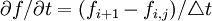　　 $\partial f/\partial t=(f_{i+1}-f_{i,j})/\triangle t$ 　　(5)

　　(3)求 $\partial^2 f/\partial^2 S$

　　 $\partial^2 f/\partial^2 S=[(f_{i,j+1}-f_{i,j})/\triangle S-(f_{i,j}-f_{i,j-1})/\triangle S]/\triangle S=(f_{i,j-1}+f_{i,j+1}-2f_{i,j})/\triangle S$ 　　(6)

　　(4)將(4),(5),(6)式代入(1)式可得到內含有限差分公式：

　　 $a j f i, j - 1 + b j f i, j - c j f i, j + 1 = f i + 1, j$ 　　(7)

　　其中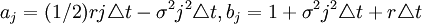： $a_j=(1/2)rj\triangle t-\sigma^2j^2\triangle t,b_j=1+\sigma^2j^2\triangle t+r\triangle t$

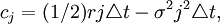　　 $c_j=(1/2)rj\triangle t-\sigma^2j^2\triangle t,$ i=0,1,…，N-1。j=0,1…，M-1

　　針對看跌期權和看漲期權可分別求出方程的邊界條件：

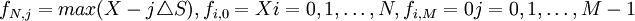
　　看跌期權： $f_{N,j}=max(X-j\triangle S),f_{i,0}=X i=0,1,\ldots,N,f_{i,M}=0 j=0,1,\ldots,M-1$

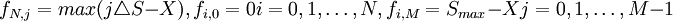
　　看漲期權： $f_{N,j}=max(j\triangle S-X),f_{i,0}=0 i=0,1,\ldots,N,f_{i,M}=S_{max}-X j=0,1,\ldots,M-1$

　　(5)利用邊界條件和(7)式可以給出M-1個聯立方程組：

　　 $a j f N - 1, j - 1 + b j f N - 1, j + c j f N - 1, j + 1$ 　j=1,2…，M-1

　　求解這M-1個聯立方程組即可以求出期權價格，但對美式看跌期權時我們必須考慮其提前執行的情況。

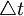　　內含有限差分法的優點是它很有效，當 $\triangle S$ 和 $\triangle t$ 都趨於0時，它總是收斂於微分方程組的解，即收斂性較好，但缺點是必須求解M-1個聯立方程，計算較複雜。

　　2.外推的有限差分方法

　　外推的有限差分方法可以剋服內含有限差分法的缺點，但是其假設條件是在股票價格相同時，i時刻與i+1時刻的f對S的一階、二階偏導數相同，因此(4),(5),(6)式分別變為：

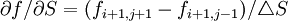　　 $\partial f/\partial S=(f_{i+1,j+1}-f_{i+1,j-1})/\triangle S$ 　　(8)

　　 $f/\partial^2 t=(f_{i+1,j}-f_{i,j})/\triangle S$ 　　(9)

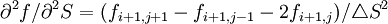　　 $\partial^2 f/\partial^2 S=(f_{i+1,j+1}-f_{i+1,j-1}-2f_{i+1,j})/\triangle S^2$ 　　(10)

　　將(8),(9),(10)分別代入(1)可得到外推有限差分方程：

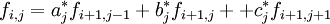　　 $f_{i,j}=a^*_jf_{i+1,j-1}+b_j^*f_{i+1,j}++c_j^*f_{i+1,j+1}$ 　　 $(7) *$

　　 $a^*_j=[1/(\triangle t)][-1/(\triangle t)+(1/2)\partial^2j^2\triangle t]$

　　 $b^*_j=[1/(1+r\triangle t)][1-\partial^2j^2\triangle t]$

　　 $c^*_j=[1/(\triangle t)][1/2(\triangle t)+(1/2)\partial^2j^2\triangle t]$

　　外推的有限差分方法可更好地用於計算期權價值，但收斂性更差。

　　3.其他有限差分法

　　一是Hopscotch法，即交叉使用內含和外推法計算節點的期權價值，也稱“跳格子法”。二是Grank-Nicholson法，求內含和外推法的平均值，即將(7)和 $(7) *$ 平均求得期權價值。使用有限差分法有時可置換變數，如令Z=ln S而不以S為標的變數，使計算更有效。

[編輯]

有限差分法與期權定價模型的聯繫

　　1.與Black-Scholes定價模型的聯繫

　　用模型得到的是精確解，而用有限差分法得到的是近似解，但兩種方法的計算結果是接近的。

　　2.與樹圖法的聯繫

　　它們的計算都是從衍生證券有效期的最後時刻倒推到開始時刻，都能適合美式和歐式期權的定價，但當最終盈虧狀態依賴於變數的過去歷史和當前值時，應用它們就存在困難。外推有限差分法與樹圖法很相似，

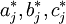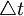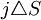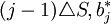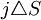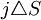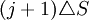　　其中 $a^*_j,b^*_j,c^*_j$ 可解釋為 $\triangle t$ 時間間隔內股票價格變化概率 $a^*_j$ 是從 $j\triangle S$ 降到 $(j-1)\triangle S,b^*_j$ 是保持在 $j\triangle S$ 不變， $c^*_j$ 是從 $j\triangle S$ 升到 $(j+1)\triangle S$ 概率。