遠期利率
出自 MBA智库百科(https://wiki.mbalib.com/)
遠期利率(Forward Rate)
目錄 |
遠期利率則是指隱含在給定的即期利率之中,從未來的某一時點到另一時點的利率。
如果我們已經確定了收益率曲線,那麼所有的遠期利率就可以根據收益率曲線上的即期利率求得。所以遠期利率並不是一組獨立的利率, 而是和收益率曲線緊密相連的。在成熟市場中, 一些遠期利率也可以直接從市場上觀察到, 即根據利率遠期或期貨合約的市場價格推算出來。
遠期利率的種類[1]
1×2遠期利率,即表示1個月之後開始的期限1個月的遠期利率;2×4遠期利率,則表示2個月之後開始的期限為2個月的遠期利率。
遠期利率的決定[1]
遠期利率是由一系列即期利率決定的。
假設現在時刻為 t,T 時刻到期的即期利率為 r,T * 時刻(T * > T)到期的即期利率為r * ,則t時刻的T * − T期間的遠期利率rF應滿足以下等式:
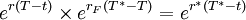
rF(T * − T) = r * (T * − t) − r(T − t) (1)
若式(1)不成立,就存在套利空間。
對rF(T * − T) = r * (T * − t) − r(T − t)變形可得:
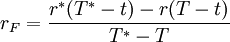 (2)
(2)
這是遠期利率的常用計算公式,進一步變形可得
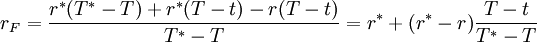 (3)
(3)
如果即期利率期限結構在T * − T期間是向上傾斜的,即r * > r,則rF > r * ;
如果即期利率期限結構在T^*-T期間是向下傾斜的,即r * < r,則rF < r * 。
遠期利率的公式 [2]
如以ft − 1,t 代表第 t-1年至第t年間的遠期利率,St代表t年期即期利率,St − 1代表t-1年期即期利率,其一般計算式是:
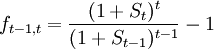 (4)
(4)
舉例說明:
已知2年期的即期利率為5%,3年期即期利率為6%,求第2年至第3年的遠期利率是多少?
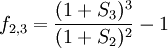 (5)
(5)
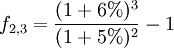 (6)
(6)
f2,3 = 8% (7)
遠期利率的重要性 [2]
在現代金融分析中,遠期利率有著非常廣泛的應用。它們可以預示市場對未來利率走勢的期望,一直是中央銀行制定和執行貨幣政策的參考工具。更重要的是, 在成熟市場中幾乎所有利率衍生品的定價都依賴於遠期利率。雖然我國目前還沒有利率衍生品, 但隨著金融全球化的發展,我國對外開放的進一步擴大和利率市場化改革的全面推進,引進這些金融工具是勢在必行的。我們將舉例說明不同的方法雖然能夠構造相近的收益率曲線或即期利率曲線,但它們所給出的遠期利率卻會有很大的不同, 從而造成利率衍生品定價的明顯不同。因此我們有必要在構造收益率曲線的時候, 考察相應的遠期利率。
為什麼不同的方法能夠給出相近的即期利率但相應的遠期利率卻有可能相差很大呢?我們可以通過下麵一個簡單的例子來理解這個現象。設Si, i = 1,2,3..., 是期限為i年的即期利率, 而fj, j = 0,1,2..., 是第j年開始期限為一年的遠期利率。一般對於T年的即期利率,我們有如下關係:
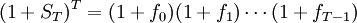 (8)
(8)
假如ST發生一個變化δST , 如果我們保持其它遠期利率不變, 而只有fT − 1可變, 那麼ST的變化對fT − 1有多大的影響呢? 考慮到一般我們有ST<<1和fT − 1<<1, 對(8)式兩邊求微分我們便近似地得到:
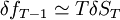 (9)
(9)
這說明瞭在T很大的時候, 即期利率很小的變化也可能帶來遠期利率的較大變化。一般來說,一個T年的即期利率的變化所引起的累積影響較大, 而一年期的遠期利率只對一年的利息產生影響, 所以一年期的遠期利率必需作很大的調整才能使T年內所產生的總的影響和即期利率一樣。這就是不同的方法所得到的即期利率的差別即便很小, 它們所給出的遠期利率的差別卻有可能很大的原因。
遠期利率和即期利率的區別[2]
即期利率和遠期利率的區別在於計息日起點不同,即期利率的起點在當前時刻,而遠期利率的起點在未來某一時刻。
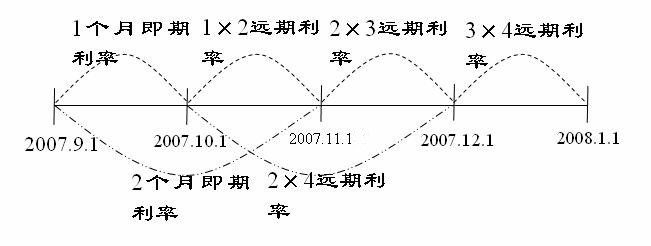








補充了遠期利率的決定和種類