博弈論
出自 MBA智库百科(https://wiki.mbalib.com/)
- 該條目對應的頁面分類是博弈論。
博弈論(Game Theory),也稱對策論或競賽論
目錄 |
博弈論(Game Theory),博弈論是指研究多個個體或團隊之間在特定條件制約下的對局中利用相關方的策略,而實施對應策略的學科。有時也稱為對策論,或者賽局理論,是研究具有鬥爭或競爭性質現象的理論和方法,它是應用數學的一個分支,既是現代數學的一個新分支,也是運籌學的一個重要學科。目前在生物學、經濟學、國際關係學、電腦科學、政治學、軍事戰略和其他很多學科都有廣泛的應用。主要研究公式化了的激勵結構(游戲或者博弈(Game))間的相互作用.
博弈論考慮博弈中的個體的預測行為和實際行為,並研究它們的優化策略。錶面上不同的相互作用可能表現出相似的激勵結構(incentive structure),所以他們是同一個游戲的特例。其中一個有名有趣的應用例子是囚徒困境悖論(Prisoner's dilemma)。
具有競爭或對抗性質的行為成為博弈行為。在這類行為中,參加鬥爭或競爭的各方各自具有不同的目標或利益。為了達到各自的目標和利益,各方必須考慮對手的各種可能的行動方案,並力圖選取對自己最為有利或最為合理的方案。比如日常生活中的下棋,打牌等。博弈論就是研究博弈行為中鬥爭各方是否存在著最合理的行為方案,以及如何找到這個合理的行為方案的數學理論和方法。
生物學家使用博弈理論來理解和預測進化論的某些結果。例如:John Maynard Smith 和George R. Price在1973年發表於Nature上的論文中提出的“evolutionarily stable strategy”的這個概念就是使用了博弈理論。還可以參見演化博弈理論(evolutionary game theory)和行為生態學(behavioral ecology)。
博弈論思想古已有之,我國古代的《孫子兵法》就不僅是一部軍事著作,而且算是最早的一部博弈論專著。博弈論最初主要研究象棋、橋牌、賭博中的勝負問題,人們對博弈局勢的把握只停留在經驗上,沒有向理論化發展,正式發展成一門學科則是在20世紀初。
對於博弈論的研究,開始於策墨洛(Zermelo,1913)、波雷爾(Borel,1921)及馮·諾伊曼(von Neumann, 1928),後來由馮·諾伊曼和奧斯卡·摩根斯坦(von Neumann and Morgenstern,1944,1947)首次對其系統化和形式化(參照Myerson, 1991)。隨後約翰·福布斯·納什(John Forbes Nash Jr., 1950, 1951)利用不動點定理證明瞭均衡點的存在,為博弈論的一般化奠定了堅實的基礎。此外,塞爾頓、哈桑尼的研究也對博弈論發展起到推動作用。今天博弈論已發展成一門較完善的的學科。
通常認為,現代經濟博弈論是在20世紀50年代由匈牙利/美國著名數學家馮·諾依曼(von Neumann)的經濟學家奧斯卡·摩根斯坦(Oscar Morgenstern)引入經濟學的,目前已成為經濟分析的主要工具之一,對產業組織理論、委托代理理論、信息經濟學等經濟理論的發展做出了非常重要的貢獻。1994年的諾貝爾經濟學獎頒發給了約翰·納什(John Nash)等三位在博弈論研究中成績卓著的經濟學家,1996年的諾貝爾經濟學獎又授予在博弈論的應用方面有著重大成就的經濟學家。由於博弈論重視經濟主體之間的相互聯繫及其辨證關係,大大拓寬了傳統經濟學的分析思路,使其更加接近現實市場競爭,從而成為現代微觀經濟學的重要基石,也為現代巨集觀經濟學提供了更加堅實的微觀基礎。
當代博弈論的“三大家”和“四君子”
"三大家" 包括約翰·福布斯·納什、約翰·C·海薩尼以及萊因哈德·澤爾騰。這三人同時因為他們對博弈論的突出貢獻而獲得1994年的瑞典銀行經濟學獎(也稱諾貝爾經濟學獎)。
"四君子" 包括羅伯特·J·奧曼、肯·賓摩爾、戴維·克瑞普斯以及阿裡爾·魯賓斯坦。
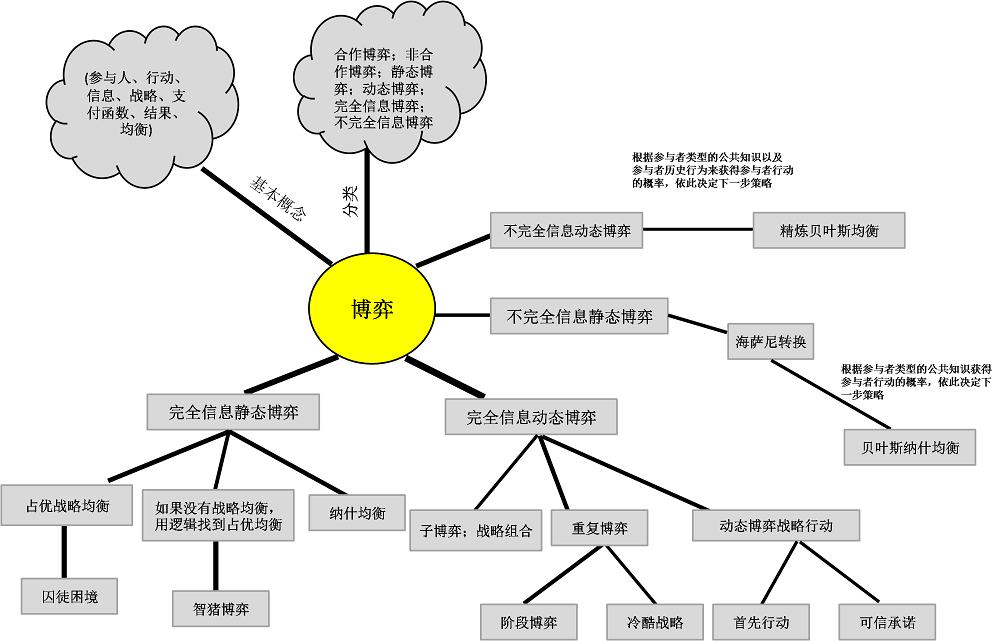
博弈要素:
(1)局中人(players):在一場競賽或博弈中,每一個有決策權的參與者成為一個局中人。只有兩個局中人的博弈現象稱為“兩人博弈”,而多於兩個局中人的博弈稱為 “多人博弈”。
(2)策略(strategies):一局博弈中,每個局中人都有選擇實際可行的完整的行動方案,即方案不是某階段的行動方案,而是指導整個行動的一個方案,一個局中人的一個可行的自始至終全局籌劃的一個行動方案,稱為這個局中人的一個策略。如果在一個博弈中局中人都總共有有限個策略,則稱為“有限博弈”,否則稱為“無限博弈”。
(3)得失(payoffs):一局博弈結局時的結果稱為得失。每個局中人在一局博弈結束時的得失,不僅與該局中人自身所選擇的策略有關,而且與全局中人所取定的一組策略有關。所以,一局博弈結束時每個局中人的“得失”是全體局中人所取定的一組策略的函數,通常稱為支付(payoff)函數。
(4)次序(orders):各博弈方的決策有先後之分,且一個博弈方要作不止一次的決策選擇,就出現了次序問題;其他要素相同次序不同,博弈就不同。
(5)博弈涉及到均衡:均衡是平衡的意思,在經濟學中,均衡意即相關量處於穩定值。在供求關係中,某一商品市場如果在某一價格下,想以此價格買此商品的人均能買到,而想賣的人均能賣出,此時我們就說,該商品的供求達到了均衡。所謂納什均衡,它是一穩定的博弈結果。
納什均衡(Nash Equilibrium):在一策略組合中,所有的參與者面臨這樣一種情況,當其他人不改變策略時,他此時的策略是最好的。也就是說,此時如果他改變策略他的支付將會降低。在納什均衡點上,每一個理性的參與者都不會有單獨改變策略的衝動。納什均衡點存在性證明的前提是“博弈均衡偶”概念的提出。所謂“均衡偶”是在二人零和博弈中,當局中人A採取其最優策略a*,局中人B也採取其最優策略b*,如果局中人B仍採取b*,而局中人A卻採取另一種策略a,那麼局中人A的支付不會超過他採取原來的策略a*的支付。這一結果對局中人B亦是如此。
這樣,“均衡偶”的明確定義為:一對策略a*(屬於策略集A)和策略b*(屬於策略集B)稱之為均衡偶,對任一策略a(屬於策略集A)和策略b(屬於策略集B),總有:偶對(a, b*)≤偶對(a*,b*)≥偶對(a*,b)。
對於非零和博弈也有如下定義:一對策略a*(屬於策略集A)和策略b*(屬於策略集B)稱為非零和博弈的均衡偶,對任一策略a(屬於策略集A)和策略 b(屬於策略集B),總有:對局中人A的偶對(a, b*) ≤偶對(a*,b*);對局中人B的偶對(a*,b)≤偶對(a*,b*)。
有了上述定義,就立即得到納什定理:
任何具有有限純策略的二人博弈至少有一個均衡偶。這一均衡偶就稱為納什均衡點。
納什定理的嚴格證明要用到不動點理論,不動點理論是經濟均衡研究的主要工具。通俗地說,尋找均衡點的存在性等價於找到博弈的不動點。
納什均衡點概念提供了一種非常重要的分析手段,使博弈論研究可以在一個博弈結構里尋找比較有意義的結果。
但納什均衡點定義只局限於任何局中人不想單方面變換策略,而忽視了其他局中人改變策略的可能性,因此,在很多情況下,納什均衡點的結論缺乏說服力,研究者們形象地稱之為“天真可愛的納什均衡點”。
塞爾頓(R·Selten)在多個均衡中剔除一些按照一定規則不合理的均衡點,從而形成了兩個均衡的精煉概念:子博弈完全均衡和顫抖的手完美均衡。
合作博弈和非合作博弈的區別在於相互發生作用的當事人之間有沒有一個具有約束力的協議,如果有,就是合作博弈,如果沒有,就是非合作博弈。
靜態博弈是指在博弈中,參與人同時選擇或雖非同時選擇但後行動者並不知道先行動者採取了什麼具體行動;
動態博弈是指在博弈中,參與人的行動有先後順序,且後行動者能夠觀察到先行動者所選擇的行動。通俗的理解:"囚徒困境"就是同時決策的,屬於靜態博弈;而棋牌類游戲等決策或行動有先後次序的,屬於動態博弈
完全博弈是指在博弈過程中,每一位參與人對其他參與人的特征、策略空間及收益函數有準確的信息。
不完全信息博弈是指如果參與人對其他參與人的特征、策略空間及收益函數信息瞭解的不夠準確、或者不是對所有參與人的特征、策略空間及收益函數都有準確的信息,在這種情況下進行的博弈就是不完全信息博弈。
目前經濟學家們現在所談的博弈論一般是指非合作博弈,由於合作博弈論比非合作博弈論複雜,在理論上的成熟度遠遠不如非合作博弈論。非合作博弈又分為:完全信息靜態博弈,完全信息動態博弈,不完全信息靜態博弈,不完全信息動態博弈。與上述四種博弈相對應的均衡概念為:納什均衡(Nash equilibrium),子博弈精煉納什均衡(subgame perfect Nash equilibrium),貝葉斯納什均衡(Bayesian Nash equilibrium),精煉貝葉斯納什均衡(perfect Bayesian Nash equilibrium)。
博弈論還有很多分類,比如:以博弈進行的次數或者持續長短可以分為有限博弈和無限博弈;以表現形式也可以分為一般型(戰略型)或者展開型,等等。
博弈論的研究方法和其他許多利用數學工具研究社會經濟現象的學科一樣,都是從複雜的現象中抽象出基本的元素,對這些元素構成的數學模型進行分析,而後逐步引入對其形勢產生影響的其他因素,從而分析其結果。
基於不同抽象水平,形成三種博弈表述方式,標準型、擴展型和特征函數型,利用這三種表述形式,可以研究形形色色的問題。因此,它被稱為“社會科學的數學”從理論上講,博弈論是研究理性的行動者相互作用的形式理論,而實際上正深入到經濟學、政治學、社會學等等,被各門社會科學所應用。
博弈論是指某個個人或是組織,面對一定的環境條件,在一定的規則約束下,依靠所掌握的信息,從各自選擇的行為或是策略進行選擇並加以實施,並從各自取得相應結果或收益的過程,在經濟學上博弈論是個非常重要的理論概念。
什麼是博弈論?古語有雲,世事如棋。生活中每個人如同棋手,其每一個行為如同在一張看不見的棋盤上布一個子,精明慎重的棋手們相互揣摩、相互牽制,人人爭贏,下出諸多精彩紛呈、變化多端的棋局。博弈論是研究棋手們 “出棋” 著數中理性化、邏輯化的部分,並將其系統化為一門科學。換句話說,就是研究個體如何在錯綜複雜的相互影響中得出最合理的策略。事實上,博弈論正是衍生於古老的游戲或曰博弈如象棋、撲克等。數學家們將具體的問題抽象化,通過建立自完備的邏輯框架、體系研究其規律及變化。這可不是件容易的事情,以最簡單的二人對弈為例,稍想一下便知此中大有玄妙:若假設雙方都精確地記得自己和對手的每一步棋且都是最“理性” 的棋手,甲出子的時候,為了贏棋,得仔細考慮乙的想法,而乙出子時也得考慮甲的想法,所以甲還得想到乙在想他的想法,乙當然也知道甲想到了他在想甲的想法…
面對如許重重迷霧,博弈論怎樣著手分析解決問題,怎樣對作為現實歸納的抽象數學問題求出最優解、從而為在理論上指導實踐提供可能性呢?現代博弈理論由匈牙利大數學家馮·諾伊曼於20世紀20年代開始創立,1944年他與經濟學家奧斯卡·摩根斯特恩合作出版的巨著《博弈論與經濟行為》,標志著現代系統博弈理論的初步形成。對於非合作、純競爭型博弈,諾伊曼所解決的只有二人零和博弈--好比兩個人下棋、或是打乒乓球,一個人贏一著則另一個人必輸一著,凈獲利為零。在這裡抽象化後的博弈問題是,已知參與者集合(兩方) ,策略集合(所有棋著) ,和盈利集合(贏子輸子) ,能否且如何找到一個理論上的“解” 或“平衡” ,也就是對參與雙方來說都最“合理” 、最優的具體策略?怎樣才是“合理” ?應用傳統決定論中的“最小最大” 準則,即博弈的每一方都假設對方的所有功略的根本目的是使自己最大程度地失利,並據此最優化自己的對策,諾伊曼從數學上證明,通過一定的線性運算,對於每一個二人零和博弈,都能夠找到一個“最小最大解” 。通過一定的線性運算,競爭雙方以概率分佈的形式隨機使用某套最優策略中的各個步驟,就可以最終達到彼此盈利最大且相當。當然,其隱含的意義在於,這套最優策略並不依賴於對手在博弈中的操作。用通俗的話說,這個著名的最小最大定理所體現的基本“理性” 思想是“抱最好的希望,做最壞的打算” 。
- 一、經濟學中的“智豬博弈”(Pigs’payoffs)
這個例子講的是:豬圈裡有兩頭豬,一頭大豬,一頭小豬。豬圈的一邊有個踏板,每踩一下踏板,在遠離踏板的豬圈的另一邊的投食口就會落下少量的食物。如果有一隻豬去踩踏板,另一隻豬就有機會搶先吃到另一邊落下的食物。當小豬踩動踏板時,大豬會在小豬跑到食槽之前剛好吃光所有的食物;若是大豬踩動了踏板,則還有機會在小豬吃完落下的食物之前跑到食槽,爭吃到另一半殘羹。
那麼,兩隻豬各會採取什麼策略?答案是:小豬將選擇“搭便車”策略,也就是舒舒服服地等在食槽邊;而大豬則為一點殘羹不知疲倦地奔忙於踏板和食槽之間。
原因何在?因為,小豬踩踏板將一無所獲,不踩踏板反而能吃上食物。對小豬而言,無論大豬是否踩動踏板,不踩踏板總是好的選擇。反觀大豬,已明知小豬是不會去踩動踏板的,自己親自去踩踏板總比不踩強吧,所以只好親力親為了。
“小豬躺著大豬跑”的現象是由於故事中的游戲規則所導致的。規則的核心指標是:每次落下的食物數量和踏板與投食口之間的距離。
如果改變一下核心指標,豬圈裡還會出現同樣的“小豬躺著大豬跑”的景象嗎?試試看。
改變方案一:減量方案。投食僅原來的一半分量。結果是小豬大豬都不去踩踏板了。小豬去踩,大豬將會把食物吃完;大豬去踩,小豬將也會把食物吃完。誰去踩踏板,就意味著為對方貢獻食物,所以誰也不會有踩踏板的動力了。
如果目的是想讓豬們去多踩踏板,這個游戲規則的設計顯然是失敗的。
改變方案二:增量方案。投食為原來的一倍分量。結果是小豬、大豬都會去踩踏板。誰想吃,誰就會去踩踏板。反正對方不會一次把食物吃完。小豬和大豬相當於生活在物質相對豐富的“共產主義”社會,所以競爭意識卻不會很強。
對於游戲規則的設計者來說,這個規則的成本相當高(每次提供雙份的食物);而且因為競爭不強烈,想讓豬們去多踩踏板的效果並不好。
改變方案三:減量加移位方案。投食僅原來的一半分量,但同時將投食口移到踏板附近。結果呢,小豬和大豬都在拼命地搶著踩踏板。等待者不得食,而多勞者多得。每次的收穫剛好消費完。
對於游戲設計者,這是一個最好的方案。成本不高,但收穫最大。
原版的“智豬博弈”故事給了競爭中的弱者(小豬)以等待為最佳策略的啟發。但是對於社會而言,因為小豬未能參與競爭,小豬搭便車時的社會資源配置的並不是最佳狀態。為使資源最有效配置,規則的設計者是不願看見有人搭便車的,政府如此,公司的老闆也是如此。而能否完全杜絕“搭便車”現象,就要看游戲規則的核心指標設置是否合適了。
比如,公司的激勵制度設計,獎勵力度太大,又是持股,又是期權,公司職員個個都成了百萬富翁,成本高不說,員工的積極性並不一定很高。這相當於“智豬博弈”增量方案所描述的情形。但是如果獎勵力度不大,而且見者有份(不勞動的“小豬”也有),一度十分努力的大豬也不會有動力了----就象“智豬博弈”減量方案一所描述的情形。最好的激勵機制設計就象改變方案三----減量加移位的辦法,獎勵並非人人有份,而是直接針對個人(如業務按比例提成),既節約了成本(對公司而言),又消除了“搭便車”現象,能實現有效的激勵。
許多人並未讀過“智豬博弈”的故事,但是卻在自覺地使用小豬的策略。股市上等待莊家抬轎的散戶;等待產業市場中出現具有贏利能力新產品、繼而大舉仿製牟取暴利的游資;公司里不創造效益但分享成果的人,等等。因此,對於制訂各種經濟管理的游戲規則的人,必須深諳“智豬博弈”指標改變的個中道理。
- 二、囚徒困境博弈
在博弈論中,含有占優戰略均衡的一個著名例子是由塔克給出的“囚徒困境”(prisoners’ dilemma)博弈模型。該模型用一種特別的方式為我們講述了一個警察與小偷的故事。假設有兩個小偷A和B聯合犯事、私入民宅被警察抓住。警方將兩人分別置於不同的兩個房間內進行審訊,對每一個犯罪嫌疑人,警方給出的政策是:如果一個犯罪嫌疑人坦白了罪行,交出了贓物,於是證據確鑿,兩人都被判有罪。如果另一個犯罪嫌疑人也作了坦白,則兩人各被判刑8年;如果另一個犯罪嫌疑人沒有坦白而是抵賴,則以妨礙公務罪(因已有證據表明其有罪)再加刑2年,而坦白者有功被減刑8年,立即釋放。如果兩人都抵賴,則警方因證據不足不能判兩人的偷竊罪,但可以私入民宅的罪名將兩人各判入獄1年。下表給出了這個博弈的支付矩陣。
表 囚徒困境博弈 [Prisoner's dilemma]
B 坦白 B 抵賴 A 坦白 –8, –8 0, –10 A 抵賴 –10, 0 –1, –1
我們來看看這個博弈可預測的均衡是什麼。對A來說,儘管他不知道B作何選擇,但他知道無論B選擇什麼,他選擇“坦白”總是最優的。顯然,根據對稱性,B也會選擇“坦白”,結果是兩人都被判刑8年。但是,倘若他們都選擇“抵賴”,每人只被判刑1年。在表2.2中的四種行動選擇組合中,(抵賴、抵賴)是帕累托最優的,因為偏離這個行動選擇組合的任何其他行動選擇組合都至少會使一個人的境況變差。不難看出,“坦白”是任一犯罪嫌疑人的占優戰略,而(坦白,坦白)是一個占優戰略均衡。
要瞭解納什的貢獻,首先要知道什麼是非合作博弈問題。現在幾乎所有的博弈論教科書上都會講“囚犯的兩難處境”的例子,每本書上的例子都大同小異。
博弈論畢竟是數學,更確切地說是運籌學的一個分支,談經論道自然少不了數學語言,外行人看來只是一大堆數學公式。好在博弈論關心的是日常經濟生活問題,所以不能不食人間煙火。其實這一理論是從棋弈、撲克和戰爭等帶有競賽、對抗和決策性質的問題中借用的術語,聽上去有點玄奧,實際上卻具有重要現實意義。博弈論大師看經濟社會問題猶如棋局,常常寓深刻道理於游戲之中。所以,多從我們的日常生活中的凡人小事入手,以我們身邊的故事做例子,娓娓道來,並不乏味。
話說有一天,一位富翁在家中被殺,財物被盜。警方在此案的偵破過程中,抓到兩個犯罪嫌疑人,斯卡爾菲絲和那庫爾斯,並從他們的住處搜出被害人家中丟失的財物。但是,他們矢口否認曾殺過人,辯稱是先發現富翁被殺,然後只是順手牽羊偷了點兒東西。於是警方將兩人隔離,分別關在不同的房間進行審訊。由地方檢察官分別和每個人單獨談話。
檢察官說,“由於你們的偷盜罪已有確鑿的證據,所以可以判你們一年刑期。但是,我可以和你做個交易。如果你單獨坦白殺人的罪行,我只判你三個月的監禁,但你的同伙要被判十年刑。如果你拒不坦白,而被同伙檢舉,那麼你就將被判十年刑,他只判三個月的監禁。但是,如果你們兩人都坦白交代,那麼,你們都要被判5年刑。”斯卡爾菲絲和那庫爾斯該怎麼辦呢?他們面臨著兩難的選擇——坦白或抵賴。顯然最好的策略是雙方都抵賴,結果是大家都只被判一年。但是由於兩人處於隔離的情況下無法串供。所以,按照亞當·斯密的理論,每一個人都是從利己的目的出發,他們選擇坦白交代是最佳策略。因為坦白交代可以期望得到很短的監禁———3個月,但前提是同伙抵賴,顯然要比自己抵賴要坐10年牢好。這種策略是損人利己的策略。不僅如此,坦白還有更多的好處。如果對方坦白了而自己抵賴了,那自己就得坐10年牢。太不划算了!因此,在這種情況下還是應該選擇坦白交代,即使兩人同時坦白,至多也只判5年,總比被判 10年好吧。所以,兩人合理的選擇是坦白,原本對雙方都有利的策略(抵賴)和結局(被判1年刑)就不會出現。
這樣兩人都選擇坦白的策略以及因此被判5年的結局被稱為“納什均衡”,也叫非合作均衡。因為,每一方在選擇策略時都沒有“共謀”(串供),他們只是選擇對自己最有利的策略,而不考慮社會福利或任何其他對手的利益。也就是說,這種策略組合由所有局中人(也稱當事人、參與者)的最佳策略組合構成。沒有人會主動改變自己的策略以便使自己獲得更大利益。“囚徒的兩難選擇”有著廣泛而深刻的意義。個人理性與集體理性的衝突,各人追求利己行為而導致的最終結局是一個“納什均衡”,也是對所有人都不利的結局。他們兩人都是在坦白與抵賴策略上首先想到自己,這樣他們必然要服長的刑期。只有當他們都首先替對方著想時,或者相互合謀(串供)時,才可以得到最短時間的監禁的結果。“納什均衡”首先對亞當·斯密的“看不見的手”的原理提出挑戰。按照斯密的理論,在市場經濟中,每一個人都從利己的目的出發,而最終全社會達到利他的效果。
不妨讓我們重溫一下這位經濟學聖人在《國富論》中的名言:“通過追求(個人的)自身利益,他常常會比其實際上想做的那樣更有效地促進社會利益。”從“納什均衡”我們引出了“看不見的手”的原理的一個悖論:從利己目的出發,結果損人不利己,既不利己也不利他。兩個囚徒的命運就是如此。從這個意義上說,“納什均衡”提出的悖論實際上動搖了西方經濟學的基石。因此,從“納什均衡”中我們還可以悟出一條真理:合作是有利的“利己策略”。但它必須符合以下黃金律:按照你願意別人對你的方式來對別人,但只有他們也按同樣方式行事才行。也就是中國人說的“己所不欲勿施於人”。但前提是人所不欲勿施於我。其次,“納什均衡”是一種非合作博弈均衡,在現實中非合作的情況要比合作情況普遍。所以“納什均衡”是對馮·諾依曼和摩根斯特恩的合作博弈理論的重大發展,甚至可以說是一場革命。
從“納什均衡”的普遍意義中我們可以深刻領悟司空見慣的經濟、社會、政治、國防、管理和日常生活中的博弈現象。我們將例舉出許多類似於“囚徒的兩難處境” 這樣的例子。如價格戰博弈、軍奮競賽博弈、污染博弈等等。一般的博弈問題由三個要素所構成:即局中人(players)又稱當事人、參與者、策略等等的集合,策略 (strategies)集合以及每一對局中人所做的選擇和贏得(payoffs)集合。其中所謂贏得是指如果一個特定的策略關係被選擇,每一局中人所得到的效用。所有的博弈問題都會遇到這三個要素。
- 三、價格戰博弈
現在我們經常會遇到各種各樣的家電價格大戰,彩電大戰、冰箱大戰、空調大戰、微波爐大戰……這些大戰的受益者首先是消費者。每當看到一種家電產品的價格大戰,百姓都會“沒事兒偷著樂”。在這裡,我們可以解釋廠家價格大戰的結局也是一個“納什均衡”,而且價格戰的結果是誰都沒錢賺。因為博弈雙方的利潤正好是零。競爭的結果是穩定的,即是一個“納什均衡”。這個結果可能對消費者是有利的,但對廠商而言是災難性的。所以,價格戰對廠商而言意味著自殺。從這個案例中我們可以引伸出兩個問題,一是競爭削價的結果或“納什均衡”可能導致一個有效率的零利潤結局。二是如果不採取價格戰,作為一種敵對博弈論 (vivalry game)其結果會如何呢?每一個企業,都會考慮採取正常價格策略,還是採取高價格策略形成壟斷價格,並儘力獲取壟斷利潤。如果壟斷可以形成,則博弈雙方的共同利潤最大。這種情況就是壟斷經營所做的,通常會抬高價格。另一個極端的情況是廠商用正常的價格,雙方都可以獲得利潤。從這一點,我們又引出一條基本準則:“把你自己的戰略建立在假定對手會按其最佳利益行動的基礎上”。事實上,完全競爭的均衡就是“納什均衡”或“非合作博弈均衡”。在這種狀態下,每一個廠商或消費者都是按照所有的別人已定的價格來進行決策。在這種均衡中,每一企業要使利潤最大化,消費者要使效用最大化,結果導致了零利潤,也就是說價格等於邊際成本。在完全競爭的情況下,非合作行為導致了社會所期望的經濟效率狀態。如果廠商採取合作行動並決定轉向壟斷價格,那麼社會的經濟效率就會遭到破壞。這就是為什麼WTO和各國政府要加強反壟斷的意義所在。
- 四、污染博弈
假如市場經濟中存在著污染,但政府並沒有管制的環境,企業為了追求利潤的最大化,寧願以犧牲環境為代價,也絕不會主動增加環保設備投資。按照看不見的手的原理,所有企業都會從利己的目的出發,採取不顧環境的策略,從而進入“納什均衡”狀態。如果一個企業從利他的目的出發,投資治理污染,而其他企業仍然不顧環境污染,那麼這個企業的生產成本就會增加,價格就要提高,它的產品就沒有競爭力,甚至企業還要破產。這是一個“看不見的手的有效的完全競爭機制”失敗的例證。直到20世紀90年代中期,中國鄉鎮企業的盲目發展造成嚴重污染的情況就是如此。只有在政府加強污染管制時,企業才會採取低污染的策略組合。企業在這種情況下,獲得與高污染同樣的利潤,但環境將更好。
- 五、貿易戰博弈論
這個問題對於剛剛加入WTO的中國而言尤為重要。任何一個國家在國際貿易中都面臨著保持貿易自由與實行貿易保護主義的兩難選擇。貿易自由與壁壘問題,也是一個“納什均衡”,這個均衡是貿易雙方採取不合作博弈的策略,結果使雙方因貿易戰受到損害。X國試圖對Y國進行進口貿易限制,比如提高關稅,則Y國必然會進行反擊,也提高關稅,結果誰也沒有撈到好處。反之,如X和Y能達成合作性均衡,即從互惠互利的原則出發,雙方都減少關稅限制,結果大家都從貿易自由中獲得了最大利益,而且全球貿易的總收益也增加了。
博弈論--這是一個熱得燙手的概念。它不僅僅存在於數學的運籌學中,也正在經濟學中占據越來越重要的地位(近幾年諾貝爾經濟學獎就頻頻授予博弈論研究者),但如果你認為博弈論的應用領域僅限於此的話,那你就大錯了。實際上,博弈論甚至在我們的工作和生活中無處不在!在工作中,你在和上司博弈,也在和下屬博弈,你也同樣會跟其他相關部門人員博弈;而要開展業務,你更是在和你的客戶以及競爭對手博弈。在生活中,博弈仍然無處不在。博弈論代表著一種全新的分析方法和全新的思想。
諾貝爾經濟學獎獲得者包羅·薩繆爾遜如是說:要想在現代社會做個有價值的人,你就必須對博弈論有個大致的瞭解。也可以這樣說,要想贏得生意,不可不學博弈論;要想贏得生活,同樣不可不學博弈論。
博弈論(game theory)對人的基本假定是:人是理性的(rational,或者說自私的),理性的人是指他在具體策略選擇時的目的是使自己的利益最大化,博弈論研究的是理性的人之間如何進行策略選擇的。
納什(John Nash)編製的博弈論經典故事"囚徒的困境",說明瞭非合作博弈及其均衡解的成立,故稱"納什平衡"。
所有的博弈問題都會遇到三個要素。在囚徒的故事中,兩個囚徒是當事人(players)又稱參與者;當事人所做的選擇策略 (strategies)是承認了殺人事實,最後兩個人均贏得(payoffs)了中間的宣判結果。如果兩個囚徒之中有一個承認殺人,另外一個抵賴,不承認殺人,那麼承認者將會得到減刑處理,而抵賴者將會得到最嚴厲的死刑判決,在納什故事中兩個人都承認了犯罪事實,所以兩個囚徒得到的是中間的結果。
類似的: 我們也能從“自私的基因”等理論中看到“納什平衡”的體現。
艾克斯羅德(Robert Axelrod)在開始研究合作之前,設定了兩個前提:一、每個人都是自私的;二、沒有權威干預個人決策。也就是說,個人可以完全按照自己利益最大化的企圖進行決策。在此前提下,合作要研究的問題是:第一、人為什麼要合作;第二、人什麼時候是合作的,什麼時候又是不合作的;第三、如何使別人與你合作。
社會實踐中有很多合作的問題。比如國家之間的關稅報複,對他國產品提高關稅有利於保護本國的經濟,但是國家之間互提關稅,產品價格就提高了,喪失了競爭力,損害了國際貿易的互補優勢。在對策中,由於雙方各自追求自己利益的最大化,導致了群體利益的損害。對策論以著名的囚犯困境來描述這個問題。
A和B各表示一個人,他們的選擇是完全無差異的。選擇C代表合作,選擇D代表不合作。如果AB都選擇C合作,則兩人各得3分;如果一方選C,一方選D,則選C的得零分,選D的得5分;如果AB都選D,雙方各得1分。
顯然,對群體來說最好的結果是雙方都選C,各得3分,共得6分。如果一方選C,一方選D,總體得5分。如果兩人都選D,總體得2分。
對策學界用這個矩陣來描述個體理性與群體理性的衝突:每個人在追求個體利益最大化時,就使群體利益受損,這就是囚徒困境。在矩陣中,對於A來說,當對方選 C,他選D得5分,選C只得3分;當對方選D,他選D得1分,選C得零分。因此,無論對方選C或D,對A來說,選D都得分最多。這是A單方面的優超策略。而當兩個優超策略相遇,即A,B都選D時,結果是各得1分。這個結果在矩陣中並非最優。困境就在於,每個人採取各自的優超策略時,得出的解是穩定的,但不是帕累托最優的,這個結果體現了個體理性與群體理性的矛盾。在數學上,這個一次性決策的矩陣沒有最優解。
如果博弈進行多次,只要對策者知道博弈次數,他們在最後一次肯定採取互相背叛的策略。既然如此,前面的每一次也就沒有合作的必要,因此,在次數已知的多次博弈中,對策者沒有一次會合作。
如果博弈在多人間進行,而且次數未知,對策者就會意識到,當持續地採取合作並達成默契時,對策者就能持續地各得3分,但如果持續地不合作的話,每個人就永遠得1分。這樣,合作的動機就顯現出來。多次對局下,未來的收益應比現在的收益多一個折現率W,W越大,表示未來的收益越重要。在多人對策持續進行下去,且W比較大,即未來充分重要時,最優的策略是與別人採取的策略有關的。假設某人的策略是,第一次合作,以後只要對方不合作一次,他就永不合作。對這種對策者,當然合作下去是上策。假如有的人不管對方採取什麼策略,他總是合作,那麼總是對他採取不合作的策略得分最多。對於總是不合作的人,也只能採取不合作的策略。
艾克斯羅德做了一個實驗,邀請多人來參加游戲,得分規則與前面的矩陣相同,什麼時候結束游戲是未知的。他要求每個參賽者把追求得分最多的策略寫成電腦程式,然後用單迴圈賽的方式將參賽程式兩兩博弈,以找出什麼樣的策略得分最高。
第一輪游戲有14個程式參加,再加上艾克斯羅德自己的一個隨機程式(即以50%的概率選取合作或不合作),運轉了300次。結果得分最高的程式是加拿大學者羅伯布寫的"一報還一報"(tit for tat)。這個程式的特點是,第一次對局採用合作的策略,以後每一步都跟隨對方上一步的策略,你上一次合作,我這一次就合作,你上一次不合作,我這一次就不合作。艾克斯羅德還發現,得分排在前面的程式有三個特點:第一,從不首先背叛,即"善良的";第二,對於對方的背叛行為一定要報複,不能總是合作,即" 可激怒的";第三,不能人家一次背叛,你就沒完沒了的報複,以後人家只要改為合作,你也要合作,即"寬容性"。
為了進一步驗證上述結論,艾氏決定邀請更多的人再做一次游戲,並把第一次的結果公開發表。第二次徵集到了62個程式,加上他自己的隨機程式,又進行了一次競賽。結果,第一名的仍是"一報還一報"。艾氏總結這次游戲的結論是:第一,"一報還一報"仍是最優策略。第二,前面提到的三個特點仍然有效,因為63人中的前15名里,只有第8名的哈靈頓程式是"不善良的",後15名中,只有1個總是合作的是"善良的"。可激怒性和寬容性也得到了證明。此外,好的策略還必須具有的一個特點是"清晰性",能讓對方在三、五步對局內辨識出來,太複雜的對策不見得好。"一報還一報"就有很好的清晰性,讓對方很快發現規律,從而不得不採取合作的態度。
"一報還一報"的策略在靜態的群體中得到了很好的分數,那麼,在一個動態的進化的群體中,這種合作者能否產生、發展、生存下去呢?群體是會向合作的方向進化,還是向不合作的方向進化?如果大家開始都不合作,能否在進化過程中產生合作?為了回答這些疑問,艾氏用生態學的原理來分析合作的進化過程。
假設對策者所組成的策略群體是一代一代進化下去的,進化的規則包括:一,試錯。人們在對待周圍環境時,起初不知道該怎麼做,於是就試試這個,試試那個,哪個結果好就照哪個去做。第二,遺傳。一個人如果合作性好,他的後代的合作基因就多。第三,學習。比賽過程就是對策者相互學習的過程,"一報還一報"的策略好,有的人就願意學。按這樣的思路,艾氏設計了一個實驗,假設63個對策者中,誰在第一輪中的得分高,他在第二輪的群體中所占比例就越高,而且是他的得分的正函數。這樣,群體的結構就會在進化過程中改變,由此可以看出群體是向什麼方向進化的。
實驗結果很有趣。"一報還一報"原來在群體中占1/63,經過1000代的進化,結構穩定下來時,它占了24%。另外,有一些程式在進化過程中消失了。其中有一個值得研究的程式,即原來前15名中唯一的那個"不善良的"哈靈頓程式,它的對策方案是,首先合作,當發現對方一直在合作,它就突然來個不合作,如果對方立刻報複它,它就恢複合作,如果對方仍然合作,它就繼續背叛。這個程式一開始發展很快,但等到除了"一報還一報"之外的其它程式開始消失時,它就開始下降了。因此,以合作繫數來測量,群體是越來越合作的。
進化實驗揭示了一個哲理:一個策略的成功應該以對方的成功為基礎。"一報還一報"在兩個人對策時,得分不可能超過對方,最多打個平手,但它的總分最高。它賴以生存的基礎是很牢固的,因為它讓對方得到了高分。哈靈頓程式就不是這樣,它得到高分時,對方必然得到低分。它的成功是建立在別人失敗的基礎上的,而失敗者總是要被淘汰的,當失敗者被淘汰之後,這個好占別人便宜的成功者也要被淘汰。
那麼,在一個極端自私者所組成的不合作者的群體中,"一報還一報"能否生存呢?艾氏發現,在得分矩陣和未來的折現繫數一定的情況下,可以算出,只要群體的 5%或更多成員是"一報還一報"的,這些合作者就能生存,而且,只要他們的得分超過群體的總平均分,這個合作的群體就會越來越大,最後蔓延到整個群體。反之,無論不合作者在一個合作者占多數的群體中有多大比例,不合作者都是不可能自下而上的。這就說明,社會向合作進化的棘輪是不可逆轉的,群體的合作性越來越大。艾克斯羅德正是以這樣一個鼓舞人心的結論,突破了"囚犯困境"的研究困境。
在研究中發現,合作的必要條件是:第一、關係要持續,一次性的或有限次的博弈中,對策者是沒有合作動機的;第二、對對方的行為要做出回報,一個永遠合作的對策者是不會有人跟他合作的。
那麼,如何提高合作性呢?首先,要建立持久的關係,即使是愛情也需要建立婚姻契約以維持雙方的合作。(火車站的小販為什麼要騙人?為什麼工作中要形成小組制度?換防的時候一方總是要小小地進攻一下的,在中越前線就是這樣)第二、要增強識別對方行動的能力,如果不清楚對方是合作還是不合作,就沒法回報他了。第三、要維持聲譽,說要報複就一定要做到,人家才知道你是不好欺負的,才不敢不與你合作。第四、能夠分步完成的對局不要一次完成,以維持長久關係,比如,貿易、談判都要分步進行,以促使對方採取合作態度。第五、不要嫉妒人家的成功,"一報還一報"正是這樣的典範。第六、不要首先背叛,以免擔上罪魁禍首的道德壓力。第七、不僅對背叛要回報,對合作也要作出回報。第八、不要耍小聰明,占人家便宜。
艾克斯羅德在《合作的進化》一書結尾提出幾個結論。第一、友誼不是合作的必要條件,即使是敵人,只要滿足了關係持續,互相回報的條件,也有可能合作。比如,第一次世界大戰期間,德英兩軍在戰壕戰中遇上了三個月的雨季,雙方在這三個月中達成了默契,互相不攻擊對方的糧車給養,到大反攻時再你死我活地打。這個例子說明,友誼不是合作的前提。第二、預見性也不是合作的前提,艾氏舉出生物界低等動物、植物之間合作的例子來說明這一點。但是,當有預見性的人類瞭解了合作的規律之後,合作進化的過程就會加快。這時,預見性是有用的,學習也是有用的。
當游戲中考慮到隨機干擾,即對策者由於誤會而開始互相背叛的情形時,吳堅忠博士經研究發現,以修正的"一報還一報",即以一定的概率不報複對方的背叛,和 "悔過的一報還一報",即以一定的概率主動停止背叛。群體所有成員處理隨機環境的能力越強,"悔過的一報還一報"效果越好,"寬大的一報還一報"效果越差。
艾克斯羅德通過數學化和電腦化的方法研究如何突破囚徒困境,達成合作,將這項研究帶到了一個全新境界,他在數學上的證明無疑是十分雄辯和令人信服的,而且,他在電腦模擬中得出的一些結論是非常驚人的發現,比如,總分最高的人在每次博弈中都沒有拿到最高分。(劉邦和項羽的戰爭)
艾氏所發現的"一報還一報"策略,從社會學的角度可以看作是一種"互惠式利他",這種行為的動機是個人私利,但它的結果是雙方獲利,並通過互惠式利他有可能覆蓋了範圍最廣的社會生活,人們通過送禮及回報,形成了一種社會生活的秩序,這種秩序即使在多年隔絕,語言不通的人群之間也是最易理解的東西。比如,哥倫布登上美洲大陸時,與印地安人最初的交往就開始於互贈禮物。有些看似純粹的利他行為,比如無償捐贈,也通過某些間接方式,比如社會聲譽的獲得,得到了回報。研究這種行為,將對我們理解社會生活有很重要的意義。
囚徒困境擴展為多人博弈時,就體現了一個更廣泛的問題──"社會悖論",或"資源悖論"。人類共有的資源是有限的,當每個人都試圖從有限的資源中多拿一點兒時,就產生了局部利益與整體利益的衝突。人口問題、資源危機、交通阻塞,都可以在社會悖論中得以解釋,在這些問題中,關鍵是通過研究,制定游戲規則來控制每個人的行為。
艾克斯羅德的一些結論在中國古典文化道德傳統中可以很容易地找到對應,"投桃報李"、"人不犯我,我不犯人"都體現了"tit for tat"的思想。但這些東西並不是最優的,因為"一報還一報"在充滿了隨機性的現實社會生活里是有缺陷的。對此,孔子在幾千年前就說出了"以德報德,以直報怨"這樣精彩的修正策略,所謂"直",就是公正,以公正來回報對方的背叛,是一種修正了的"一報還一報",修正的是報複的程度,本來會讓你損失5分,現在只讓你損失3分,從而以一種公正審判來結束代代相續的報複,形成文明。
但是,艾氏對博弈者的一些假設和結論使其研究不可避免地與現實脫節。首先,《合作的進化》一書暗含著一個重要的假定,即,個體之間的博弈是完全無差異的。現實的博弈中,對策者之間絕對的平等是不可能達到的。一方面,對策者在實際的實力上有差異,雙方互相背叛時,可能不是各得1分,而是強者得5分,弱者得0分,這樣,弱者的報複就毫無意義。另一方面,即使對局雙方確實旗鼓相當,但某一方可能懷有賭徒心理,認定自己更強大,採取背叛的策略能占便宜。艾氏的得分矩陣忽視了這種情形,而這種賭徒心理恰恰在社會上大量引發了零和博弈。因此,程式還可以在此基礎上進一步改進。
其次,艾氏認為合作不需預期和信任。這是他受到質疑頗多之處。對策者根據對方前面的戰術來制定自己下麵的戰術,合作要求個體能夠識別那些曾經相遇過的個體並且記得與其相互作用的歷史,以便作出反應,這些都暗含著"預期"行為。在應付複雜的對策環境時,信任可能是對局雙方達成合作的必不可少的環節。但是,預期與信任如何在電腦的程式中體現出來,仍是需要研究的。
最後,重覆博弈在現實中是很難完全實現的。一次性博弈的大量存在,引發了很多不合作的行為,而且,對策的一方在遭到對方背叛之後,往往沒有機會也沒有還手之力去進行報複。比如,資本積累階段的違約行為,國家之間的核威懾。在這些情況下,社會要使交易能夠進行,並且防止不合作行為,必須通過法制手段,以法律的懲罰代替個人之間的"一報還一報",規範社會行為。這是艾克斯羅德的研究對制度學派的一個重要啟發。
博弈論與非對稱信息博弈論、管理博弈論的比較[1]
博弈論是非對稱信息博弈論與管理博弈論的理論基礎,非對稱信息博弈論與管理博弈論都是博弈論的應用分支。非對稱信息博弈論是非合作博弈論在經濟學上的應用,主要研究非對稱信息結構下的最優契約安排問題;管理博弈論是博弈論和非對稱信息博弈論在管理學中的應用,主要研究多目標、多因素、多階段下的管理激勵與約束機制設計問題。
博弈論偏重方法論研究,局中人地位平等,沒有明確的設計主體,註重定量模型化分析,研究的目的是求得博弈問題的納什均衡解。非對稱信息博弈論主要基於委托—代理理論框架下設計最優交易契約,設計主體為委托人,實施對象為代理人,委托人與代理人之間信息非對稱,委托人通過設計一種激勵機制,使代理人按他所期望的方向行動。
管理博弈論以管理問題為導向,設計主體是管理者,實施對象是被管理者(有限理性人),管理者通過設計和建立有效的激勵與約束機制,激勵、約束、規範被管理者建立有效的激勵與約束機制,激勵、約束、規範被管理者的行為。管理博弈論對管理博弈問題的表述形式主要採用機制式表述,同時,針對具體問題也可靈活應用博弈論的戰略式表述、擴展式表述及非對稱信息博弈論的特征函數式表述。
非對稱信息博弈論與博弈論、管理博弈論的比較
| 1.博弈論(含合作博弈論和非合作博弈論) | 2.非對稱信息博弈論 | 3.管理博弈論 | |
| 本質關係 | 是2、3基礎 | 是非合作博弈論在經濟學上的應用 | 是合作博弈論、非合作博弈論、非對稱信息博弈論在管理學上的應用 |
| 研究著眼點 | 方法論導向 | 經濟問題導向 | 管理問題導向 |
| 研究結果體現 | 綜合信息結構下可能的均衡結果 | 綜合信息結構下的激勵與約束機制設計 | |
| 博弈的一般表達方式 | 戰略式表述;擴展式表述; | 特征函數式表述 | 戰略式表述;擴展式表述;特征函數式表述;機制式表述 |
| 對“機制”的定義 | 博弈框架 | 契約 | 管理系統內各分系統、各要素之間相互
作用、相互聯繫、相互制約的形式及其運動原理和內在的、本質的工作方式 |
| 設計主體 | 不甚明確 | 委托人 | 管理組織 |
| 針對對象 | 不甚明確 | 理性代理人 | 有限性的管理對象(可以是組織、群體或個人) |
| 信息狀況 | 信息分散化 | 信息不對稱 | 信息複雜化、多樣化 |
| 量化情況 | 定量 | 定量 | 定性定量相結合 |
| 施行情況 | 假定施行,但不明確考慮 | 假定施行,且明確考慮 | 假定施行,明確考慮如何施行,且在施行過程中進行評估、修改、完善 |
案例一:博弈論在企業人力資本投資中的應用[2]
一、引言
一個企業能否在市場中取得經濟優勢,依賴於企業科技優勢、產品的市場適應性等等,而這一切又源於人才優勢。因此,一個企業面臨著如何儘可能地保持自己人力資源的優勢,如何吸引優秀人才加入企業添加新動力,如何有效培訓使己有員工獲得技能的提高,如何使員工適應外部環境變化的要求,如何有效輓留公司的核心人才等等。但是統計調查顯示,我國的培訓現狀不盡如人意。總體來看,我國企業培訓管理的制度化、規範化程度有待加強,培訓計劃執行不力,培訓效果跟蹤與評價環節薄弱,培訓對改善員工績效的效用沒有發揮,培訓結果與員工晉升沒有太大影響等。造成這種現狀的原因固然是多方面的,其中一個主要原因就是人力資本投資收益的滯後性和不確定性,擔心員工“硬了翅膀就飛走”,得不償失。企業是否增加人力資本投資,員工是否留任企業,都是利益的博弈,結果是選擇有利於自己的戰略。本文用博弈論對企業人力資本投資作分析,說明企業應當進行人力資本投資和投資後應採取措施保證人力資本投資收益的獲取。
二、概念和假定
1.概念界定
①人力資本。人力資本是通過投資於已有人力資源而形成的、以複雜勞動力為載體的、能實現價值增值的可變資本。
②企業人力資本投資。企業人力資本投資是指企業通過一定的投入(貨幣、資本或實物)獲得人力資源,增加企業員工的知識、技能、健康水平,提高企業管理、文化水平和企業形象,從而提升企業人力資本存量,使企業經濟效益提高的一種投資行為。
2.基本假設
①經濟人。經濟人假設是指無論是組織還是個人,追求自身利益的最大化。
②完全信息。完全信息是指信息是完全通暢的,不存在滯塞,而且客觀存在的信息的獲取是不需要成本的。
③物質資本充足。商品的生產總是物質資本和人力資本結合在一起進行的。
要使生產高效率的進行,物質資本和人力資本必須保持適當的比例。
三、人力資本投資與員工個人的博弈分析
本文從企業與員工之間的角度作人力資本投資的完全信息靜態博弈分析,重點分析企業是否增加人力資本投資以及投資後如何行動。
假定在完全信息的條件下,企業和員工都是理性的。企業可以選擇對員工培訓或不培訓。根據企業的選擇,員工會做出留下或是轉投其他企業的選擇。假設企業不對員工進行培訓是員工的收入為d,當企業選擇培訓,假設分攤到員工個人的培訓費用為c,經過培訓後多支付員工的薪水為e(e可以為零,即經過培訓後不增加員工薪水),經過培訓後員工為企業帶來的收益增加值為b。又假設員工離職去另一單位獲得的報酬為a。這裡為了分析更簡單一些,假設員工經過培訓與未經過培訓跳槽的收入一樣,都為a。有時候培訓後由於員工技能提高跳槽會獲得更多的收入,但是並不影響下麵的分析。企業培訓博弈分析如表1所示: 當b-c-e<0時,即企業對員工培訓後得到的收益增加值小於支出時,不管員工做出如何決策,企業都不會得到任何的收益增加值,因此企業是不會對員工進行培訓投入的。
當b-c-e>0時,該博弈成立並可能會出現兩種均衡:如果此時員工選擇留下所獲得的收益d+e大於其選擇跳槽時所獲的收益a時,理性的員工必定會留在原來的企業,企業也必然會選擇培訓投入,這也是這個博弈中雙方的最優決策;如果此時員工選擇留下所獲得的收益d+e小於其選擇跳槽時所獲的收益a時,理性的員工必定選擇跳槽,此時企業損失為c,損失最慘重。對企業而言,如果知道這樣做令員工跳槽的話,那麼企業還不如剛開始就不培訓,那樣蒙受的損失會少些。這裡需要指出的是,一個員工是否跳槽並不簡單的取決於對方企業開出的薪酬。影響因素有很多,比如員工個性是否與企業匹配、員工個人發展前景、員工興趣與崗位的匹配等等。上述表格中,企業如果不對員工進行培訓,那麼員工留下或離職取決於現有收入d和跳槽企業的薪酬a。
如果d>a,員工留下:反之員工跳槽
總之,員工是否留任企業,是一種利益的博弈,並且企業與員工之間存在著信息的不對稱,企業必須採取先發行動傳遞信號減弱員工離任的動機,只要企業能留住員工,人力資本投資就會給企業帶來巨大的經濟效益。
案例二:博弈論在企業經營活動的應用策略[3]
哈佛商學院的邁克爾·波特教授提出的波特五力分析模型,給出了我們思考行業市場競爭狀況和態勢時一種全面而詳細的分析方法,其中一種力量是潛在進入者的威脅。
那麼,根據市場類型(完全競爭市場、壟斷競爭市場、完全壟斷市場和寡頭壟斷市場),由於多數行業市場屬於壟斷競爭市場,就存在現有企業和新進入者之間的進入和退出博弈,這取決於彼此結構性的進入障礙、對關鍵資源的控制度、規模經濟效應及現有企業的市場優勢的因素。
如果你是現有行業的壟斷者和一定程度的影響者,阻止潛在進入者進入市場或遏止現有企業惡性競爭的博弈策略有:
1.擴大生產能力策略
壟斷者為阻止潛在進入者進入市場,壟斷者可能對潛在進入者進行威脅。但壟斷者的這種威脅是否能達到阻止進入的目的,取決於其承諾。所謂承諾(Promise),是指對局者所採取的某種行動,這種行動使其威脅成為一種令人可信的威脅。那麼,一種威脅在什麼條件下會變得令人可信呢?一般是,只有當對局者在不實行這種威脅會遭受更大損失的時候,與承諾行動相比,空頭威脅無法有效阻止市場進入的主要原因是,它是不需要任何成本的。發表聲明是容易的,僅僅宣稱將要做什麼或者標榜自己是說一不二的人也都缺乏實質性的意義。因此,只有當對局者採取了某種行動,而且這種行動需要較高的成本或代價,才會使威脅變得可信。
2.保證最低價格條款的策略
所謂“保證最低價格”條款策略,即可採取限制性定價策略,通過收取低於進入發生時的價格來防範進入。如某商店規定,顧客在本商店購買這種商品一定時期內(如一個月),如果其他任何商店以更低的價格出售同樣的商品,本店將退還差價,並補償差額的一定百分比(如10% )。例如,如果你在該商店花5 000元購買了一架尼康相機,一周後你在另一家商店發現那裡只賣4500元,那麼你就可以向該商店交涉,並獲得550元的退款。
又如假定一個將存在兩期的市場。在第1期只有一個廠商,面臨兩種選擇:
①制定一個壟斷高價60元,可獲1 000元的利潤,但會使潛在企業認為該行業有利可圖,從而選擇在第2期進入;而一旦該市場有兩個企業存在,將會使市場價格下降到30元,企業利潤降為200元。這樣,兩期的總利潤是1000+200=1200元。
②制定低價40元,潛在企業如果進來,價格降到20元,兩個企業的利潤都將是0。
故此時潛在企業將不會進入。這樣,第二期的價格可以確定一個壟斷高價60元,因此總利潤將為600+1000=1600元。
對消費者來說,保證最低價格條款使你至少在一個月內不會因為商品降價而後悔你的購買,但這種條款對消費者是承諾,對競爭者是警告,無疑是企業之間競爭的一種手段。
保證最低價格條款是一種承諾,由於法律的限制,商店在向消費者公佈了這一條款之後是不能不實行的,因此它是絕對可信的。這一承諾隱含著企業A向企業B發出的不要降價競爭的威脅,並使這種威脅產生其預期的效果。
3.限制進入定價策略
限制進入定價是指現有企業通過收取低於進入發生的價格的策略來防範進入,潛在進入者看到這一低價後,推測出進入後價格也會那麼低甚至更低,因而進入該市場終將無利可圖而放棄進入。
4.掠奪性定價策略
掠奪性定價是指將價格設定為低於成本來達到驅逐其他企業的目的,而期望由此發生的損失在新進入企業或者競爭對手被逐出市場後,掠奪企業能夠行使市場權力時可能得到補償,即在驅逐其他企業後,再制定壟斷高價以彌補前期的損失。這也是一種價格報複策略。掠奪性定價與限制定價之間的差異在於限制定價是針對那些尚未進入市場的企業,是想較長一段時間內維持低價來限制新企業的進入,而掠奪性定價則將矛頭指向已經進入的企業或即將來臨之際。如你產能過剩,在新企業進入時可以進行產能擴張,將商品大幅降價防堵其進入。
5.廣告戰博弈
有些商品只有在使用後才知道其質量真正如何,我們把這種商品稱為經驗品。只有生產那些高質量經驗品的企業才會選擇做巨額廣告,而低質量的企業將不會做廣告。原因是高質量經驗品會有大量的回頭客,而低質量經驗品則鮮有人再次光顧。
另外現有廠商之間產量、價格競爭的博弈,尚有古諾模型、伯川德模型可以描述。博弈理論在巨集微觀層面對企業參與競爭、制定競爭策略均有指導意義。著名營銷專家希頓曾說,企業家的藝術就是對企業的策略性經營和管理,博弈作為策略,企業在當今激烈的市場競爭中需要博弈!
案例三:博弈論在企業管理中的應用[4]
一、博弈論在企業決策中的應用
1.博弈論成果與經營決策
博弈論的研究成果可直接運用於現代企業的經營決策之中。在市場經濟條件下,企業之間的競爭日益加劇,行業內的競爭逐漸表現為幾個大型集團之間的直接對抗。從博弈定義來看,這類問題都可歸結為博弈問題。因此企業運用博弈論中的決策模型進行決策,將使決策過程更加合理化。當今社會,各個方面的競爭性和對抗性日益加劇,人們對自身行為、理性決策和對效率的追求日益增高,現代企業管理充滿了博弈的思想。
2.博弈論與企業最優決策
在社會經濟生活中,企業或個人為了自身利益的最大化,面對市場會做出自己的最優決策,不同的市場情形會影響經濟主體人的決策行為。在完全競爭市場條件下,企業會根據給定商品的市場價格計算出生產和供應到市場上的商品的數量,以實現最大的利潤。而寡頭市場的情形要比完全競爭市場複雜得多。企業大量面對的是信息不完全的市場,企業不知道面對強大的競爭對手該如何做出抉擇,市場的時效性要求企業必須在信息不完全的情況下做出決策。在這樣的決策中存在著三個合理的假設。
第一,理性的“經濟人”。每一個行為主體都依據自身利益的最大化作為行動的出發點。
第二,每一個行為主體做出的決策都不是在真空的世界中。現實的世界使得一個人的生存必須以他人的生存為前提。這種相互依賴的關係使得一個行為主體的決策會對其他行為主體產生重要的影響,其他行為主體的決策也會直接影響著這個行為主體的決策結果。
第三,寡頭市場的情形。也即一個行業裡面只有少數幾家企業,甚至只有兩三家企業,每一方的市場份額都很大。由於競爭對手很少,每一個主體的行為產生的後果受對手行為的影響都很大。那麼這樣的決策就帶有了博弈的色彩。
3.博弈均衡理論與企業決策
企業決策要充分考慮均衡,博弈論的精髓在於其中的任何一個理性決策者,必須考慮在其他局中人反應的基礎上來選擇自己最理想的行動方案。所謂均衡,即所有局中參與人的最優策略組合,各方博弈產生的結果是一個均衡結局,它可能不是局中各方及整體的利益最大化,但它是在已給定信息與知識條件下的一種必然結果,因為任何一方改變策略而導致均衡的變化都有可能使自己得到一個更差的結果。近來,人們越來越重視博弈論在市場競爭過程中的作用,人們正在通過調整決策,避免衝突以尋求合作,實現共贏,規避雙輸。
二、博弈論在構建和諧企業中的應用
博弈論的研究成果,提高了人們對競爭和衝突這一社會現象的認識,對於我們在現實生活中如何運用合作的理念,創建和諧企業具有重要的啟示和作用。企業作為社會的組成單元,在構建社會主義和諧社會中承擔著義不容辭的責任。對企業來說,“和諧”的基本特征應當表現為依法治企、科學發展、協調有序、安全環保、公平誠信、服務社會,並建立一個長效的協調機制,其核心在於通過促進企業內外環境的“和諧”,達到企業的經濟效益與社會效益相統一,最終實現企業健康、協調、可持續發展。
1.處理好個人、集體和國家的利益關係
在市場經濟中,個人、企業和政府都會追求自己的利益,在各自的運轉環境中,實際上都處於博弈狀態,各自都是在現實生活環境中的博弈一方,衝突和矛盾是難免的。隨著國有企業改革的不斷深化,在股份制改造和現代化企業制度建設過程中,輪崗、下崗、合併、重組等問題所引發的分工、收入、保障的差距越來越成為矛盾的焦點。掩蓋這種利益的差別,否認博弈的現實並不能解決問題。所以,需要客觀地看待這些差別。
2.處理好博弈與規則透明、誠實守信的關係
規則透明和誠實守信是博弈各方達成協議的基礎,規則透明是互信的條件。管理者要想取得人們的信任,政策必須公開、公正。對於企業,企業管理者要取得職工的信任和擁護,企業要在市場上立得住、站得穩,必須講誠信、講公平、講公正。如果所要的結果不是通過透明、可信的規則取得的,必然不會與職工群眾達成共識,企業氛圍也不會是和諧的、穩定的。
3.處理好博弈過程中利益各方的關係
和諧企業建立的基礎是企業各方面的共贏,博弈各方達成的協議雖然未必是利益均等,但應該是各方面都能接受的。建立和諧企業,需要從根本上、制度上解決問題,而制度的建立、措施的完善應建立在科學的基礎上,建立在各方都能接受的共贏的基礎上,而不是企業方想怎樣做就怎樣做。如果不能保證各方共贏,必然得不到其他方面的支持,那它必然是不穩定的、不和諧的,甚至會導致更多、更嚴重的問題。
4.處理好經濟利益之外的博弈關係
和諧不完全建立在經濟利益上,除此之外仍然有很多人文因素影響著社會的和諧。因此,企業管理者的充分溝通、理解職工的非經濟期望和需求,給予人文關懷,對於促進和諧社會的形成有著不可忽視的作用。
三、博弈論在企業價格戰中的應用
在現實生活中,我們經常會遇到各種各樣的價格大戰,如彩電大戰、冰箱大戰、空調大戰等,這些大戰的受益者首先是消費者。在這裡,廠家價格大戰的結局是一個“納什均衡”,而且價格戰的結果是誰都沒賺到錢,因為博弈雙方的利潤正好是零。這個結果可能對消費者是有利的,但對廠商而言是災難性的。所以,價格戰對於廠商而言意味著自殺。從中我們可以引申出兩個問題,一是競爭削價的結果或“納什均衡”可能導致一個零利潤結局;二是如果不採取價格戰,作為一種敵對博弈論其結果有兩種,一種是企業採取正常價格策略,另一種是採取高價格策略形成壟斷價格。事實上,完全競爭的均衡就是“納什均衡”或“非合作博弈均衡”。在這種狀態下,沒一個廠商或者消費者是按照別人已定的價格來進行決策。在這種均衡中,企業要使利潤最大化,消費者要使效用最大化,結果導致了零利潤,也就是說價格等於邊際成本。
- Harold W. K.(editor), 1997, Classics in Game theory, Princeton, NJ:Princeton University Press ISBN 0691011931
- Myerson, R., 1991, Game Theory: Analysis of Conflict. Cambridge and London: Harvard University Press.
- Osborne, M. and A. Rubinstein,1994,A Course in Game Theory, Cambridge and London: The MIT Press.
- Axelrod, Robert: The Evolution of Cooperation, 1985, ISBN 0465021212
- Axelrod, Robert: The Complexity of Cooperation - Agent-Based Models of Competition and Collaboration, 1997, ISBN 0691015678
- Dixit, Avinash K./ Skeath, Susan: Games of Strategy, 1999, ISBN 0393974219
- Eigen, Manfred / Winkler, Ruthild: Das Spiel, 1976, ISBN 3492021514
- Hargreaves Heap, Shaun P. / Varoufakis, Yanis: Game Theory - A Critical Text, 2004, ISBN 0415250951
- Kelly, Anthony: Decision Making Using Game Theory - An Introduction for Managers, 2003, ISBN 0521814626
- Schlee, Welter: Einführung in die Spieltheorie, 2004, ISBN 3528032146
- 清華大學博弈論講義
本条目由以下用户参与贡献
Vulture,苦行者,JACK,Hanmlate,Lolo,沙漠之鹰,001,Freeman96300,Angle Roh,Lteco,Zfj3000,Hackerdd,Aidehu,Dan,Zhoujinsong-zjs,Andoup,Cabbage,何飞,Hfowq,郑文辉,ROURTW,Leejunjay,Yixi,Will hu,刘卫坤,Hooy,Hwqo,Hwoeh,鲈鱼,黄文书,雷山,泡芙小姐,Lulushow0823,tuzhenpeng,东风,连晓雾,Gaoshan2013,Mis铭,大侠,金龙,Lin,john,Tracy,LuyinT,刘维燎,M id ba5ba56cc8d8aaf4ab2ba7e3de3f511d.評論(共149條)
用“納什均衡”來挑戰斯密的“看不見的手”原理,不但是自己無知的表現,也是別有用心的表演!
“納什均衡”的囚徒博弈是一次性博弈,“看不見的手”是無限博弈;“納什均衡”的囚徒博弈是非合作性(非社會性)博弈,而“看不見的手”是合作性(內生社會性)的博弈!
編輯者無知,動不動就挑戰?
用“納什均衡”來挑戰斯密的“看不見的手”原理,不但是自己無知的表現,也是別有用心的表演!
“納什均衡”的囚徒博弈是一次性博弈,“看不見的手”是無限博弈;“納什均衡”的囚徒博弈是非合作性(非社會性)博弈,而“看不見的手”是合作性(內生社會性)的博弈!
編輯者無知,動不動就挑戰?
同志您的分析完全錯誤 對博弈論的瞭解也很錶面 1.大眾所知的困徒博弈 裡面有“拿殊均衡” 而你的原話 “納什均衡”的囚徒博弈是一次性博弈 “拿殊均衡”不是困徒博弈的 這個是天大的錯誤 2.“看不見的手”的對象所處的環境 站在博弈角度來看 絕對不只是無限博弈 這個也是天大的錯誤
~編者所說的挑戰 是從“無形的手”的市場原理-人無可奈何 到 “拿殊均衡” 加入了人的意志在策略上斟酌 這絕對是對使用百年的經濟學理論的挑戰 再次強調一下 你要說 就只能說 困徒博弈是非合作博弈
用“納什均衡”來挑戰斯密的“看不見的手”原理,不但是自己無知的表現,也是別有用心的表演!
“納什均衡”的囚徒博弈是一次性博弈,“看不見的手”是無限博弈;“納什均衡”的囚徒博弈是非合作性(非社會性)博弈,而“看不見的手”是合作性(內生社會性)的博弈!
編輯者無知,動不動就挑戰?
低水平 裝老大.....你才是無知誤導大眾 “拿殊均衡”是可以推廣到 有連續得益函數的無限博弈中。 證明策略空間是歐幾里德空間的非空緊凸子集的策略性博弈,如果有連續和擬凹的得益函數,就一定存在純策略下的拿殊均衡(Debreu,1952;Glickerg,1952;Fan,1952)
愛情博弈學——獲得幸福愛情的博弈原則 戀人,既是你的合作伙伴,也是你的對手,甚至敵人。在戀愛的這場不太好玩的“游戲”中,誰能熟練地駕御游戲或博弈規則,誰就是愛情的贏家。所以,要想成為贏家,就要學會與伙伴一樣的戀人合作,還要學會與敵人一樣的戀人周旋。面對對手圍追堵截的愛情圍剿,要學會閃轉騰挪的諸多反圍剿的手段。按照囚徒困境的分析結論,戀人最得意的選擇是另覓新歡,最天真的選擇是天荒地老,最理性的選擇是分道揚鑣,最糟糕的選擇是被另有新歡的對方無情拋棄。問題是,最得意的結局過於缺德,最天真的結局過於虛幻,最理性的結局過於殘酷,最糟糕的結局又(讓一方)過於心痛。
人生髮誓最多的時期,大概就是戀愛期。發什麼誓呢?無非是什麼非你不娶非你不嫁你是風兒我是沙啊的一類誓言罷了,目的只有一個,就是讓對方相信自己能夠天荒地老而此情不渝。他們希望彼此忠誠,從而換來一個好的博弈結果。
而且,為了防止對方變心,總要設法讓對方相信,你遇到我是你三生有幸,而我遇到你也是萬世不毀。可是,世間沒有什麼誓約是永恆的。很多愛情的悲劇,往往都從背棄誓約開始,而天下又似乎沒有沒有誓約的愛情。
然而,這個結論在實際上是有問題的。因為,生活中戀愛成功的人並不少見,廝守一生一世的人也不少見,不能說他們都是勉強的。事實上,他們有的還的確生活得很幸福。
那麼,在這個重覆博弈的過程中,誰將是情場上的贏家呢?誰將在博弈中獲勝呢?
獲得幸福愛情的博弈原則應該是:
第一,善意而不是惡意地對待戀人。這個道理很簡單了,無須多說。
第二,寬容而不是尖刻地對待戀人。幸福的戀人可能並不是忠貞不二的,當然也肯定不是見異思遷的,他們能夠生活得愉快,關鍵是能夠彼此寬容,既寬容對方的缺點,甚至也寬容他偶爾的不忠貞。而尖刻地對待戀人的人,對戀人的偶爾不忠貞總是不肯遷就的人,往往也都不會幸福。
第三,強硬而不是軟弱地對待戀人。就是要在我永遠愛你的善意的前提下,做到有愛必報,有恨也必報,以眼還眼,以牙還牙,以其人之道,還治其人之身。這其中,當然是要有限度和分寸的。
第四,簡單明瞭而不是山環水繞地對待戀人。在博弈過程中,過分複雜的策略使得對手難於理解,無所適從,因而難以建立穩定的合作關係。事實上,在一個非零和的環境里,“城府深嚴”、“兵不厭詐”、“揣著明白裝糊塗”往往並非上策。相反,明晰的個性、簡練的作風和坦誠的態度倒是制勝的要訣。要讓戀人明白你說的是什麼,切忌讓對方猜來猜去的,造成誤會。因為不簡單明瞭地對待戀人最終導致誤會而分手的愛情悲劇並不少啊。所以,愛情的手段,還是簡單一點好,讓戀人一看就明白,免去了很多猜謎的時間!
情場贏家的結論:勝利也總是屬於那些善意的、寬容的、強硬的、簡單明瞭的戀人們。反之,愛情將最終走向失敗。
雖然捧著一大本的<博奕論>理論書看得頭暈眼花,但我還是很沉迷其中,很多生活中的事情都可以用比較正確地去分析它,讓我在做決策的時候有了更科學的依據.好書!
愛情博弈學——獲得幸福愛情的博弈原則 戀人,既是你的合作伙伴,也是你的對手,甚至敵人。在戀愛的這場不太好玩的“游戲”中,誰能熟練地駕御游戲或博弈規則,誰就是愛情的贏家。所以,要想成為贏家,就要學會與伙伴一樣的戀人合作,還要學會與敵人一樣的戀人周旋。面對對手圍追堵截的愛情圍剿,要學會閃轉騰挪的諸多反圍剿的手段。按照囚徒困境的分析結論,戀人最得意的選擇是另覓新歡,最天真的選擇是天荒地老,最理性的選擇是分道揚鑣,最糟糕的選擇是被另有新歡的對方無情拋棄。問題是,最得意的結局過於缺德,最天真的結局過於虛幻,最理性的結局過於殘酷,最糟糕的結局又(讓一方)過於心痛。
人生髮誓最多的時期,大概就是戀愛期。發什麼誓呢?無非是什麼非你不娶非你不嫁你是風兒我是沙啊的一類誓言罷了,目的只有一個,就是讓對方相信自己能夠天荒地老而此情不渝。他們希望彼此忠誠,從而換來一個好的博弈結果。
而且,為了防止對方變心,總要設法讓對方相信,你遇到我是你三生有幸,而我遇到你也是萬世不毀。可是,世間沒有什麼誓約是永恆的。很多愛情的悲劇,往往都從背棄誓約開始,而天下又似乎沒有沒有誓約的愛情。
然而,這個結論在實際上是有問題的。因為,生活中戀愛成功的人並不少見,廝守一生一世的人也不少見,不能說他們都是勉強的。事實上,他們有的還的確生活得很幸福。
那麼,在這個重覆博弈的過程中,誰將是情場上的贏家呢?誰將在博弈中獲勝呢?
獲得幸福愛情的博弈原則應該是:
第一,善意而不是惡意地對待戀人。這個道理很簡單了,無須多說。
第二,寬容而不是尖刻地對待戀人。幸福的戀人可能並不是忠貞不二的,當然也肯定不是見異思遷的,他們能夠生活得愉快,關鍵是能夠彼此寬容,既寬容對方的缺點,甚至也寬容他偶爾的不忠貞。而尖刻地對待戀人的人,對戀人的偶爾不忠貞總是不肯遷就的人,往往也都不會幸福。
第三,強硬而不是軟弱地對待戀人。就是要在我永遠愛你的善意的前提下,做到有愛必報,有恨也必報,以眼還眼,以牙還牙,以其人之道,還治其人之身。這其中,當然是要有限度和分寸的。
第四,簡單明瞭而不是山環水繞地對待戀人。在博弈過程中,過分複雜的策略使得對手難於理解,無所適從,因而難以建立穩定的合作關係。事實上,在一個非零和的環境里,“城府深嚴”、“兵不厭詐”、“揣著明白裝糊塗”往往並非上策。相反,明晰的個性、簡練的作風和坦誠的態度倒是制勝的要訣。要讓戀人明白你說的是什麼,切忌讓對方猜來猜去的,造成誤會。因為不簡單明瞭地對待戀人最終導致誤會而分手的愛情悲劇並不少啊。所以,愛情的手段,還是簡單一點好,讓戀人一看就明白,免去了很多猜謎的時間!
情場贏家的結論:勝利也總是屬於那些善意的、寬容的、強硬的、簡單明瞭的戀人們。反之,愛情將最終走向失敗。
我很同意你的觀點!
這樣的深奧理論為什麼不是中國人最早提出來?
為什麼問這樣的問題?!
提出一點編輯上的錯誤,也許是筆誤吧, 在“博弈論的基本概念”這一部分的下麵一段話: “ 這樣,“均衡偶”的明確定義為:一對策略a*(屬於策略集A)和策略b*(屬於策略集B)稱之為均衡偶,對任一策略a(屬於策略集A)和策略b(屬於策略集B),總有:偶對(a, b*)≤偶對(a*,b*)≤偶對(a*,b)。 ” 最後一個小於等於號是不是應該改成大於等於號 望編輯者更正
提出一點編輯上的錯誤,也許是筆誤吧, 在“博弈論的基本概念”這一部分的下麵一段話: “ 這樣,“均衡偶”的明確定義為:一對策略a*(屬於策略集A)和策略b*(屬於策略集B)稱之為均衡偶,對任一策略a(屬於策略集A)和策略b(屬於策略集B),總有:偶對(a, b*)≤偶對(a*,b*)≤偶對(a*,b)。 ” 最後一個小於等於號是不是應該改成大於等於號 望編輯者更正
感謝您的指正,現已對內容進行了更正,MBA智庫是可以自由編輯的,您也可以直接參考編輯修改。
"任何具有有限純策略的二人博弈至少有一個均衡偶",什麼叫有限純策略?對納什均衡還是有點犯暈,哪位大師幫小的詳細解釋一下,舉例解釋也行,小的在此謝過了
提出一點編輯上的錯誤,也許是筆誤吧, 在“博弈論的基本概念”這一部分的下麵一段話: “ 這樣,“均衡偶”的明確定義為:一對策略a*(屬於策略集A)和策略b*(屬於策略集B)稱之為均衡偶,對任一策略a(屬於策略集A)和策略b(屬於策略集B),總有:偶對(a, b*)≤偶對(a*,b*)≤偶對(a*,b)。 ” 最後一個小於等於號是不是應該改成大於等於號 望編輯者更正
這個不等式比較的是選擇的可能性還是利益最大化呢?我沒看明白
怎麼說呢,我是學經濟學的。博弈論確實很有魅力的,他會讓明白很多自然的選擇。學習它的前提是經濟人的假設,但是真的有那麼多經濟人嗎?肯定不是,人都是有感情、有思想的人,在明白這些理論的基礎之上,還應該考慮一些社會學的東西,才會讓你看待事情更加明白。
一個足球愛好者,正在家中看一場世界盃決賽,賽程剛開始就發現自己肚子非常饑餓,雖然下樓花上三分鐘就能夠吃上快餐面了,但又放不下精彩的足球賽,滿足視聽還是滿足食欲,孰重孰輕?很是矛盾,很讓他上火…… 請教,如何運用博弈論來給他找到一個最優的策略?
一個足球愛好者,正在家中看一場世界盃決賽,賽程剛開始就發現自己肚子非常饑餓,雖然下樓花上三分鐘就能夠吃上快餐面了,但又放不下精彩的足球賽,滿足視聽還是滿足食欲,孰重孰輕?很是矛盾,很讓他上火…… 請教,如何運用博弈論來給他找到一個最優的策略?
一個足球愛好者,正在家中看一場世界盃決賽,賽程剛開始就發現自己肚子非常饑餓,雖然下樓花上三分鐘就能夠吃上快餐面了,但又放不下精彩的足球賽,滿足視聽還是滿足食欲,孰重孰輕?很是矛盾,很讓他上火…… 請教,如何運用博弈論來給他找到一個最優的策略?
+++++++++++++++++++++++++++++++++++++++++++++++++++++ 我想這個球迷是不是可以給樓下的餐館打個電話,叫餐館把飯菜送到家裡來?
智豬博弈比較有意思 囚徒困境主要研究的就是人的心理 一切事物均由心生
這當然不是 整個博弈論都是建立在利己的假設基礎之上的 囚徒困境和智豬博弈都是在這一基礎之上 即不論是豬還是人都是要做出利己選擇的 在囚徒困境中只是一種最原始的立即選擇就像豬要吃東西一樣
吵架的人都滾蛋,沒素質
道理越辯越明,你才是沒素質的表現呢
上課的時候幾次看到過這個博弈理論 但是我不是主修經濟的 看了一個多星期才算是看完了 包括裡面的一些術語 當時看的時候 沒明白經濟人假設是什麼一回事(還是百思不得解啊) 但是好不容易看完的時候 才發現在現實生活要很好的運用博弈論的話 還真的不容易 假設 1,你的對手不按該理論與你競爭怎麼才能贏? 2,你(只是泛指沒有特指,會一點理論或是中等以上,反正不是高手)的對手或伙伴是一個比你強的人,在理論上,你要是用博弈論的話那後果就可想而知了 就像我們經濟學老師說的那樣:他是學經濟的結果炒股還沒朋友(沒學過經濟的)炒得好,一樣
不管怎麼樣人還是不可能完全的做到經濟人的,而且人活得太理性了那就不是自己的想法了,或許就不是自己的最大利益了 不過這個博弈論還是吸引了我 很強大的理論 能讓我從另一個角度來看待事物,角度的不同我可以發現一些沒有過的認識和看法。還是很有意思的一門科學。
以上只是一名博弈論愛好者的學習有感 只是我的一些看法 若有更厲害的人(在博弈論上)希望所加點評 謝謝
為什麼要博弈了,人生嘛真就好 了 ,這東西還是 不要用在感情方面,真的
不是用不用的問題,而是它的規律本來就存在於生活中的方方面面!你說的“真”其實就了你自己運用的一種博弈策略而已,只能可能你沒有意識到他是一種博弈的策略!
在自己最矛盾的時候,在這看到博弈的文章,讓我平靜了很多,生活中本來就很博弈,習之以為本,生活就簡單很多,麻煩的是在博弈的過程中。很累……
博弈論的經典模型很有意思,是個值得研究的理論。對於業餘學習者來說更應結合實際情況來理解理論,如專從學術角度去研究的話就太抽象了,我看過博弈論的純理論書,看不懂。怪不得納什是個瘋子,能些出這種東西,強悍!
一個足球愛好者,正在家中看一場世界盃決賽,賽程剛開始就發現自己肚子非常饑餓,雖然下樓花上三分鐘就能夠吃上快餐面了,但又放不下精彩的足球賽,滿足視聽還是滿足食欲,孰重孰輕?很是矛盾,很讓他上火…… 請教,如何運用博弈論來給他找到一個最優的策略?
這個問題很有趣啊,但是看起來這個問題應該歸結於機會成本的概念:選擇A,失去B的機會而所付出的成本。
strategies 拼錯了。
沒錯吧?策略strategy的複數形式
有沒有這方面的書,叫什麼名字??我沒去查,希望能有人直接告訴我一兩本比較好的!
杜塔的《策略與博弈》,活爾*活森《策略》。
用“納什均衡”來挑戰斯密的“看不見的手”原理,不但是自己無知的表現,也是別有用心的表演!
“納什均衡”的囚徒博弈是一次性博弈,“看不見的手”是無限博弈;“納什均衡”的囚徒博弈是非合作性(非社會性)博弈,而“看不見的手”是合作性(內生社會性)的博弈!
編輯者無知,動不動就挑戰?
你無知吧兄弟·納什均衡論的出現一度動搖了西方經濟管理學的基石·納什本人是個很高尚的人· 他幾乎為了納什均衡奉獻了他的一生·如果不是他有精神分裂·他是不會和任何一個人分享他 的諾貝爾獎的成就·納什均衡早就廣泛用於現在社會的各行各業·所以要正確的看待·情況不一樣你 用不一樣的就行了·何必計較那麼多呢·
我想以博弈論在企業中的應用為題寫一篇論文,可以具體到某一問題,但是博弈論確實有點難,希望大家不吝指教,感激不盡!我的是707174399
好,大學就應該開點這樣的課。很有意思,好好玩啊。
耶魯有博弈論的公開課,網上可以看。
我們應用科學發展觀的博弈哲學思想,闡明瞭博弈論、矛盾論、概率論的戰術性質。 博弈論是二人對局,一個叫決策人,一個稱對抗者。 矛盾論是兩個同性質的二人對決。 概率論則是通過二人對局的個數之比得出。 博弈論、矛盾論、概率論各自都是兩個相同性質的對決只能提供經驗,只有對實體與性質的區分才能稱為知識。西方文化大宗教理論都是極其渺小的個體性質的戰術屬性,決不能處理博弈實體里的戰略。在任何博弈實體的系統里,在具體事件中,用矛盾論建立的二人博弈對局都是在悖論中自圓其說,都不能通達博弈實體的事實真相。博弈論、矛盾論、概率論這些文化大宗教理論已經不能解決未來博弈實體里的文明,到了極不正常的歷史死亡階段。因為這些抄來抄去的非物質文化概念,界定模糊,無法定性,無法區分,無法操作,無法驗證,不能證明,又不能證偽。它讓人沒有自在,沒有自我,沒有哲學,更沒有科學。科學不是為哪個階級服務的,科學是大自然前進的規則,科學又像似監工,《博弈聖經》中說:“科學是專門批判他人的。”任何邪惡和迷信都會後退,科學的任務是如實地讓人們認識自然本來的面貌。粒子行為論、國正論、國邊常數1.992187是對政府和人民的提醒,也是讓懷疑論者百口難辨。博弈基因取勝的理論會引發更多人對戰略文化的思考,高熵賽棋這個模型一旦有取勝的理論被驗證,那些無知又無聊的一維思想,那些忽悠人的博弈論、矛盾論、概率論將被徹底否決。《貨幣的威力》一書中說:“哪裡有生命,哪裡就有事件的開端。哪裡有矛盾,哪裡就有死亡。哪裡有非絕對對對立的國正論,哪裡就有粒子行為的碰壁而終結,哪裡就有新體制、新結構和新事物的創生。” 21世紀是科學發展觀的時代,與此同時各種錯誤的觀念都在轉變。未來的專家不必用圍棋、象棋和多米諾骨牌表示博弈對局,這些都不是博弈的實戰模型。那些在媒體上拿著棋子在棋盤上比來比去做廣告的人,沒有一個人能講出什麼是戰略,什麼是戰術,什麼是決策人和對抗者,他們怎麼能單方占優,怎麼才能贏。更為滑稽的是,一個博弈論專家、矛盾論專家、概率論專家,竟沒有創造一個詞,也沒發明一句經典的話,更不要說定理、定律、定義和法則,無論怎麼樣吹捧他們的博弈論著作,竟沒有一個人敢公開說怎麼贏。未來的政治家、軍事家不能僅僅喊幾句博弈口號或知道一點散落在民間的博弈小常識和幾個博弈辭彙,也不是講幾個博弈的小故事。如果不知道高熵賽棋具有極其重要的軍事戰略文化價值,沒有真正用高熵賽棋的二人對局對其進行深入地實戰性研究,就不知道在二人對局中如何戰勝對手,更不知道在未來的大博弈中取勝,對一個國家的各級CEO,那將是一個災難性的未來。《博弈聖經》上說:“21世紀博弈的大事是精確地測量,科學家可以對未來100年的科學進行預測,沒有一個人敢預測博弈的未來,可見難度非同一般。不經過測量的東西是粗糙的、雜亂的、不符合意願的、難以控制的。”《博弈聖經》闡述的理論和高熵賽棋,這不是虛構的文學故事,也不是官員的形式空話,更不是大學里抄來的論文,這是公開於世的發現,它所有的理論都受到知識產權的法定保護。
愛情博弈學——獲得幸福愛情的博弈原則 戀人,既是你的合作伙伴,也是你的對手,甚至敵人。在戀愛的這場不太好玩的“游戲”中,誰能熟練地駕御游戲或博弈規則,誰就是愛情的贏家。所以,要想成為贏家,就要學會與伙伴一樣的戀人合作,還要學會與敵人一樣的戀人周旋。面對對手圍追堵截的愛情圍剿,要學會閃轉騰挪的諸多反圍剿的手段。按照囚徒困境的分析結論,戀人最得意的選擇是另覓新歡,最天真的選擇是天荒地老,最理性的選擇是分道揚鑣,最糟糕的選擇是被另有新歡的對方無情拋棄。問題是,最得意的結局過於缺德,最天真的結局過於虛幻,最理性的結局過於殘酷,最糟糕的結局又(讓一方)過於心痛。
人生髮誓最多的時期,大概就是戀愛期。發什麼誓呢?無非是什麼非你不娶非你不嫁你是風兒我是沙啊的一類誓言罷了,目的只有一個,就是讓對方相信自己能夠天荒地老而此情不渝。他們希望彼此忠誠,從而換來一個好的博弈結果。
而且,為了防止對方變心,總要設法讓對方相信,你遇到我是你三生有幸,而我遇到你也是萬世不毀。可是,世間沒有什麼誓約是永恆的。很多愛情的悲劇,往往都從背棄誓約開始,而天下又似乎沒有沒有誓約的愛情。
然而,這個結論在實際上是有問題的。因為,生活中戀愛成功的人並不少見,廝守一生一世的人也不少見,不能說他們都是勉強的。事實上,他們有的還的確生活得很幸福。
那麼,在這個重覆博弈的過程中,誰將是情場上的贏家呢?誰將在博弈中獲勝呢?
獲得幸福愛情的博弈原則應該是:
第一,善意而不是惡意地對待戀人。這個道理很簡單了,無須多說。
第二,寬容而不是尖刻地對待戀人。幸福的戀人可能並不是忠貞不二的,當然也肯定不是見異思遷的,他們能夠生活得愉快,關鍵是能夠彼此寬容,既寬容對方的缺點,甚至也寬容他偶爾的不忠貞。而尖刻地對待戀人的人,對戀人的偶爾不忠貞總是不肯遷就的人,往往也都不會幸福。
第三,強硬而不是軟弱地對待戀人。就是要在我永遠愛你的善意的前提下,做到有愛必報,有恨也必報,以眼還眼,以牙還牙,以其人之道,還治其人之身。這其中,當然是要有限度和分寸的。
第四,簡單明瞭而不是山環水繞地對待戀人。在博弈過程中,過分複雜的策略使得對手難於理解,無所適從,因而難以建立穩定的合作關係。事實上,在一個非零和的環境里,“城府深嚴”、“兵不厭詐”、“揣著明白裝糊塗”往往並非上策。相反,明晰的個性、簡練的作風和坦誠的態度倒是制勝的要訣。要讓戀人明白你說的是什麼,切忌讓對方猜來猜去的,造成誤會。因為不簡單明瞭地對待戀人最終導致誤會而分手的愛情悲劇並不少啊。所以,愛情的手段,還是簡單一點好,讓戀人一看就明白,免去了很多猜謎的時間!
情場贏家的結論:勝利也總是屬於那些善意的、寬容的、強硬的、簡單明瞭的戀人們。反之,愛情將最終走向失敗。
關於強硬這個東西,我自身的理解是,在戀愛雙方(當然,也有多方)應該會有個你微強我微弱的狀態,她強,他也強,你強我強,那戀愛就不強了。男人在女人面前胸懷像大海,這樣比較好,寬容和強硬貌似有那麼一點的關係,當然,在對待一些自己底線的事情上,得強硬。 在對待戀愛的態度上,我一直堅持的觀念是:能走就走,走不了就散。 祝大家都有個美好的戀愛!
《博弈聖經》中《人類未知的藍色檔案》一文給出了博弈論的定義:“我們把動物利用大自然移動的癮魂,在決策人期待的空間里,形成相對均衡的語文學理論,稱為博弈論。”
目前,博弈的形式仍是直接強權、威懾、恐嚇、掠奪,只知道殘暴地把棒子加粗、炮加大。實際上,粗暴的簡單性成了各國首腦和軍事家之間顯示博弈優勢的全部思維和博弈行為的直接內容。
《博弈聖經》中《人類未知的藍色檔案》一文中寫道:“誰能讓現代的博弈行為接近野蠻,誰能讓友善與凶殘之間的距離大到令人不解,誰就在博弈中取勝。”
科學發展觀的定義中使用了“民主”一詞,《博弈聖經》中對民主有這樣一段陳述: “民主是一種原始個體主義對集體的訴求,民主要求嚴格的法則和博弈的自由。 民主是優先喚醒,是對未來希望的擁有。 民主是平等的人權給以精神的回歸。 任何民主,都是想把統治者馴服關在民主的籠子里。 每一個人對民主意願的訴求,都是主動鑽進了民主的籠子,讓 【博弈實體政治】的威力高於一切。”
一個足球愛好者,正在家中看一場世界盃決賽,賽程剛開始就發現自己肚子非常饑餓,雖然下樓花上三分鐘就能夠吃上快餐面了,但又放不下精彩的足球賽,滿足視聽還是滿足食欲,孰重孰輕?很是矛盾,很讓他上火…… 請教,如何運用博弈論來給他找到一個最優的策略?哈哈,打個電話讓送外賣來,即可!
送外賣的來後,給錢,可送外賣的說,沒零錢找!可又不願意再跑一趟去換零錢,這是,送外賣的說:我幫你看著,你去換一下零錢,進球了,我回頭告訴你!你別急,反正我告訴你,世界盃(南非)我們中國隊是進不了的!要等等等等,千萬別餓著自己!
對於“囚徒的困境”的我有不同的看法,如果兩名囚徒都認為富人該死而寧願自己多做牢而對方少坐牢呢?或者說彼此信任對方不會出賣自己都同時抵賴呢?那就是最優抉擇。所以我認為應該建立法治化游戲規則。讓每個人都得有信托責任,才能達到帕累托最佳。而亞當斯密所說的國富論就是這樣。不要誤讀了,那些只是錶面現象,而亞當斯密的看不見的手的前提就是每個人都得有信托責任才來的。你認為納什均衡和看不見的手相悖就是因為你的血液每有信托責任。而納什均衡一樣證明著每個人都要有信托責任的重要。
一個足球愛好者,正在家中看一場世界盃決賽,賽程剛開始就發現自己肚子非常饑餓,雖然下樓花上三分鐘就能夠吃上快餐面了,但又放不下精彩的足球賽,滿足視聽還是滿足食欲,孰重孰輕?很是矛盾,很讓他上火…… 請教,如何運用博弈論來給他找到一個最優的策略?
+++++++++++++++++++++++++++++++++++++++++++++++++++++ 我想這個球迷是不是可以給樓下的餐館打個電話,叫餐館把飯菜送到家裡來?
再接著問一下,樓下餐館里的人也在看球賽,那到底是要賺錢還是接著看比賽(餐館就只有一人的情況下)
我看了這麼多, 最後我想說,上面那位仁兄舉出的足球愛好者去不去買飯這個案例,我認為不屬於博弈論里,不是所有的現實都能說成博弈論,或者都能用博弈論來尋找最優,連三個建立博弈模型的要素都達不到,如何用博弈論解釋?
利益的最大化了,這是博弈里決策的基礎,簡單點就是理性人在決策時追求個人收益最大化。
對於“囚徒的困境”的我有不同的看法,如果兩名囚徒都認為富人該死而寧願自己多做牢而對方少坐牢呢?或者說彼此信任對方不會出賣自己都同時抵賴呢?那就是最優抉擇。所以我認為應該建立法治化游戲規則。讓每個人都得有信托責任,才能達到帕累托最佳。而亞當斯密所說的國富論就是這樣。不要誤讀了,那些只是錶面現象,而亞當斯密的看不見的手的前提就是每個人都得有信托責任才來的。你認為納什均衡和看不見的手相悖就是因為你的血液每有信托責任。而納什均衡一樣證明著每個人都要有信托責任的重要。
這裡不是說理性的對抗者和決策者麽!你說的是感情,這是不符合模型條件的!
再接著問一下,樓下餐館里的人也在看球賽,那到底是要賺錢還是接著看比賽(餐館就只有一人的情況下)
再打電話到其他餐館。
有這樣的書就好了
有關於博弈論的書的,你可以上卓越看一下。
上課的時候幾次看到過這個博弈理論 但是我不是主修經濟的 看了一個多星期才算是看完了 包括裡面的一些術語 當時看的時候 沒明白經濟人假設是什麼一回事(還是百思不得解啊) 但是好不容易看完的時候 才發現在現實生活要很好的運用博弈論的話 還真的不容易 假設 1,你的對手不按該理論與你競爭怎麼才能贏? 2,你(只是泛指沒有特指,會一點理論或是中等以上,反正不是高手)的對手或伙伴是一個比你強的人,在理論上,你要是用博弈論的話那後果就可想而知了 就像我們經濟學老師說的那樣:他是學經濟的結果炒股還沒朋友(沒學過經濟的)炒得好,一樣
不管怎麼樣人還是不可能完全的做到經濟人的,而且人活得太理性了那就不是自己的想法了,或許就不是自己的最大利益了 不過這個博弈論還是吸引了我 很強大的理論 能讓我從另一個角度來看待事物,角度的不同我可以發現一些沒有過的認識和看法。還是很有意思的一門科學。
以上只是一名博弈論愛好者的學習有感 只是我的一些看法 若有更厲害的人(在博弈論上)希望所加點評 謝謝
經紀人的假設是斯密提出的 即假設所有經濟活動參與者都是“理性人”,其所有行為都源於理性思考得出的結果 通俗了說就是不會感情用事,事事理性分析然後作為
《博弈聖經》
這個問題很有趣啊,但是看起來這個問題應該歸結於機會成本的概念:選擇A,失去B的機會而所付出的成本。
可以算出來的要利用另一個狗p理論
太有意思了,想多看看這方面的書
嗯嗯 博弈論夫人詭計 也挺好看的。
a+b=c c+c=c c+a=b a=?
a,b,c 都等於0
博弈論是建立在理性人的前提上建立的,即每個人都可以理性的思考自己的處境,並制定相應的策略,給予回應的這個流程。但是現在已經證明瞭,很多時候人得行為都是非理性行為,所以感覺博弈論的理論價值還是遠大於實際價值。
用“納什均衡”來挑戰斯密的“看不見的手”原理,不但是自己無知的表現,也是別有用心的表演!
“納什均衡”的囚徒博弈是一次性博弈,“看不見的手”是無限博弈;“納什均衡”的囚徒博弈是非合作性(非社會性)博弈,而“看不見的手”是合作性(內生社會性)的博弈!
編輯者無知,動不動就挑戰?
是嗎?你有看過國富論的全本嗎
甲乙定合同,乙違約願意支付七萬,甲訴訟可得十萬但交兩萬訴訟費用,該博弈的均衡怎麼求
我來看你設定的這個狀況 從數學上來說,由於甲方訴訟就可取得10萬(純利8萬),所以其實乙方的7萬可以忽略,而甲方的獲利底限即設在 8 萬這條線上。
從題目上來看,若甲乙雙方都不願意再協商,那就直接上法院了
a+b=c c+c=c c+a=b a=?
a+b=c ①;c+c=c ②;c+a=b ③;由②可知:c=0;①代入③得:a+b+a=b⇒a=0
你一句話,俺發了半小時重新整了個,方便大家
耐心
這不屬於博弈論範疇的東西。博弈是由條件限制的,簡化並理論化了社會經濟活動中的一些現象和規律,不是所有。
上課的時候幾次看到過這個博弈理論 但是我不是主修經濟的 看了一個多星期才算是看完了 包括裡面的一些術語 當時看的時候 沒明白經濟人假設是什麼一回事(還是百思不得解啊) 但是好不容易看完的時候 才發現在現實生活要很好的運用博弈論的話 還真的不容易 假設 1,你的對手不按該理論與你競爭怎麼才能贏? 2,你(只是泛指沒有特指,會一點理論或是中等以上,反正不是高手)的對手或伙伴是一個比你強的人,在理論上,你要是用博弈論的話那後果就可想而知了 就像我們經濟學老師說的那樣:他是學經濟的結果炒股還沒朋友(沒學過經濟的)炒得好,一樣
不管怎麼樣人還是不可能完全的做到經濟人的,而且人活得太理性了那就不是自己的想法了,或許就不是自己的最大利益了 不過這個博弈論還是吸引了我 很強大的理論 能讓我從另一個角度來看待事物,角度的不同我可以發現一些沒有過的認識和看法。還是很有意思的一門科學。
以上只是一名博弈論愛好者的學習有感 只是我的一些看法 若有更厲害的人(在博弈論上)希望所加點評 謝謝
很有道理,人不可能做到完全理性
中美貿易戰正好對應貿易戰博弈論
同意
a+b=c c+c=c c+a=b a=?
abc都是0
簡單的設計為付出和利益相關聯之爭,在社會實踐中一些簡化狀態可以參考。









有點深奧!