運籌學
出自 MBA智库百科(https://wiki.mbalib.com/)
運籌學(operations research)，又稱作業研究
目錄 |
運籌學是近代應用數學的一個分支，主要是研究如何將生產、管理等事件中出現的運籌問題加以提煉，然後利用數學方法進行解決的學科。運籌學是應用數學和形式科學的跨領域研究，利用像是統計學、數學模型和演算法等方法，去尋找複雜問題中的最佳或近似最佳的解答。運籌學經常用於解決現實生活中的複雜問題，特別是改善或優化現有系統的效率。
運籌學的思想在古代就已經產生了。但是作為一門數學學科，用純數學的方法來解決最優方法的選擇安排，卻是在二十世紀四十年代才開始興起的一門分支。
運籌學主要研究經濟活動和軍事活動中能用數量來表達的有關策劃、管理方面的問題。當然，隨著客觀實際的發展，運籌學的許多內容已經深入到日常生活當中去了。
隨著科學技術和生產的發展，運籌學已滲入很多領域里，發揮了越來越重要的作用。運籌學本身也在不斷發展，現在已經是包括好幾個分支的數學部門了。
運籌學在英國稱為operational research，在美國稱為operations research，英文縮寫是OR。中國科學工作者取“運籌”一詞作為OR的意譯，包含運用籌劃、以策略取勝等意義。
Operational research（運籌學）一詞最早出現於1938年。當時英國波德塞雷達站負責人A.P.羅提出對整個防空作戰系統的運行研究，以解決雷達站合理配置和整個空軍作戰系統協調配合來有效地防禦德機入侵的問題。1940年9月英國成立了由物理學家P.M.S.布萊克特領導的第一個運籌學小組。後來發展到每一個英軍指揮部都成立運籌學小組。1942年美國和加拿大都相繼建立了運籌學小組。這些運籌學小組在確定護航艦隊的規模、開展反潛艇戰的偵察、組織有效的對敵轟炸等方面作了大量研究，為運籌學有關分支的建立作出了貢獻。
第二次世界大戰後，在這些軍事運籌學小組中工作過的科學家轉向研究在民用部門應用運籌學方法的可能性,從而促進了在民用部門應用運籌學的發展。1947年G.B.丹齊克在研究美國空軍資源配置問題時提出線性規劃及其通用解法──單純形法。50年代初用電子電腦求解線性規劃問題獲得成功。1951年P.M.莫爾斯和G.E.金布爾合著《運籌學方法》一書正式出版，標志著運籌學這一學科已基本形成。到50年代末，美國大企業在經營管理中大量應用運籌學。開始時主要用於制訂生產計劃，後來在物資儲備、資源分配、設備更新、任務分派等方面應用和發展了許多新的方法和模型。60年代中期，運籌學開始用於服務性行業和公用事業。一些發達國家的企業、政府、軍事等部門都擁有相當規模的運籌學研究機構，專門從事有關方法和建模的研究，為決策提供科學的依據。英國在1948年成立了運籌學俱樂部，1954年改名為英國運籌學會，出版《運籌學季刊》。美國在1952年成立了美國運籌學會，出版《運籌學》雜誌。1957年在英國牛津大學召開第一屆國際運籌學會議，以後每隔3年舉行一次。1959年成立國際運籌學聯合會(IFORS)。
中國在1956年曾用過“運用學”的名字，於1957年正式定名為“運籌學”，於1980年成立中國運籌學會（ORSC），並於1982年加入國際運籌學聯合會（IFORS）。
運籌學研究的內容十分廣泛，其主要分支有：線性規劃、非線性規劃、整數規劃、幾何規劃、大型規劃、動態規劃、圖論、網路理論、博弈論、決策論、排隊論、存貯論、搜索論等。
應用運籌學處理問題時分為5個階段。
①規定目標和明確問題：包括把整個問題分解成若幹子問題，確定問題的尺度、有效性度量、可控變數和不可控變數，以及用來表示變數界限和變數間關係的常數和參數。
②收集數據和建立模型：包括定義關係、經驗關係和規範關係。
③求解模型和優化方案：包括確定求解模型的數學方法,程式設計和調試,模擬運行和方案選優。
④檢驗模型和評價解答：包括檢驗模型的一致性、靈敏度、似然性和工作能力，並用試驗數據來評價模型的解。一致性是指主要參數變動時（尤其是變到極值時）模型得出的結果是否合理；靈敏度是指輸入發生微小變化時輸出變化的相對大小是否合適；似然性是指對於真實數據的案例，模型是否適應；工作能力則是指模型是否容易解出，即在規定時間內算出所需的結果。
⑤方案實施和不斷優化：包括應用所得的解解決實際問題，併在方案實施過程中發現新的問題和不斷進行優化。上述5個階段往往需要交叉進行，不斷反覆。
現代運籌學方法強調黑箱方法、數學模型和模擬運行。它重視系統的輸入輸出關係，即問題所處的環境條件和問題中主要因素與環境間的關係，而不追求系統內部機理，因而易於達到從系統整體出發來研究問題的目的。常用的數學模型有：分配模型、運輸模型、選址模型、網路模型、計劃排序模型、存儲模型、排隊模型、概率決策模型、馬爾可夫模型等。模型求解往往成為應用電腦程式進行模擬運行。現在已有各種運籌學軟體包供應，使運籌學可以處理相當複雜的大型問題。隨著運籌學應用於社會大系統，僅靠定量分析已難以找到合理的優化方案，人們常採用定量與定性相結合、在定量分析的基礎上進行定性分析的方法。因此，在許多情況下已很難劃分運籌學、系統分析與政策分析的界限。
運籌學正朝著3個領域發展：運籌學應用、運籌科學和運籌數學。
現代運籌學面臨的新對象是經濟、技術、社會、生態和政治等因素交叉在一起的複雜系統，因此必須註意大系統、註意與系統分析相結合，與未來學相結合，引入一些非數學的方法和理論，採用軟系統的思考方法。總之，運籌學還在不斷發展中，新的思想、觀點和方法不斷出現。
運籌學在經濟管理中的應用實例[1]
運籌學作為一門新興科學，其應用範圍是十分廣泛的。對於不同類型問題，運籌學都有著不同的解決方法，因而形成了許多分支學科。它們雖然各有特性，但在運用系統觀念分析問題，並對問題建立模型求解這兩點上都是共同的。這些分支學科包括線性規劃、非線性規劃、動態規劃、決策分析等等，在此主要介紹線性規劃和動態規劃在經濟管理中的一些應用。
1.線性規劃。
線性規劃是目前在經濟管理中應用最廣泛的一種優化法，它的理論已經十分成熟，可以應用於生產計劃、物資調用、資源優化配置等問題。它主要研究的是經濟管理活動中經常遇到的兩類問題：一類是在有限的勞動力、設備、資金等資源條件下，研究如何合理安排，取得最大的經濟效果（如生產經營利潤）；另一類是為了達到一定的目標（生產指標或其它指標），研究如何組織生產，或合理安排工藝流程，或調整產品的成份等等，以使消耗資料（人力、設備台數、資金原材料等）為最少去實現目標。這類統籌規劃的問題用數學語言表達（即數學模型），先根據問題要達到的目標選取適當的變數，問題的目標通過用變數的函數形式表示(稱為目標函數)，對問題的限制條件用有關變數的等式或不等式表達(稱為約束條件)。當變數連續取值，且目標函數和約束條件均為線性時，稱這類模型為線性規劃的數學模型。下麵舉例說明線性規劃在經濟管理中的應用。
【例1】生產計劃問題(資源配置)。某製藥廠生產甲、乙兩種藥品，生產這兩種藥品要消耗某種維生素。生產每噸藥品所需要的維生素量及所占設備時間見表1。該廠每周所能得到的維生素量為160kg、每周設備最多能開15個台班。且根據市場需求，甲種產品每周產量不應超過4t。已知該廠生產每噸甲、乙兩種產品的利潤分別為5萬元及2萬元。問該廠應如何安排兩種產品的產量才能使每周獲得的利潤最大？
| 每噸產品的消耗 | 每周資源總量 | ||
| 甲 | 乙 | ||
| 維生素/kg | 30 | 20 | 160 |
| 設備/台班 | 5 | 1 | 15 |
解：設該廠每周安排生產甲種藥品的產量為x1(t)，乙種產量為x2(t)，則每周所能獲得的利潤總額為Z = 5x1 + 2x2數學模型為 maxZ = 5x1 + 2x2（目標函數）
用圖解法或單純型方法解略，本題的最優解X * = (2,5),最優值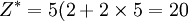
即該廠每周安排生產甲種藥品生產量為2t，乙種產量為5t，每周可獲得最大利潤為20萬元。
2.動態規劃。
動態規劃是運籌學的一個分支，是一種解決多階段決策過程最優化的數學方法，它把困難的多階段的決策問題分解成一系列相互聯繫的較容易解決的單階段決策問題，通過解決這一系列單階段決策問題來解決多階段決策問題。以尋求最優決策序列的方法，動態規劃研究多階段決策過程的總體優化，即從系統總體出發，要求各階段決策所構成的決策序列使目標函數值達到最優。在經濟管理方面，動態規劃可以用來解決最優路徑問題、資源分配問題、生產調度問題、庫存問題、裝載問題、排序問題、設備更新問題、生產過程最優控制問題等等、所以它是現代經濟管理中的一種重要的決策方法。
動態規劃是求解某類問題的一種方法，是考察問題的一種途徑，而不是一種特殊演算法(如線性規劃方法是一種演算法)，現舉例說明動態規劃在經濟管理中的應用。
【例2】庫存-銷售問題。某公司計劃在1月至4月份從事某種商品的經營。已知它的倉庫最多可存儲1000件這種商品，該公司開業時有存貨500件，並根據預測知道，該種商品1月至4月的進價和售價如表2所示。問如何安排進貨量和銷售量，使該公司獲得最大利潤?（假設四月底庫存為零。）
解：若將1月至4月份的購銷安排作為階段k(k=1,2,3,4)，那麼該問題就是一個四階段決策問題。
| 月份(k) | 1 | 2 | 3 | 4 |
| 進價Ck(百元/件) | 10 | 9 | 11 | 15 |
| 售價Pk(百元/件) | 12 | 9 | 13 | 17 |
選擇第k月初公司的存貨量作為狀態變數S_k，第k月的銷售量和進貨量分別作為決策變數U_k和V_k。
狀態轉移方程是
Sk = Sk + Vk − Uk k=1,2,3,4
而
k=1,2,3,4
由已知，S1 = 500；假想有第五價段，S5 = 0。
階段收益函數為rk(Sk;Uk,Vk) = PkUk − CkVk
動態規劃基本方程為
採用逆序法遞推計算（略）
最後得到該問題的最優策略見表3
| 月份 | 月初存貨量S_k(件) | 銷售量U_k(件) | 進貨量V_k(件) |
| 1 | 500 | 500 | 0 |
| 2 | 0 | 0 | 1000 |
| 3 | 1000 | 1000 | 1000 |
| 4 | 1000 | 1000 | 0 |
則該公司獲得的最大利潤為f1(s1) = f1(500) = 16000(百元)=160（萬元）
- ↑ 伍學濱,鄧小英.運籌學在經濟管理中的應用.企業經濟.2005.11
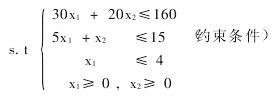
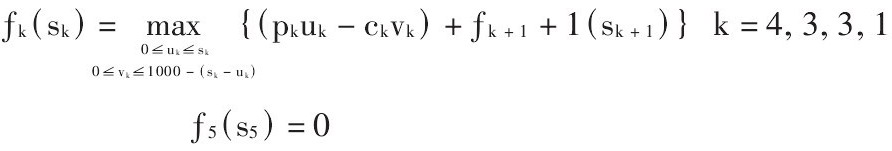
有實例列舉更適合分析