數學規劃
出自 MBA智库百科(https://wiki.mbalib.com/)
- 數學規劃(Mathematical Programming)
目錄 |
什麼是數學規劃[1]
數學規劃是運籌學的一個重要分支，也是現代數學的一門重要學科。其基本思想出現在19世紀初，並由美國哈佛大學的Robert Dorfman於20世紀40年代末提出。數學規劃的研究對象是數值最優化問題，這是一類古老的數學問題。古典的微分法已可以用來解決某些簡單的非線性最優化問題。直到20世紀40年代以後，由於大量實際問題的需要和電子電腦的高速發展，數學規劃才得以迅速發展起來，併成為一門十分活躍的新興學科。今天，數學規劃的應用極為普遍，它的理論和方法已經滲透到自然科學、社會科學和工程技術中。根據問題的性質和處理方法的差異，數學規劃可分成許多不同的分支，如線性規劃、非線性規劃、多目標規劃、動態規劃、參數規劃、組合優化和整數規劃、隨機規劃、模糊規劃、非光滑優化、多層規劃、全局優化、變分不等式與互補問題等。
數學規劃的模型[1]
數學規劃模型的一般形式是：
optf(X)
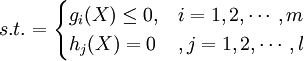
上式中，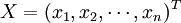
是未知向量，稱為決策變數；f(X)稱為目標函數；gi(X)與hj(X)稱為約束函數。f(X)、gi(X)與hj(X)均為X的數量函數。
符號opt表示對函數f(X)求最優化結果。如果要求f(X)最大，則optf(X)記為maxf(X)。如果要求f(X)最小，則optf(X)記為minf(X)。
符號s.t.為subject to的縮寫，意思是受約束於或受限於m個不等式約束條件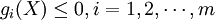
，以及l個等式約束條件
。
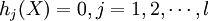於是數學規劃問題可以表述為：求滿足約束條件的x * ，使f(X * )成為最優，而將X * 稱為數學規劃問題的最優解，將f * = f(X * )稱為最優值。
數學規劃的研究[2]
數學規劃論包括豐富和具體的研究方向：線性規劃、非線性規劃、對偶規劃、幾何規劃、整數規劃、動態規劃及多目標規劃等。數學規劃論在社會和經濟的管理和計劃、軍事的指揮和實施、工業產品和系統的設計與運行等諸多領域，有著十分廣泛的應用。
Schmit於1960年提出把數學規劃同有限元方法相結合，使結構優化設計學科的發展正式啟動，逐步形成了結構優化的規劃法分支，後來他同Farshi及以後他又同Fluery等在結構優化設計中的規劃法中吸收了準則法的優點，根據力學特性和工程直覺，他們提出了建立近似顯式模型的近似概念法，包括很多行之有效的措施，如近似顯式逼近、設計變數連接、有效約束粗選、倒數變數的引入、採用對偶求解技術等，使優化效率得到了顯著的改善。許多優化模型因此可以處理成線性規劃問題、二次規劃問題及對偶規劃問題，藉助於數學規劃中成熟的演算法，可以對大多數實際工程問題進行求解。
工程優化問題要求優化演算法具有可靠性、通用性、有效性、健壯性、準確性和方便性，根據這些特性的要求，我們通過對於智能結構最優控制的研究體會到，Schmit等對由結構優化設計建立優化模型和採用優化演算法進行求解所做的工作完全適用於智能結構最優控制的建模與求解。
案例一：生產安排問題[3]
某工廠生產甲、乙兩種產品，生產每件產品需要的原材料、能源消耗、勞動力及所獲利潤見表。
| 品種 | 原材料/kg | 能源消耗/百元 | 勞動力/人 | 利潤/千元 |
| 甲 | 2 | 1 | 4 | 5 |
| 乙 | 3 | 6 | 2 | 6 |
現有庫存原材料1400kg，能源消耗總額不超過2400百元，勞動力滿員為2000人，試安排生產任務(生產甲、乙產品各多少件)，使獲得的利潤最大，並求出最大利潤。
模型建立
設安排生產甲產品x件，乙產品y件，相應的利潤為S，則此問題的數學模型為
maxS = 5x + 6y
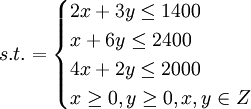
上述數學模型稱為數學規劃模型，其中x、y稱為決策變數，函數S=5x+6y稱為目標函數，這些不等式組構成的限制條件稱為約束條件，記為s.t.。
決策變數、目標函數和約束條件是數學規劃模型的三個要素，若目標函數和約束條件均為線性的數學規劃問題稱為線性規劃，否則稱為非線性規劃。
