多目標規劃法
出自 MBA智库百科(https://wiki.mbalib.com/)
多目標規劃法(multi objective programming approach)
目錄 |
多目標規劃法也是運籌學中的一個重要分支,它是在線性規劃的基礎上,為解決多目標決策問題而發展起來的一種科學管理的數學方法
多目標規劃的概念是 1961年由美國數學家查爾斯和庫柏首先提出的。
多目標規劃是指標準型為:
minZ=CY
s.t AX+Y—Y + = b
X,Y,Y − Y + 1�0
的規劃問題。這裡 C、Y、A、X、Y-、Y + 、b均為矩陣或向量的形式。
與線性規劃相比,多目標規劃標準型的特點在於:
1、偏差列向量 Y − 、Y + 。Y − 、Y + 分別為負、正偏差列向量,各有 m個元素 Y − 、y + 。…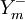 與
與 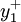
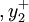 ,…,
,…, (m是約束方程的個數)。負偏差變數的經濟含義為當實際值小於目標值時,實際值與目標值的偏差為負偏差,正偏差變數的經濟含義與之恰恰相反。
(m是約束方程的個數)。負偏差變數的經濟含義為當實際值小於目標值時,實際值與目標值的偏差為負偏差,正偏差變數的經濟含義與之恰恰相反。
2、價值繫數行向量c。c的元素最多不超過 2m個,由目標優先權等級 Pi和目標優先權繫數η組成,即 c = (c1,c2…,c2m)=(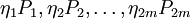 ),在多目標規劃的目標函數中,出現的變數只能是偏差變數。也就是說,列向量 y以正偏差變數和負偏差變數為元素。目標優先權等級 Pi既不是變數,也不是常數,它只是說明不同目標實現的先後順序,這種優先等級的確定一般是由企業決策部門根據企業具體情況及各目標的輕重緩急加以確定的。而目標優先順序繫數,則說明同一優先順序目標相互之間的比例關係。
),在多目標規劃的目標函數中,出現的變數只能是偏差變數。也就是說,列向量 y以正偏差變數和負偏差變數為元素。目標優先權等級 Pi既不是變數,也不是常數,它只是說明不同目標實現的先後順序,這種優先等級的確定一般是由企業決策部門根據企業具體情況及各目標的輕重緩急加以確定的。而目標優先順序繫數,則說明同一優先順序目標相互之間的比例關係。
多目標規劃的解法主要有單純形法和圖解法。圖解法一般只適用於兩個決策變數的情形。單純形法對於求解多目標規劃有普遍意義。
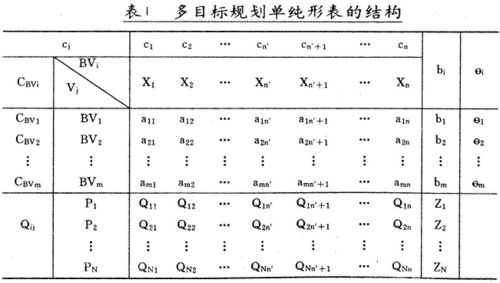
多目標規劃單純形表的結構如表1。
表中 Vj———變數,X1,X2,…,Xn是決策變數,其餘 n-n'個是偏差變數;
Cj———價值繫數,因多目標規劃目標函數不包含決策變數,所以 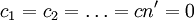 ;
;
bi———目標約束常數;
θi———θ判據;
BVi———基變數名;
CBVi———基變數價值繫數;
aij———作業繫數;
Qij———單純形判據矩陣元素;
Pj———目標優先權排序;
Zj———第 j個優先順序目標的目標函數值。
表1與線性規劃單純形表相比,最大的不同是單純形判據是一個 N×n矩陣,而不是列向量,且有 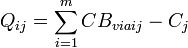 。
。
目標優先權排序 P1,P2,…,PN給出了單純形迭代過程中實現目標的順序。在實現某一優先順序目標後,應依順序考慮一個優先順序能否實現。但是,不能為實現較低目標而使較高級目標的實現受到影響。
多目標規劃的概念是 1961年由美國數學家查爾斯和庫柏首先提出的。至今有些理論問題尚在探討之中,應用範圍還不如線性規劃廣泛。在資源分配、計劃編製、生產調度等方面有一定的’應用。但是,作為一種決策方法,多目標規劃的應用前景還是很樂觀的。企業決策者掌握和運用這種方法將有助於提高管理和決策水平。
某紡織廠生產窗帘布和衣料兩種布料,該廠對這兩種布料的生產能力均是 1000m/h,工廠正常生產能力每周 80h,根據市場預測,下周最大銷售量窗帘布70000m、衣料45000m,窗帘布每米獲利 2.50元,衣料每料獲利 1.50元。該廠定出的經營目標是:
P1:保證生產均衡穩定,避免開工不足;
P2:每周加班時間不超過10h;
P3:努力實現最大銷售量;
P4:儘可能減少加班時間。
本案例多目標規劃模型的決策變數為;x1———周內窗帘布生產的小時數;x2———周內衣料生產的小時數。
每周正常生產能力約束:
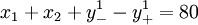
式中 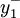 和
和 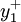 分別表示每周開工低於正常生產能力的負偏差及超出正常生產能力的正偏差。
分別表示每周開工低於正常生產能力的負偏差及超出正常生產能力的正偏差。
銷售目標約束:
x1 + y2 − = 70000 / 1000 = 70
x2 + y3 − = 45000 / 1000 = 45
因產量不能超過最大銷售量,所以 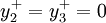
加班時間限制目標約束:
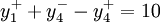
式中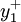 取自每周正常生產能力約束的正偏差,即加班小時數,
取自每周正常生產能力約束的正偏差,即加班小時數,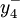 與
與 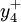 分別表示加班時間不足 10h的負偏差和超過10h的正偏差。
分別表示加班時間不足 10h的負偏差和超過10h的正偏差。
案例二:用多目標規劃法優化企業資本結構[1]
多目標規劃法是運籌學中的數學規劃方法之一。
它是在運籌學基本的數學規劃方法——線性規劃法的基礎上,為了剋服線性規劃方法目標函數單一、約束條件苛刻、無法解決矛盾條件下的規劃問題等缺點而發展起來的規劃方法,使用這種模型能夠解決多種目標同時存在的規劃問題。它以求解實際結果與目標或資源限制之間的偏差變數最小作為目標函數構造的出發點,解決企業生產經營中的各種目標的平衡問題,而被較為廣泛地應用。把目標規劃方法引入資本結構的決策之中,力圖使該決策在考慮企業多個影響因素的條件下進行,也使得決策結果更符合客觀實際。
- 1.資本結構的多目標規劃模型
多目標規劃法的基本數學模型為:
目標函數:
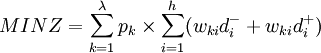
約束條件:
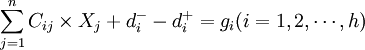
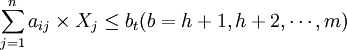
或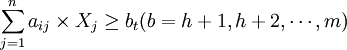
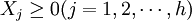
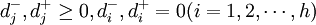
式中:Xj——決策變數;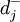 、
、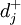 ——正負偏差變數;Cij——第i項目約束條件中Xj的繫數;aij——第t項資源約束條件中Xj的繫數;一般為各項資源的單位消耗定額;gi——第i項目標的既定值;bt——第t項資源約束條件的限制值;Pk——目標的優先順序別;
——正負偏差變數;Cij——第i項目約束條件中Xj的繫數;aij——第t項資源約束條件中Xj的繫數;一般為各項資源的單位消耗定額;gi——第i項目標的既定值;bt——第t項資源約束條件的限制值;Pk——目標的優先順序別;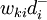 、
、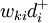 ——第k級優先順序目標中
——第k級優先順序目標中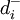 、
、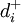 的加權繫數。
的加權繫數。
由於企業資本結構包括資本中的項目構成和各種比例構成,因此,可以將企業的資產負債率和權益與資產總額的比率設為模型中的兩個基本變數vj、vz。再根據涉及企業資本結構的各項指標進行各約束條件的設置。
- 2.資本結構的多目標規劃模型的約束條件設置
企業的經營是在一個非常複雜的大系統中進行的,許多不確定性因素干擾著企業的經濟效益。但是,從影響資本結構決策的角度看,則主要有資金成本、自有資金收益率、企業資本保值增值率、經營風險、獲利能力等因素的影響,因此,其約束環境設置時也主要應考慮以下幾個方面:
- 1)企業預期的資本構成
按照企業資本構成的基本公式:資產=負債+所有者權益,設置出運算的負債總額與自資本總額之和等於企業預期的資產總額的約束。為便於運算,又將其設置為資產負債率和權益與資產總額的比率之和等於1。
- 2)資金成本與自有資金收益率之間相互消長的關係
根據財務杠桿原理,自有資金收益率的大小取決於企業的投資收益率,也取決於資金成本的大小。因此,模型中可設置出在一定的資金成本前提下的自有資金收益率,並使其大於或等於某一期望值的約束條件。
- 3)考慮資本結構給企業經營帶來的風險因素
一般認為,企業的期望收益越大則風險越大。模型中此項約束方程的設置應視不同行業的企業設置風險界限,將風險控制在一定的範圍之內。
- 4)合理的資本結構應使資本的保值增值率大於或等於一定的標準
為保護所有者的利益,財務制度規定企業的資本必須按一定的比率保值增值,在進行資本結構決策時,應結合盈利水平考慮此因素並以一定的下限設置約束。
- 5)企業的獲利能力儘可能達到行業的水平
企業的獲利能力有許多的表示方法,已獲息倍數是其中一個重要的指標,它從盈利與利息之間倍數關係的一定角度上反映了企業的盈利水平。因此,可以某一定值作下限設置出一個約束條件。
根據這些約束條件,建立相應的數學模型,上機求解,即可求出最佳的負債額和資產負債率。
- 3.模型應用
某企業的市場環境不好,經營狀況也不好,總資產報酬率僅為2.08%,平均負債利息率為3.6%。企業現有資產總額為8696.3萬元,本期期望收益額為78萬元。在此前提下,用多目標規劃法確定該企業合理的資本結構。
1)約束條件設置
第1級目標:
根據資產的結構,設資產負債率vj和權益與資產總額的比率vz之和等於1。
即: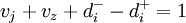 ;
;
第2級目標:
在現有的經營狀態下,若企業能保持78萬元的盈利,則企業的凈資產收益率r不小於0.77%。
式中:e為總資產報酬率
整理得: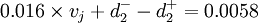 ;
;
第3級目標:
根據企業的盈利能力及經營條件。
企業實現總資產期望報酬率過程中的風險不大於0.1,用標準差F(e)來表示風險。
![F(e)=\left[\sum^n_{t=1}(e_i-e^t)^2\times P_i \right]^{\frac{1}{2}}](/w/images/math/d/9/f/d9f8300abcfca0009011076b0c328d70.png)
根據自有資金收益率與總資產報酬率之間的關係,推導出實現自資金收益率r與風險的關係式,並根據實際情況令其不大於10%。
整理得: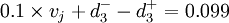 ;
;
第4級目標:
根據財務制度的規定,令資本保值增值率大於105%
因為:![\left[K\times v_z+M\times(1-d)\right]\div K \times v_z \times 100%>105%](/w/images/math/7/e/0/7e0b499c939c86a4e825218c62ca6428.png)
即:![\left[K\times v_z+M\times(1-d)i\right]\div K \times(1-v_j)\times 100%>105%](/w/images/math/7/2/8/728a0539ceacf526f817acae193114be.png)
整理得: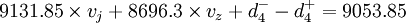
式中:K——企業資產總額;M——企業計劃期的期望收益額。
第5級目標:
企業的已獲息倍數不小於幾年行業的平均水平1.4
因為: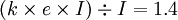
整理得: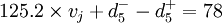
2)構造目標函數根據各約束方程中主要指標的性質,構建出最優資本結構的目標函數模型為:。
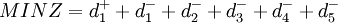
3)上機運算,得到如下結果。
vj = 0.58904 = 59.04%
vz = 0.4096 = 40.96%
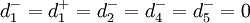 ;
;
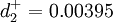
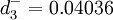
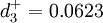
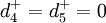
- 4.結論
該企業在考慮各種條件後的資產負債率vj應為59.04%,所有者權益與資產的比率vz應為40.96%。即59%負債和41%所有者權益構成企業合理的資本結構。
- ↑ 劉星 湯亞莉.用多目標規劃法優化企業資本結構.《重慶大學學報(自然科學版)》.2002年7期
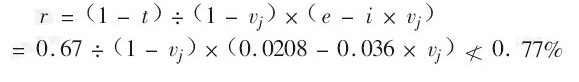
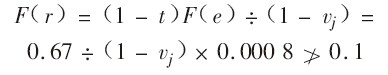








好