線性規劃
出自 MBA智库百科(https://wiki.mbalib.com/)
線性規劃(Linear programming)
目錄 |
線性規劃是運籌學中研究較早、發展較快、應用廣泛、方法較成熟的一個重要分支,它是輔助人們進行科學管理的一種數學方法。在經濟管理、交通運輸、工農業生產等經濟活動中,提高經濟效果是人們不可缺少的要求,而提高經濟效果一般通過兩種途徑:一是技術方面的改進,例如改善生產工藝,使用新設備和新型原材料。二是生產組織與計劃的改進,即合理安排人力物力資源.線性規劃所研究的是:在一定條件下,合理安排人力物力等資源,使經濟效果達到最好。一般地,求線性目標函數線上性約束條件下的最大值或最小值的問題,統稱為線性規劃問題。滿足線性約束條件的解叫做可行解,由所有可行解組成的集合叫做可行域。決策變數、約束條件、目標函數是線性規劃的三要素。
法國數學家 J.- B.- J.傅里葉和 C.瓦萊-普森分別於1832和1911年獨立地提出線性規劃的想法,但未引起註意。
1939年蘇聯數學家Л.В.康托羅維奇在《生產組織與計劃中的數學方法》一書中提出線性規劃問題,也未引起重視。
1947年美國數學家G.B.丹齊克提出線性規劃的一般數學模型和求解線性規劃問題的通用方法──單純形法,為這門學科奠定了基礎。
1947年美國數學家J.von諾伊曼提出對偶理論,開創了線性規劃的許多新的研究領域,擴大了它的應用範圍和解題能力。
1951年美國經濟學家T.C.庫普曼斯把線性規劃應用到經濟領域,為此與康托羅維奇一起獲1975年諾貝爾經濟學獎。
50年代後對線性規划進行大量的理論研究,並涌現出一大批新的演算法。例如,1954年C.萊姆基提出對偶單純形法,1954年S.加斯和T.薩迪等人解決了線性規劃的靈敏度分析和參數規劃問題,1956年A.塔克提出互補鬆弛定理,1960年G.B.丹齊克和P.沃爾夫提出分解演算法等。
線性規劃的研究成果還直接推動了其他數學規劃問題包括整數規劃、隨機規劃和非線性規劃的演算法研究。由於數字電子電腦的發展,出現了許多線性規劃軟體,如MPSX,OPHEIE,UMPIRE等,可以很方便地求解幾千個變數的線性規劃問題。
1979年蘇聯數學家L. G. Khachian提出解線性規劃問題的橢球演算法,並證明它是多項式時間演算法。
1984年美國貝爾電話實驗室的印度數學家N.卡馬卡提出解線性規劃問題的新的多項式時間演算法。用這種方法求解線性規劃問題在變數個數為5000時只要單純形法所用時間的1/50。現已形成線性規劃多項式演算法理論。50年代後線性規劃的應用範圍不斷擴大。 建立線性規劃模型的方法
從實際問題中建立數學模型一般有以下三個步驟:
1.根據影響所要達到目的的因素找到決策變數;
2.由決策變數和所在達到目的之間的函數關係確定目標函數;
3.由決策變數所受的限制條件確定決策變數所要滿足的約束條件。
當我們得到的數學模型的目標函數為線性函數,約束條件為線性等式或不等式時稱此數學模型為線性規劃模型。
例:
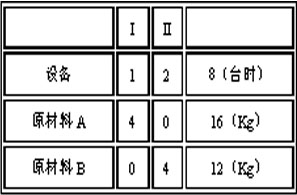
生產安排模型:某工廠要安排生產Ⅰ、Ⅱ兩種產品,已知生產單位產品所需的設備台時及A、B兩種原材料的消耗,如表所示,表中右邊一列是每日設備能力及原材料供應的限量,該工廠生產一單位產品Ⅰ可獲利2元,生產一單位產品Ⅱ可獲利3元,問應如何安排生產,使其獲得最多?
解:
1、確定決策變數:設x1、x2為產品Ⅰ、Ⅱ的生產數量;
2、明確目標函數:獲利最大,即求2x1+3x2最大值;
3、所滿足的約束條件:
設備限制:x1+2x2≤8
原材料A限制:4x1≤16
原材料B限制:4x2≤12
基本要求:x1,x2≥0
用max代替最大值,s.t.(subject to 的簡寫)代替約束條件,則該模型可記為:
max z=2x1+3x2
s.t. x1+2x2≤8
4x1≤16
4x2≤12
x1,x2≥0
求解線性規劃問題的基本方法是單純形法,現在已有單純形法的標準軟體,可在電子電腦上求解約束條件和決策變數數達 10000個以上的線性規劃問題。為了提高解題速度,又有改進單純形法、對偶單純形法、原始對偶方法、分解演算法和各種多項式時間演算法。對於只有兩個變數的簡單的線性規劃問題,也可採用圖解法求解。這種方法僅適用於只有兩個變數的線性規劃問題。它的特點是直觀而易於理解,但實用價值不大。通過圖解法求解可以理解線性規劃的一些基本概念。
可按現代電子電腦標準程式求解線性規劃模型的一般方法。分為代數形式的單純形法和表格形式的單純形法。前者提供基本演算法所依據的邏輯規則,適用於在電子電腦上進行求解運算;後者將變數和數據列成表格,適用於筆算。兩者在數學上是等價的。單純形法是由美國數學家G.B.丹齊克(1914~ )於1947年提出來的,它與蘇聯數學家Л.Β.坎托羅維奇(1912~ )於1938年提出的解乘數法相類似。 根據單純形法的原理,線上性規劃問題中,決策變數(控制變數)x1,x2,…x n的值稱為一個解,滿足所有的約束條件的解稱為可行解。使目標函數達到最大值(或最小值)的可行解稱為最優解。這樣,一個最優解能在整個由約束條件所確定的可行區域內使目標函數達到最大值(或最小值)。求解線性規劃問題的目的就是要找出最優解。
可能出現下列情況之一:①存在著一個最優解;②存在著無窮多個最優解;③不存在最優解,這隻在兩種情況下發生,即沒有可行解或各項約束條件不阻止目標函數的值無限增大(或向負的方向無限增大)。
要縮小對最優解的搜索範圍,就必須認識最優解的一般性質,最優解如果存在的話,則它必然處於可行區域的邊界上。
任何一項約束條件的邊界方程是用“=”號來替換該約束條件中的“≤”或“≥”號而得到的。每一個邊界方程確定一個超平面。因此,可行區域的邊界是由那些滿足一個或同時滿足幾個邊界方程(即處在作為邊界的一個或幾個超平面上)的可行解所組成,而且最優解必在其中。最優解不僅是在可行區域的邊界上,而且也在這個區域的一個隅角上。一個可行解,如果不處在由另兩個可行解連接起來的任何線段上,它就是一個角點可行解。如果連接兩個角點可行解的線段處在可行區域的邊界上,這兩個角點可行解就稱為相鄰的角點可行解。角點可行解具有下列三個重要性質:①如果存在著一個最優解,那麼它必定是角點可行解。如果存在有多個最優解,那麼至少有兩個最優解必定是相鄰的角點可行解。②只存在有限個數的角點可行解。③如果一個角點可行解按目標函數值來衡量時比其所有的相鄰角點可行解更好一些,那它就比所有其他角點可行解都更好,也就是最優解。
上述這些性質構成單純形法的原理基礎。最後一個性質的重要性在於它為一個角點可行解是否是最優解提供了一種簡便的檢驗標準,因而毋需列舉所有的可行解。單純形法正是利用了這個性質,只要檢查少數的角點可行解,並且一旦這個最優性檢驗獲得通過就可立即停止運算。
單純形法的運算步驟可歸結為:①起始步驟──在一個角點可行解上開始。②迭代步驟──移動至一個更好一些的相鄰角點可行解(根據需要反覆進行這一步驟)。③停止法則──在當前角點可行解比所有相鄰角點可行解都更好些時停止。當前角點可行解就是一個最優解。
單純形法的優點及其成功之處在於它只需要較少的有限次數的迭代,即可找到最優解。
在企業的各項管理活動中,例如計劃、生產、運輸、技術等問題,線性規劃是指從各種限制條件的組合中,選擇出最為合理的計算方法,建立線性規劃模型從而求得最佳結果.








線性規劃的基本函數的解,是指的對現有的函數的解,X=sin&+cos2的方程的解不應當是同一樣的解所以每次