排隊論
出自 MBA智库百科(https://wiki.mbalib.com/)
排隊論(Queuing Theory)
目錄 |
研究系統隨機聚散現象和隨機服務系統工作過程的數學理論和方法,又稱隨機服務系統理論,為運籌學的一個分支。
日常生活中存在大量有形和無形的排隊或擁擠現象,如旅客購票排隊,市內電話占線等現象。排隊論的基本思想是1910年丹麥電話工程師A.K.埃爾朗在解決自動電話設計問題時開始形成的,當時稱為話務理論。他在熱力學統計平衡理論的啟發下,成功地建立了電話統計平衡模型,並由此得到一組遞推狀態方程,從而導出著名的埃爾朗電話損失率公式。自20世紀初以來,電話系統的設計一直在應用這個公式。30年代蘇聯數學家А.Я.欣欽把處於統計平衡的電話呼叫流稱為最簡單流。瑞典數學家巴爾姆又引入有限後效流等概念和定義。他們用數學方法深入地分析了電話呼叫的本徵特性,促進了排隊論的研究。50年代初,美國數學家關於生滅過程的研究、英國數學家D.G.肯德爾提出嵌入馬爾可夫鏈理論,以及對排隊隊型的分類方法,為排隊論奠定了理論基礎。在這以後,L.塔卡奇等人又將組合方法引進排隊論,使它更能適應各種類型的排隊問題。70年代以來,人們開始研究排隊網路和複雜排隊問題的漸近解等,成為研究現代排隊論的新趨勢。
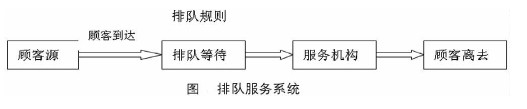
排隊系統又稱服務系統。服務系統由服務機構和服務對象(顧客)構成。服務對象到來的時刻和對他服務的時間(即占用服務系統的時間)都是隨機的。圖1為一最簡單的排隊系統模型。排隊系統包括三個組成部分:輸入過程、排隊規則和服務機構。
輸入過程考察的是顧客到達服務系統的規律。它可以用一定時間內顧客到達數或前後兩個顧客相繼到達的間隔時間來描述,一般分為確定型和隨機型兩種。例如,在生產線上加工的零件按規定的間隔時間依次到達加工地點,定期運行的班車、班機等都屬於確定型輸入。隨機型的輸入是指在時間t內顧客到達數 n(t)服從一定的隨機分佈。如服從泊松分佈,則在時間t內到達n個顧客的概率為
或相繼到達的顧客的間隔時間T 服從負指數分佈,即
式中λ為單位時間顧客期望到達數,稱為平均到達率;1/λ為平均間隔時間。在排隊論中,討論的輸入過程主要是隨機型的。
排隊規則分為等待制、損失制和混合制三種。當顧客到達時,所有服務機構都被占用,則顧客排隊等候,即為等待制。在等待制中,為顧客進行服務的次序可以是先到先服務,或後到先服務,或是隨機服務和有優先權服務(如醫院接待急救病人)。如果顧客來到後看到服務機構沒有空閑立即離去,則為損失制。有些系統因留給顧客排隊等待的空間有限,因此超過所能容納人數的顧客必須離開系統,這種排隊規則就是混合制。
可以是一個或多個服務台。多個服務台可以是平行排列的,也可以是串連排列的。服務時間一般也分成確定型和隨機型兩種。例如,自動沖洗汽車的裝置對每輛汽車沖洗(服務)時間是相同的,因而是確定型的。而隨機型服務時間v 則服從一定的隨機分佈。如果服從負指數分佈,則其分佈函數是
式中μ為平均服務率,1/μ為平均服務時間。
如果按照排隊系統三個組成部分的特征的各種可能情形來分類,則排隊系統可分成無窮多種類型。因此只能按主要特征進行分類。一般是以相繼顧客到達系統的間隔時間分佈、服務時間的分佈和服務台數目為分類標誌。現代常用的分類方法是英國數學家D.G.肯德爾提出的分類方法,即用肯德爾記號 X/Y/Z進行分類。
X處填寫相繼到達間隔時間的分佈;
Y處填寫服務時間分佈;
Z處填寫併列的服務台數目。
各種分佈符號有:M-負指數分佈;D-確定型; Ek-k階埃爾朗分佈;GI-一般相互獨立分佈;G-一般隨機分佈等。這裡k階埃爾朗分佈是指![]() 為相互獨立且服從相同指數分佈的隨機變數時,
為相互獨立且服從相同指數分佈的隨機變數時,![]() 服從自由度為 2k的χ2分佈。例如,M/M/1表示顧客相繼到達的間隔時間為負指數分佈、服務時間為負指數分佈和單個服務台的模型。D/M/C表示顧客按確定的間隔時間到達、服務時間為負指數分佈和C個服務台的模型。至於其他一些特征,如顧客為無限源或有限源等,可在基本分類的基礎上另加說明。
服從自由度為 2k的χ2分佈。例如,M/M/1表示顧客相繼到達的間隔時間為負指數分佈、服務時間為負指數分佈和單個服務台的模型。D/M/C表示顧客按確定的間隔時間到達、服務時間為負指數分佈和C個服務台的模型。至於其他一些特征,如顧客為無限源或有限源等,可在基本分類的基礎上另加說明。
研究排隊系統問題的主要目的是研究其運行效率,考核服務質量,以便據此提出改進措施。通常評價排隊系統優劣有 6項數量指標。
①系統負荷水平ρ :它是衡量服務台在承擔服務和滿足需要方面能力的尺度;
②系統空閑概率P0:系統處於沒有顧客來到要求服務的概率;
③隊長:系統中排隊等待服務和正在服務的顧客總數,其平均值記為LS;
④隊列長:系統中排隊等待服務的顧客數,其平均值記為Lg;
⑤逗留時間:一個顧客在系統中停留時間,包括等待時間和服務時間,其平均值記為WS;
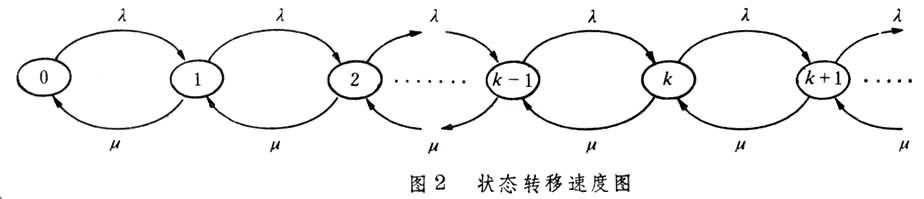
⑥等待時間:一個顧客在系統中排隊等待時間,其平均值記為Wg。M/M/1排隊系統是一種最簡單的排隊系統。系統的各項指標可由圖2中狀態轉移速度圖推算出來(表1)。其他類型的排隊系統的各種指標計算公式則複雜得多,可專門列出計算公式圖表備查。現已開始應用電腦模擬來求解排隊系統問題。
排隊論已廣泛應用於交通系統、港口泊位設計、機器維修、庫存控制和其他服務系統。表2中列出排隊論的應用。
排隊論案例一:超市收銀台[1]
- 一、超市收銀台
隨著市場經濟的不斷發展,城鎮里的超市越來越多。在激烈的市場競爭中,如何提高經營效益、吸引更多的顧客是超市經營商最關心的問題。收銀台是超市的服務視窗,不僅能夠反映超市的形象更與超市的服務質量和經營效率密切相關。收銀員的形象、服務態度、職業技能等固然重要,而收銀台的管理與優化也是不容忽視。顧客選擇超市的標準,不僅是價廉物美的商品,也有服務質量。收銀台前排隊成龍的超市顯然不是人們希望的購物環境,多數人寧願放棄或者稍微走遠一點去購物也不願意在擁擠中排隊等待。尤其是一些成功人士,他們寧願多花點錢也不願意排隊,對於他們來說時間就是金錢。在商品的質量和價格基本相同的條件下,服務質量才是競爭的焦點。前者可以通過採購環節加以控制,而後者只有通過收銀台的增減與管理加以調節。就超市經營者而言,增加收銀台就意味著增加投資,有時還有可能發生資源空閑浪費的現象;而收銀台太少,排隊現象就會嚴重,影響服務質量,造成客源流失。
- 二、超市排隊系統的組成與特征
一般的排隊服務系統(如圖)有三個基本的組成部分:輸入過程、排隊規則和服務機構。輸入過程是指顧客到達排隊系統;排隊規則是指顧客到達後按什麼樣的規則排隊等待服務;服務機構是指為顧客提供服務的機構。本文所研究的排隊系統是指顧客在超市裡挑選好商品後,在收銀台前排隊等待付款的排隊系統。收銀台是服務台,顧客付款被認為是接受服務。輸入過程是指顧客挑選好商品後來到收銀台前;排隊規則是指顧客按單隊單服務台、多隊多服務台或單隊多服務台的方式排隊;服務機構是服務台。
一般認為在超市的排隊系統中,輸入過程服從泊松分佈,服務時間服從指數分佈。用λ表示單位時間內平均到達的顧客數,用μ表示各個服務台的平均服務速率(服務員的服務能力)。用Ρ表示平均每單位時間中系統可以為顧客服務的比例,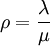 即服務強度。Ws表示顧客在系統中的平均逗留時間(包括排隊等待時間和接受服務的時間),Wq表示顧客排隊等待的平均時間,可通過如下公式計算:
即服務強度。Ws表示顧客在系統中的平均逗留時間(包括排隊等待時間和接受服務的時間),Wq表示顧客排隊等待的平均時間,可通過如下公式計算:
在單隊單服務台的情況下:
 ,
,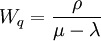
多隊多服務台可看作是多個單隊單服務台。在單隊k個服務台的情況下:
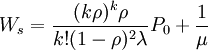 ,
,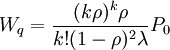

- 三、超市收銀台的優化設計
作為顧客來說,超市收銀台越多越好越方便,而就超市經營者來說,增加收銀台就要增加投資。所以應該合理的規劃收銀台的數量,使得既不會因為收銀台的數量過多而造成資源閑置浪費,也不會因為收銀台的數量過少而造成嚴重的排隊現象。因此可對超市收銀台進行管理和優化設計。
1.對超市佈局進行合理規劃,為顧客營造出溫馨,簡便的購物環境。讓顧客在儘量短的時間內買到自己想買的商品,提高單位時間內進出超市的客流量,這樣既節省了顧客的時間,也使超市增加了顧客的流量,從而使超市的經營效率得到了提高。對於大型的超市在恰當的位置增加導購員是一種很好的方法。對於第一次來消費的顧客,導購員的指導就會大量的減少他們的漫無目的的逗留時間。收銀台前的管理也是非常重要的,儘量讓等待的顧客按順序排隊,避免過分的擁擠和混亂。
2.加強培訓,提高收銀員的基本素質。收銀台是超市中顧客接觸最多的地方。可以說是超市的視窗,收銀員的素質和服務質量直接影響超市的形象。如果超市位於社區內,顧客都是些老客戶,他們知道哪個收銀員的收銀速度比較快,服務態度好,可能就會在她的通道內排隊的顧客比較多,從而導致其他的收銀員暫時的資源閑置。這樣也不利於超市經營者的管理。
所以招收收銀員時要適當考慮收銀員的資歷和形象,要對收銀員的愛崗敬業精神和職業技能加強培訓。要定期對收銀員進行考核或開展職業技能方面的競賽。要及時掌握收銀員的工作狀態、業務水平及相關資料,這不僅是對員工進行科學管理的需要,這些資料可以反映收銀員的工作強度,對於管理與優化都是非常重要的數據資料。
3.儘量採用單隊多服務台的排隊規則,提高工作效率。
在超市排隊系統中,輸入過程服從泊松分佈,從理論來說,採用單隊多服務台的排隊規則比採用多隊多服務台的工作效率高。以有三個收銀台的超市為例,設顧客的平均到達率為λ = 0.9(人),平均服務率為μ = 0.4(人),如果按多隊多服務台的排隊規則進行排隊,則約有75%的顧客需要排隊等待付款,平均等待時間約為7分鐘。而按單隊多服務台的排隊規則進行排隊,則只有約57%的顧客需要排隊,平均等待時間不到2分鐘。
4.誠信經營。在現在的市場經濟條件下,誰占有了消費者的購買信心,誰就占有了市場。所以,超市經營者一定要誠信經營,讓消費者在超市消費時,沒有後顧之憂。使消費者相信他選中的這個超市是可以長期合作的。這樣消費者和經營者就達到了和諧。
排隊論案例二:汽車售後服務[2]
當今排隊論研究的內容包括3個方面:系統的性態、系統的優化和統計推斷,根據資料的合理建立模型,其目的是正確設計和有效運行各個服務系統,使之發揮最佳效益。利用排隊論的知識來解決汽車售後服務中的排隊論問題。
- 1.排隊模型的建立
假設客戶平均到達率為λ,單個服務台的平均服務率(表示單位時間被服務完的顧客數)為μ,整個服務機構的平均服務率為Cμ,系統的服務強度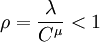 時才不會排成無限的隊列,Pn(c)為C個服務台任意時刻系統中有n個顧客的概率;當到達率為λ,服務率為Cμ的過程達到穩態時,可得
時才不會排成無限的隊列,Pn(c)為C個服務台任意時刻系統中有n個顧客的概率;當到達率為λ,服務率為Cμ的過程達到穩態時,可得
![p_0(c)=\left[ \sum^{c-1}_{k=0}\frac{1}{k!}(\frac{\lambda}{\mu})^k+\frac{1}{c!}\frac{1}{(1-\rho)}(\frac{\lambda}{\mu})^k\right]^{-1}](/w/images/math/4/a/3/4a31b0aee1d72809dce5f405ae5e1c2d.png) (1)
(1)
 (2)
(2)
當系統達到平衡狀態時,每位顧客在系統中的等待時間w的均值為:
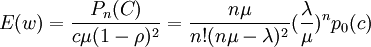 (3)
(3)
排隊逗留的人數:
 (4)
(4)
- 排隊系統的最優化
在排隊系統中,顧客希望服務台越多、服務效率越高、逗留時間越短越好,使自己的損失達到最小,為此4S店就要增加服務人員數,而4S店也不可能無限投入,因此就需要優化設計,目的就是使顧客損失費用和公司運營成本最低。假設服務台的個數為C,每個服務台單位時間所需的成本費為Cs,每個顧客在系統中逗留單位時間的費用為Cw,總成本為Z(c),則目標函數:
minZ(c) = CsC + CwLs
其中Ls為逗留的人數公式(4),C只能取整數。
設C * 是使目標函數C取最小值的點C * 滿足。
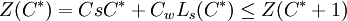
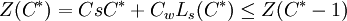 Ls = Ls(C)
Ls = Ls(C)
化簡得: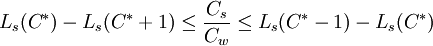 (5)
(5)
通過電腦模擬依次算出LS(1),LS(2),LS(3)…相鄰兩項之差,看常數落在哪兩者之間,從而確定使顧客損失費用和公司服務成本之和達到最優化服務台個數C的最優解C * 。
- 模型的求解
由已知易得:
| λ(輛/h) | μ(輛/h) | Cs(元) | Cw(元) |
| 15.05 | 3.7 | 30.512 | 143.189 |
| LS(1) − LS(2) | -2.7113 | LS(4) − LS(5) | -2.6241 |
| LS(2) − LS(3) | -1.5813 | LS(5) − LS(6) | 0.0203 |
| LS(3) − LS(4) | 1.5020 | LS(6) − LS(7) | 0.0008 |
由上表知只有維修機組個數C * = 4時滿足公式(5),從而使得每一位客戶來店等待維修時間最短,且公司成本最低的最優維修機組個數為4。
模型的分析當顧客平均到達率上升引起服務強度增加致使平均隊長L太大,甚至由於服務強度ρ > 1使隊長趨向無限時,在平均服務率不變的情況下就只能增加服務台。下麵考慮有兩個服務台且平均服務率相等的情況。
兩個服務台的排隊有兩種形式分別由下麵兩圖表示:左圖一個隊是一個M/M/2模型;右圖兩個隊,且入隊後不能換隊,是兩個M/M/1模型。
可以知道,兩個服務台的兩種服務形式平均隊長L,等待時間W之比為: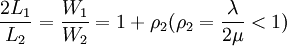
就人們最關心的等待時間而言有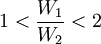 ,而當
,而當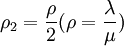 較大時,M/M/2模型的形式比2個M/M/1模型節省較多的等待時間。
較大時,M/M/2模型的形式比2個M/M/1模型節省較多的等待時間。
同理可證:在有多個併列服務台的排隊系統中,排成單隊比排成併列多隊的方案具有明顯的優越性.對於設置多個服務台的隨機過程,應該讓顧客排成一個隊。
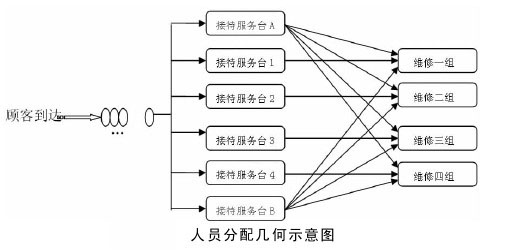
- 接待、派工程式的設計
由上知,在設置4個併列維修機組的排隊系統中,排成單隊比排成併列4隊的方案具有明顯的優越性.具體的接待、派工程式如下:
2.服務月工作安排
在最優條件下,各維修機組基本上一直處於繁忙狀態,但該4S店4月份與9月份來店保養客戶比平均每天來店保養客戶多31%及43%,因此為了在不增加員工數量且遵守國家法定工作時間的條件下完成服務月活動,只能提高各維修機組的工作效率。
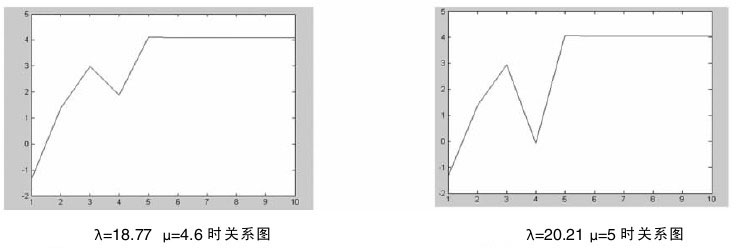
由已知易得:4月份每小時客戶平均到達率λ = 18.77(輛/h),設每個維修機組提高效率後每小時修理的汽車數量為μ,由MATLAB計算得當μ = 4.6時即可滿足條件,此時每個維修機組提高的效率為P=21.8%.同理9月份當μ = 5時即可滿足條件,此時每個維修機組提高的效率P=32.4%。
因此,該4S店的接待、派工流程為圖3,需提高的工作效率如下:
- 各維修機組在4月份、9月份需提高的工作效率
| 時間/月 | λ(輛/時) | μ(輛/時) | P(%) |
| 4 | 18.77 | 4.6 | 21.8 |
| 9 | 20.21 | 5 | 32.4 |
3.結論
應用排隊論一方面可以有效地解決售後服務系統中人員和設備的配置問題,為公司提供可靠的決策依據;另一方面通過系統優化,找出客戶和公司兩者之間的平衡點,既減少排隊等待時間,又不浪費公司人力物力,從而使公司和客戶之間達到雙贏。排隊是一種司空見慣的現象,因此排隊論可以用來解決許多現實問題。
- 徐光輝:《隨機服務系統》,科學出版社,北京,1980。












太複雜啦,應該有一些簡單淺顯的解析嘛