伯特蘭德模型
出自 MBA智库百科(https://wiki.mbalib.com/)
伯特蘭德模型(Bertrand Model)
目錄 |
伯特蘭德模型是由法國經濟學家約瑟夫·伯特蘭德(Joseph Bertrand)於1883年建立的。古諾模型和斯塔克爾伯格模型都是把廠商的產量作為競爭手段,是一種產量競爭模型,而伯特蘭德模型是價格競爭模型,
伯特蘭德模型的假設為:
(2)各寡頭廠商生產的產品是同質的;
(3)寡頭廠商之間也沒有正式或非正式的串謀行為 。
伯特蘭德模型假定,當企業制定其價格時,認為其他企業的價格不會因它的決策而改變,並且n個(為簡化,取n=2)寡頭企業的產品是完全替代品。A、B兩個企業的價格分別為P1、P2 ,邊際成本都等於C。
根據模型的假定,由於A、B兩個企業的產品是完全替代品,所以消費者的選擇就是價格較低的企業的產品;如果A、B的價格相等,則兩個企業平分需求。於是,每一個企業的需求函數為:

因此,兩個企業會競相削價以爭取更多的顧客。當價格降到P1=P2=C時,達到均衡,即伯特蘭德均衡。
結論:只要有一個競爭對手存在,企業的行為就同在完全競爭的市場結構中一樣,價格等於邊際成本。
| 經濟分析工具 |
|---|
| [編輯] |
根據伯特蘭德模型,誰的價格低誰就將贏得整個市場,而誰的價格高誰就將失去整個市場,因此寡頭之間會相互削價,直至價格等於各自的邊際成本為止,即均衡解為:
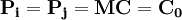
根據伯特蘭德均衡可以得到兩個結論:
2.寡頭的長期經濟利潤為0。
這個結論表明只要市場中企業數目不小於2個,無論實際數目多大都會出現完全競爭的結果,這顯然與實際經驗不符,因此被稱為伯川德悖論
伯特蘭德模型之所以會得出這樣的結論,與它的前提假定有關。從模型的假定看至少存在以下兩方面的問題:
①假定企業沒有生產能力的限制。如果企業的生產能力是有限的,它就無法供應整個市場,價格也不會降到邊際成本的水平上。
②假定企業生產的產品是完全替代品。如果企業生產的產品不完全相同,就可以避免直接的價格競爭。
伯川德模型假設價格為策略性變數而更為現實,但是它所推導出的結果卻過於極端;但由於與現實不甚相符而遭到了很多學者的批評。這是我們為什麼將其稱之為伯川德悖論的主要原因。因此,學者們在研究市場中企業的競爭行為時,更多的是採用古諾模型,即用產量作為企業競爭的決策變數。
伯特蘭德模型的相關案例[1]
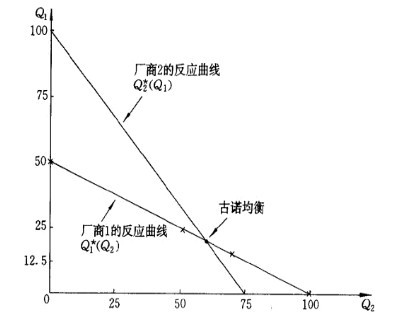
- 圖1 反應曲線與古諾均衡
假設雙寡頭面臨如下一條線性需求曲線:
P=30-Q
其中,Q為兩廠商的總產量,即Q=Q1+Q2。
再假設邊際成本為零,即:
MCl=MC2=0
廠商l的總收益TR1由下式給出:
TR1=PQ1=(30一Q)Ql=30Ql-(Q1)2-Q1Q2
廠商l的邊際收益MR1為:
MRl=30—2Q-Q2
利用利潤最大化條件MRl=MCl=0,得廠商l的反應函數(reaction function)為:
Ql=15—0.5Q2 (1—1)
同理可得廠商2的反應曲線為:
Q2=15-0.5Ql (1—2)
均衡產量水平就是兩個反應曲線交點Q1和Q2的值,即方程組(1—1)式和(1—2)式的解,我們可以求得古諾均衡時的均衡產量水平為:Ql=Q2=10。如圖2所示。
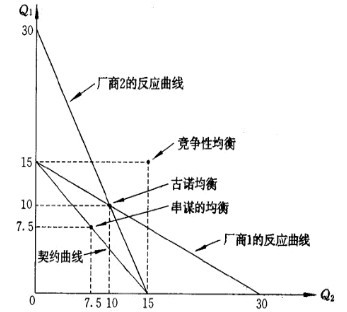
- 圖2 雙寡頭的均衡
因此,在本例中,兩個寡頭的總產量Q為Q1+Q2=20,均衡價格為p=30-Q=10。
剛纔我們討論了兩寡頭廠商相互競爭時的均衡產量。現在我們放寬不能串謀的假設,假定兩寡頭可以串謀,它們能共同確定產量以使總利潤最大化。
這時,兩廠商的總收益TR為:
TR=PQ=(30一Q)Q=30Q—Q2
其邊際收益MR為:
MR=30—2Q
根據利潤最大化條件MR=MC=0,可以求得當Q=15時總利潤最大。如果兩廠商同意平分利潤,每個寡頭廠商將各生產總產量的一半,即Q1=Q2=7.5。其實,任何相加為15的產量Ql和Q2的組合都使總利潤最大化,因此,把Q1+Q2=15稱為契約曲線,而Ql=Q2=7.5是契約曲線上的一個點。如圖2所示。
我們還可以求得當價格等於邊際成本時,Q1=Q2=15,各廠商的利潤為零。
從3個均衡產量可以看到,競爭性均衡時,廠商價格最低,產量最高,利潤為零;串謀均衡時,廠商價格最高,產量最低,利潤最高。
古諾模型和斯塔克爾伯格模型都是把廠商的產量作為競爭手段,是一種產量競爭模型,而伯特蘭德模型是價格競爭模型。在這種模型中,各寡頭廠商通過選擇價格進行競爭,而且各寡頭廠商生產的產品是同質的,寡頭廠商之間也沒有正式或非正式的串謀行為。這一模型是由法國經濟學家約瑟夫·伯特蘭德(Joseph Bertrand)於1883年建立的。現在我們繼續使用上例的數據。設兩個寡頭構成的總市場需求曲線為:
P=30-Q其中Q=Q1+Q2,與上例不同的是,現在兩個廠商有相同的、不為零的邊際成本,譬如:MC1=MC2=3
當兩個寡頭廠商同時選擇產量時,利用上述古諾模型求解均衡產量的方法可以求得古諾均衡是Q1=Q2=9,此時的市場價格為12元,每個廠商均獲利8l元。
不過,現在我們要確定的不是同時選擇產量時的均衡,而是雙方通過同時選擇價格競爭時的均衡狀態。由於產品是同質的,消費者將只會從低價格的廠商處購買。一旦兩個寡頭定價不同,定高價的廠商將不能出售任何產品,而定低價的廠商則占據整個市場。因此這種情況將不會出現,這意味著兩寡頭廠商將定相同的價格,這樣對消費者來說,從哪個廠商購貨都是無差別的。但是,最後具體的價格又是多少呢?現在假設兩個廠商競爭的結果是價格都是高於3元的某個值,那麼在這種情況下,任何一個廠商稍微降價它就將占領整個市場而另一個廠商將喪失所有的客戶;如果兩個廠商競爭的結果是價格都低於3元的某個值,那麼雙方都會虧損。只有當雙方的價格都等於邊際成本3元時(P1=P2=3),雙方再也沒有改變這一價格的動力,此時市場的總產量為27個單位,假如雙方各供給市場一半,即每個廠商都生產13.5個單位,則雙方都沒有利潤。在博弈論中,這種狀態稱為納什(Nash)均衡。這裡的納什均衡也是一種完全競爭的均衡:廠商產量由邊際成本等於邊際收益等於價格來確定,每個廠商的利潤為零。
把伯特蘭德模型的完全競爭均衡狀態與古諾模型的古諾均衡狀態相比可以發現,當把競爭策略選擇變數從古諾模型的產量改為伯特蘭德模型的價格時,每個廠商的產量從9單位增加到13.5單位,價格從12元降低為3元,利潤從81元降為零。
- ↑ 乾春暉主編.管理經濟學.立信會計出版社,2002年06月第1版.
評論(共16條)
“寡頭的長期經濟利潤為0。” 我覺得不對吧? 這種情況應該是短期利潤為0,而長期利潤為-F(也就是固定成本損失)。
期待有瞭解的網友參與貢獻!~~
為什麼要要求企業之間沒有正式或非正式的串謀啊?
這是前提假設
因為不能當經濟利潤為0的時候, 你就不想再降價了,不能虧本吧, 你也敢提高價格, 因為你的競爭對手也在以0利潤出售同樣的商品, 提價你就會失去整個市場, 所以只能是0利潤。
因為當經濟利潤為0的時候, 你就不想再降價了,不能虧本吧, 你也敢提高價格, 因為你的競爭對手也在以0利潤出售同樣的商品, 提價你就會失去整個市場, 所以只能是0利潤。
模型的相關案例 錯了吧~ 那是 Cournot Model 的
說得對,那個確實為古諾的模型
MR=MC,p=ar,p與q間為外生變數關係時(完全競爭價格領袖伯特蘭德)AR=MR,此時p==MC。最後例子有問題








如果有推理公式更好 很有說服力的模型