霍特林模型
出自 MBA智库百科(https://wiki.mbalib.com/)
霍特林模型(Hotelling model)
目錄 |
埃奇沃思模型的說明描述了只有兩個賣者的市場中的不穩定因素。哈羅德·霍特林(Harold Hotelling)在1929年對這一觀點提出挑戰；他認為價格或產出的不穩定並非是寡頭壟斷的基本特征。
霍特林模型簡單來說，就是賣相似產品的店鋪，因為競爭，最後都會開到一起。也可以理解為，在一個理性市場中，兩個競爭者最好的方案，就是做的越來越像。
（1）產品同質；
（2）決策變數：價格；
（3）成本函數相同，且AC＝MC＝C0；
| 經濟分析工具 |
|---|
| [編輯] |
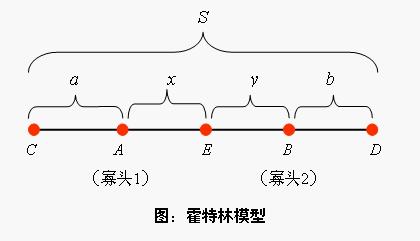
（4）消費者分佈在一條線性的市場上，市場總距離為S公裡，每公裡有一個消費者，每個消費者購買一件商品；
（5）消費者購買商品的交通成本與離商店的距離成比例，單位距離的交通成本為t。
（6）寡頭1的位置位於地點A，寡頭2的位置位於地點B，則：|AC|=a為寡頭1固有的地盤；|BD|=b為寡頭2固有的地盤，|AB|為寡頭1和寡頭2需競爭的地盤，若最終寡頭1爭奪到的地盤為|AE|=x；寡頭2的爭奪到的地盤為|BE|=y如下圖所示，則一定有：
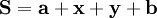
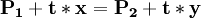
P1，P2分別代表，寡頭1、寡頭2的價格
解以上方程組可得：
;
。
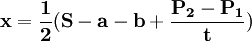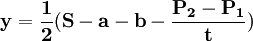1.目標函數：
寡頭1：![\mathbf{\max \pi_1=P_1(a+x)-C_0(a+x)=(P_1-C_0)[a+\frac{1}{2}(S-a-b+\frac{P_2-P_1}{t})]}](/w/images/math/9/5/1/9519e1115f2e34acab20f086e3c22c3f.png)
寡頭2：![\mathbf{\max \pi_2=P_2(b+y)-C_0(b+y)=(P_2-C_0)[b+\frac{1}{2}(S-a-b-\frac{P_2-P_1}{t})]}](/w/images/math/d/f/0/df0536c43207c83d81584d89048a3d55.png)
2.最優決策的一階條件與反應函數
(1)由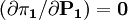
,可得寡頭1的價格反應函數：
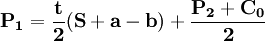
(2)由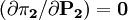
，可得寡頭2的價格反應函數：
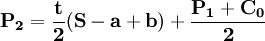
聯立寡頭1和寡頭的價格反應函數，可得：
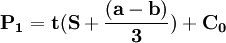
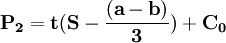
霍特林模型案例[1]
霍特林模型簡單來說，就是賣相似產品的店鋪，因為競爭，最後都會開到一起。也可以理解為，在一個理性市場中，兩個競爭者最好的方案，就是做的越來越像。
比如，我們以A、B兩家店為例，來推導一下博弈的過程。
假設，在一條大約一公裡的街道上，要開AB兩家店，並且兩家店的產品非常相似。
你覺得他們開在哪比較好？
現在有a/b/c三個選項：
a：兩家店分別開在街道兩端。
b：分別開在距離兩端200米的位置。
c：兩家店都在這條街中間開。
你會選哪個？
我們從博弈論的角度來看，選擇開在不同的位置，可能會有怎樣的結果。
第一種情況，假設A和B分別開在了街道兩端，不考慮其他，從距離來看，去兩家店的顧客是均等分佈的。
但這種情況不穩定，為了獲得更多的客戶，可能會有一方先挪動位置。
我們假設，B往左挪動了100米，這樣他能夠輻射的顧客範圍就會更大，自然就會吸引更多顧客來。
A肯定不會眼睜睜看著這種局面發生，你往我這挪100米，那我也往你那挪100米。
一直博弈到最後，可能會出現一種什麼情況呢？
兩家店挨在一起，開在街道中間。
因為只有在這種情況下，才能達到一種均衡。誰也沒法動了，不管往哪移，所能輻射的客戶都會減少。
第二種情況，假設A在距離街道左側100米的地方開了店。
對B來說，他的最優策略是什麼，就是挨著A店，這樣他就能覆蓋右邊900米範圍的人群了。
但是，B這麼做了，A就會往右移，直到兩家經過激烈的競爭，還是會挨在一起開到街道中間。
雖然兩邊的顧客可能會覺得有點不方便，但從博弈的結果來看，這是最合適的，無論誰挪動位置，都不會比這更合適。
- ↑ 為什麼肯德基和麥當勞，總開在一起？.劉潤.2022-03-20
評論(共13條)
T代表什麼？
單位距離的交通成本為t
在"霍特林模型的基本假設"第(5)點，有說明
最優決策的一階條件與反應函數中（1）是對P1求偏導，而不是對P2求偏導。好像版主寫錯了。。。。
謝謝指正，已經做了修改~
P1，P2各指什麼？
是價格，寡1和寡2銷售的物品價格
寡頭2是（P2-C0）吧
沒錯，樓主π2的算式寫錯了 但是後面的計算式是對的
沒錯，樓主π2的算式寫錯了 但是後面的計算式是對的
謝謝指正，已經做了修改~
P1，P2各指什麼？