討價還價模型

出自 MBA智库百科(https://wiki.mbalib.com/)

討價還價模型(Bargain Model)

　　1982年，馬克·魯賓斯坦（Mark Rubinstein）用完全信息動態博弈的方法，對基本的、無限期的完全信息討價還價過程進行了模擬，並據此建立了完全信息輪流出價討價還價模型，也稱為魯賓斯坦模型。

　　魯賓斯坦把討價還價過程視為合作博弈的過程，他以兩個參與人分割一塊蛋糕為例，使這一過程模型化。

　　在這個模型里，兩個參與人分割一塊蛋糕，參與人1先出價，參與人2可以選擇接受或拒絕。如果參與人2接受，則博奕結束，蛋糕按參與人的方案分配；如果參與人2拒絕，他將還價，參與人1可以接受或拒絕；如果參與人1接受，博奕結束，蛋糕按參與人2的方案分配；如果參與人1拒絕，他再出價；如此一直下去，直到一個參與人的出價被另一個參與人接受為止。因此，這屬於一個無限期完美信息博奕，參與人1在時期1，3，5，⋯ 出價，參與人2在時期2，4，6，⋯ 出價。

　　我們用X表示參與人1所得的份額，(1一X)為參與人2所得的份額，X_i和(1 − X_i)分別是時期i時參與人1和參與人2各自所得的份額。假定兩個參與人的貼現因數分別是δ₁和δ₂ 。這樣，如果博奕在時期t結束，參與人1的支付的貼現會值是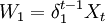，參與人2的支付的貼現值是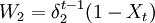。雙方在經過無限期博奕後，可能得到的納什均衡解為：

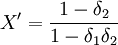　　 （如果）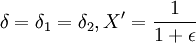

(1)貼現因數

　　貼現因數在數值上可以理解為貼現率，就是1個份額經過一段時間後所等同的現在份額。這個貼現因數不同於金融學或者財務學的貼現率之處在於，它是由參與人的“耐心”程度所決定的。“耐心”實質上是講參與人的心理和經濟承受能力，不同的參與人在談判中的心理承受能力可能各不相同，心理承受能力強的可能最終會獲得更多的便宜；同樣，如果有比其他參與人更強的經濟承受能力，也會占得更多的便宜。

(2)“先動優勢”與“後動優勢”

　　在討價還價的談判中，先出價的一方和後出價的一方有著各自的優勢，即所謂的“先動優勢”和“後動優勢”[41，這兩種優勢的發揮取決於前面提到的耐心優勢。“先動優勢”通過模型可清楚地看出來，為方便起見，假定δ₁ = δ₂ ，當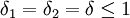，X'=1/1+δ)>0.5。即參與人1的份額總是大於參與人2的份額，始終處於有利的位置，也就是說，在雙方都沒有足夠耐心的情況下，先出價的總是處於有利位置。然而，在雙方都有足夠耐心的情況下，即當δ₁ = δ₂ = δ = 1時，後出價的一方占據了有利位置。這是因為，參與人最後出價時，他將拒絕任何自己不能得到整個份額的出價，一直等到博弈的最後階段得到整個份額為止。這種“後動優勢”只是在理論上有意義，因為現實中的參與人都不可能有足夠的耐心。

(3)“儘快接受”原則

　　由於貼現因數的作用，參與人在本期所得的份額X和下期所得同樣份額的X在價值上是不相等的，下期的x經過貼現只能等於本期的δX，要小於本期的X。因此，參與人均應儘快接受對方合理的報價，否則，即使在下期談判中獲得相同甚至更多的份額也町能小於本期的份額。

　　討價還價模型是以分蛋糕為例來說明利益瓜分問題，企業完全可以利用這個模型進行併購價格的談判活動。

　　首先，我們對討價還價模型做微小的改動，使之能夠適應併購價格談判的應用。原模型是以一塊蛋糕作為整體來考慮的，我們現在把併購中收購方所出的最低價a與被購方所出的最高價b這一區間[a，b]作為整體來考慮。事實上，雙方的價格談判也正是在這一區間上進行的，經過談判，雙方會在價格C處成交，而C一定處在a與b之間。因此，我們可以得到新的模型。

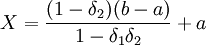　　 （如果δ₁ = δ₂ = δ,）

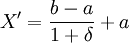　　讓我們看一個具體案例。

　　B公司被A公司收購。經資產評估後，B公司的凈資產為100萬元，B公司根據當時市場狀況及商譽等情況，出價130萬元；A公司則認為B公司的價值只為110萬元，於是還價為110萬元。這裡B公司先出價，A公司後出價。假定雙方貼現因數相同，均為0.9，根據模型，計算出雙方談判的均衡結果為: X'=120.53萬元。

　　這是理想的均衡結果，當然雙方成交價格還存在許多客觀或主觀因素，不一定等於X'，但這個模型還是有很強的實際意義的。