讨价还价模型

出自 MBA智库百科(https://wiki.mbalib.com/)

讨价还价模型(Bargain Model)

　　1982年，马克·鲁宾斯坦（Mark Rubinstein）用完全信息动态博弈的方法，对基本的、无限期的完全信息讨价还价过程进行了模拟，并据此建立了完全信息轮流出价讨价还价模型，也称为鲁宾斯坦模型。

　　鲁宾斯坦把讨价还价过程视为合作博弈的过程，他以两个参与人分割一块蛋糕为例，使这一过程模型化。

　　在这个模型里，两个参与人分割一块蛋糕，参与人1先出价，参与人2可以选择接受或拒绝。如果参与人2接受，则博奕结束，蛋糕按参与人的方案分配；如果参与人2拒绝，他将还价，参与人1可以接受或拒绝；如果参与人1接受，博奕结束，蛋糕按参与人2的方案分配；如果参与人1拒绝，他再出价；如此一直下去，直到一个参与人的出价被另一个参与人接受为止。因此，这属于一个无限期完美信息博奕，参与人1在时期1，3，5，⋯ 出价，参与人2在时期2，4，6，⋯ 出价。

　　我们用X表示参与人1所得的份额，(1一X)为参与人2所得的份额，X_i和(1 − X_i)分别是时期i时参与人1和参与人2各自所得的份额。假定两个参与人的贴现因子分别是δ₁和δ₂ 。这样，如果博奕在时期t结束，参与人1的支付的贴现会值是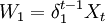，参与人2的支付的贴现值是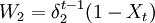。双方在经过无限期博奕后，可能得到的纳什均衡解为：

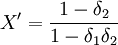　　 （如果）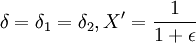

(1)贴现因子

　　贴现因子在数值上可以理解为贴现率，就是1个份额经过一段时间后所等同的现在份额。这个贴现因子不同于金融学或者财务学的贴现率之处在于，它是由参与人的“耐心”程度所决定的。“耐心”实质上是讲参与人的心理和经济承受能力，不同的参与人在谈判中的心理承受能力可能各不相同，心理承受能力强的可能最终会获得更多的便宜；同样，如果有比其他参与人更强的经济承受能力，也会占得更多的便宜。

(2)“先动优势”与“后动优势”

　　在讨价还价的谈判中，先出价的一方和后出价的一方有着各自的优势，即所谓的“先动优势”和“后动优势”[41，这两种优势的发挥取决于前面提到的耐心优势。“先动优势”通过模型可清楚地看出来，为方便起见，假定δ₁ = δ₂ ，当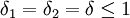，X'=1/1+δ)>0.5。即参与人1的份额总是大于参与人2的份额，始终处于有利的位置，也就是说，在双方都没有足够耐心的情况下，先出价的总是处于有利位置。然而，在双方都有足够耐心的情况下，即当δ₁ = δ₂ = δ = 1时，后出价的一方占据了有利位置。这是因为，参与人最后出价时，他将拒绝任何自己不能得到整个份额的出价，一直等到博弈的最后阶段得到整个份额为止。这种“后动优势”只是在理论上有意义，因为现实中的参与人都不可能有足够的耐心。

(3)“尽快接受”原则

　　由于贴现因子的作用，参与人在本期所得的份额X和下期所得同样份额的X在价值上是不相等的，下期的x经过贴现只能等于本期的δX，要小于本期的X。因此，参与人均应尽快接受对方合理的报价，否则，即使在下期谈判中获得相同甚至更多的份额也町能小于本期的份额。

　　讨价还价模型是以分蛋糕为例来说明利益瓜分问题，企业完全可以利用这个模型进行并购价格的谈判活动。

　　首先，我们对讨价还价模型做微小的改动，使之能够适应并购价格谈判的应用。原模型是以一块蛋糕作为整体来考虑的，我们现在把并购中收购方所出的最低价a与被购方所出的最高价b这一区间[a，b]作为整体来考虑。事实上，双方的价格谈判也正是在这一区间上进行的，经过谈判，双方会在价格C处成交，而C一定处在a与b之间。因此，我们可以得到新的模型。

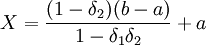　　 （如果δ₁ = δ₂ = δ,）

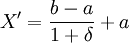　　让我们看一个具体案例。

　　B公司被A公司收购。经资产评估后，B公司的净资产为100万元，B公司根据当时市场状况及商誉等情况，出价130万元；A公司则认为B公司的价值只为110万元，于是还价为110万元。这里B公司先出价，A公司后出价。假定双方贴现因子相同，均为0.9，根据模型，计算出双方谈判的均衡结果为: X'=120.53万元。

　　这是理想的均衡结果，当然双方成交价格还存在许多客观或主观因素，不一定等于X'，但这个模型还是有很强的实际意义的。