方差比率检验
出自 MBA智库百科(https://wiki.mbalib.com/)
| 经济分析工具 |
|---|
| [编辑] |
方差比率检验——新兴资本市场有效的检验方法
一直以来,人们根据市场有效假设来创立现代金融学,随之发展了对市场有效的一些检验方法。其中,证券价格是否随机游走成为市场有效的一个重要判别标准。安德鲁.W.罗(Andrew W. Lo)和艾·克雷格·麦金雷(A.Craig MacKinlay)(1988)提出用方差比率来检验随机游走,之后,该方法得到了普遍的应用。
- 1、市场有效假设
Modigliani和Merton1956年提出在无磨擦市场中资本结构的无关性,Samuelson(1965)标题性提出“Proof that Properly Anticipa-ted Prices Fluctuate Randomly”,至Fama(1970)正式提出有效市场定义,麦克尔(Malkiel)给出了更明确的定义:
在有效市场的下,资产的价格是充分和正确反映了所有相关信息;对所有参与者释放该信息,资产价格不受影响;而且,不能通过有效的信息集合来获取经济利润。Roberts(1967)给信息集分为三类:弱有效、半强有效、强有效。通常,我们所说的市场为弱有效。
在实际中,由于收益是投资机会的一个完全的、不受规模限制的概括,且收益比价格具有更吸引人的统计特征,如平稳性和遍历性,人们更多地使用收益率:
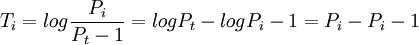
- 2、方差比率检验
Lo和Mackinlay(1988)假定,样本区间内的随机游走增量(RW3)的方差为线性。若股价的自然对数服从随机游走,则方差比率与收益水平成比例。第q期投资水平的方差水平检验统计定义如下:
![VR(q)=Var(lnP_t/lnP_t-q/)/[q \cdot Var(lnP_t/nP_{tl})]](/w/images/math/5/b/1/5b11e05891ffb847a3759251b79b6752.png)
其中,Pt 为t时刻股票价格,Var(·)是其方差的无偏估计。在随机游走假设下,对任何投资水平q,其方差比率VR期望值为1。
Var(lnPt / lnPt − q)和Var(lnPt / lnPt − 1)定义如下:
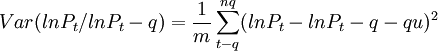
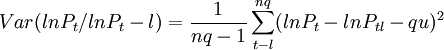
其中,
m = (nq − q + 1)(1 − q / nq)
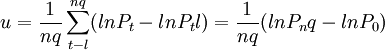
由于金融时间序列常常表现随时间变化的波动性,并且偏离正态分布,Lo和Mackinlay使用的异方差鲁棒性标准正态检验统计量如下:
![Z(q)={[VR(q)-1]^12 \over [\theta(q)]^1/2}\to N(0,1)](/w/images/math/0/7/e/07efd71e237643b02a6c23ad28a32a15.png)
其中,
![[\theta(q)]=\sum_{j-1}^{q-1}[2(q-j)/q]^2\delta(j)](/w/images/math/9/e/6/9e68684bc1e25695f3245cc04e9d2956.png)
![\delta(j)=[\sum_{j-1+1}^{nq}(lnP_t-lnP_t-1-u)^2(lnP_t-j-lnP_t-j-l-u)^2]^2](/w/images/math/0/7/c/07c7a4589bf3ab7ffe9acee79ca52f7f.png)
Lo和Mackinlay(1989)的蒙特卡洛模拟表明,z(q)的渐进分布在有限样本中表现良好,方差比率检验比Dickey-Fuller和Box-Pierce检验更为有效。
- 3、实证检验
80年代以来,全球资本市场得到了很大的发展,对其他一些国家的实证检验相应的纷纷提出,总结如下。
对于欧美成熟市场,Lo和Mackinlay(1988)对美国证券市场 CRSP指数、投资组合、个股分别作了方差比率检验,结果表明:对于指数和组合,RW3假设没有被价值权重指数拒绝;而对于个股,很难发现市场中的可预测部分。1waisako(2003)用1968.01.01——2001.08.15期间东京股票交易所的指数(TOPIX)和按规模排列的组合进行了自相关关系和协自相关关系,得出类似的结论:东京股市指数与组合并不拒绝RW3假设。但Mills(1991、1995)对英国Actuaries All Share Index方差比率检验结果表明英国股票市场拒绝RW3假设。
近来,关于发展中和欠发达等新兴市场弱有效富于争议性。大多数欠发达市场的交易量较小,而在较小的市场中大的交易商更易于操纵市场。尽管一般意义上认为此类新兴市场非有效,如 Cheung等(1993),Classens等(1995),Harvey(1994)和Khababa (1998),然而实证结果并不总是支持这种想法。Branes(1986), Chan等(1992),Dickinson等(1994),以及Ojah等(1999)认为,尽管薄交易问题,发展中和欠发达市场仍然弱有效。
1)亚洲新兴市场
Alam等(1999)用1986.11——1995.12期间的数据检验了孟加拉国、香港、马拉西亚、斯里兰卡和台湾等五个亚洲新兴市场有效性,其方差比率检验结果显示,除斯里兰卡之外,其余市场样本指数序列均服从随机游走。Cheng F.Lee等(2001)对中国股票市场作了检验,其方差比率检验拒绝股票收益服从随机游走假设。Lima等(2004)用1992.06——2000.12期间日收益数据检验了中国(A股、B股)、香港和新加坡三个市场的有效性。除中国B股市场 (上海和深圳)、新加坡市场外,其余市场并不拒绝随机游走假设。
2)拉美新兴市场
Urrutia(1995)使用1975.12——1991.03期间阿根廷、巴西、智利和墨西哥月度指数价格来检验拉美新兴市场证券价格是否服从随机游走假设。其方差比率检验拒绝此假设,而游程检验显示拉美市场弱有效。Grieb和Reyes(1999)使用了圣保罗交易所、墨西哥股票交易所、IFC三个数据库检验巴西和墨西哥股票指数和个股是否服从随机游走。方差比率检验结果显示,墨西哥市场指数和个股、巴西个股均出现均值回复现象,而巴西指数表现出强烈的随机游走趋势。
3)欧洲新兴市场 Graham Smith等(2003)对欧洲希腊、匈牙利、波兰、葡萄牙和土耳其五个新兴市场价格指数作了多元方差比率检验。其中,前四个市场拒绝RW3假设;而土耳其伊斯坦布尔市场在90年代比其他四个市场具有更高的交易量,其股价指数遵从随机游走。
- 4、结论
方差比率检验在各个不同市场中的结果在一定程度上是矛盾的,分析其原因,可能为一下几点:
1) 检验方法本身存在不足
Yoon-Jae Whang等(2003)认为,Lo和Mackinlay(1988)只是集中于检验一段时间内某一时间间隔的方差比率,显然为个体假设检验;Chow和Denning(1993)提出的联合假设检验具有明显的弱点,比如过于守旧、显然的样本失真和真实渐进关键值的低的解释力。因此,应该发展一种新的方法来避免这些不当。
2)市场微观结构的影响
由于各个交易市场的微观结构不同,存在买卖价差、非同期交易等,人为的造成了检验结果上的一些差异。同时,由于各新兴市场规模、流动性不同,以及监管环境的不同,也有可能造成检验结果也趋于不同。
综上,方差比率检验的矛盾性在一定程度上表明,金融资产的收益在某种程度上是可预测的。证券市场微观结构以及交易过程中的摩擦能够形成这种可预测性;因商业条件变化而时刻变化的期望收益也能够形成这种可预测性。同时,资产收益的一定程度上的可预测性对回报投资者所承受的风险是必要的补偿。








我很喜欢