霍特林模型
出自 MBA智库百科(https://wiki.mbalib.com/)
霍特林模型(Hotelling model)
目录 |
埃奇沃思模型的说明描述了只有两个卖者的市场中的不稳定因素。哈罗德·霍特林(Harold Hotelling)在1929年对这一观点提出挑战；他认为价格或产出的不稳定并非是寡头垄断的基本特征。
霍特林模型简单来说，就是卖相似产品的店铺，因为竞争，最后都会开到一起。也可以理解为，在一个理性市场中，两个竞争者最好的方案，就是做的越来越像。
（1）产品同质；
（2）决策变量：价格；
（3）成本函数相同，且AC＝MC＝C0；
| 经济分析工具 |
|---|
| [编辑] |
（4）消费者分布在一条线性的市场上，市场总距离为S公里，每公里有一个消费者，每个消费者购买一件商品；
（5）消费者购买商品的交通成本与离商店的距离成比例，单位距离的交通成本为t。
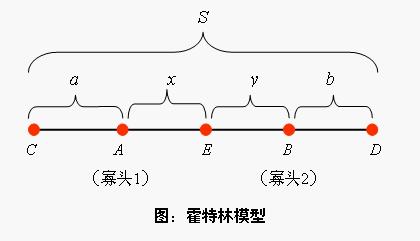
（6）寡头1的位置位于地点A，寡头2的位置位于地点B，则：|AC|=a为寡头1固有的地盘；|BD|=b为寡头2固有的地盘，|AB|为寡头1和寡头2需竞争的地盘，若最终寡头1争夺到的地盘为|AE|=x；寡头2的争夺到的地盘为|BE|=y如下图所示，则一定有：
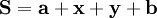
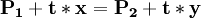
P1，P2分别代表，寡头1、寡头2的价格
解以上方程组可得：
;
。
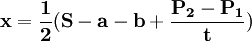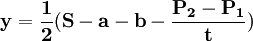1.目标函数：
寡头1：![\mathbf{\max \pi_1=P_1(a+x)-C_0(a+x)=(P_1-C_0)[a+\frac{1}{2}(S-a-b+\frac{P_2-P_1}{t})]}](/w/images/math/9/5/1/9519e1115f2e34acab20f086e3c22c3f.png)
寡头2：![\mathbf{\max \pi_2=P_2(b+y)-C_0(b+y)=(P_2-C_0)[b+\frac{1}{2}(S-a-b-\frac{P_2-P_1}{t})]}](/w/images/math/d/f/0/df0536c43207c83d81584d89048a3d55.png)
2.最优决策的一阶条件与反应函数
(1)由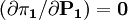
,可得寡头1的价格反应函数：
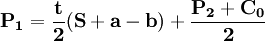
(2)由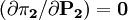
，可得寡头2的价格反应函数：
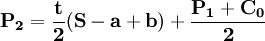
联立寡头1和寡头的价格反应函数，可得：
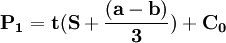
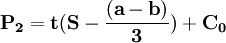
霍特林模型案例[1]
霍特林模型简单来说，就是卖相似产品的店铺，因为竞争，最后都会开到一起。也可以理解为，在一个理性市场中，两个竞争者最好的方案，就是做的越来越像。
比如，我们以A、B两家店为例，来推导一下博弈的过程。
假设，在一条大约一公里的街道上，要开AB两家店，并且两家店的产品非常相似。
你觉得他们开在哪比较好？
现在有a/b/c三个选项：
a：两家店分别开在街道两端。
b：分别开在距离两端200米的位置。
c：两家店都在这条街中间开。
你会选哪个？
我们从博弈论的角度来看，选择开在不同的位置，可能会有怎样的结果。
第一种情况，假设A和B分别开在了街道两端，不考虑其他，从距离来看，去两家店的顾客是均等分布的。
但这种情况不稳定，为了获得更多的客户，可能会有一方先挪动位置。
我们假设，B往左挪动了100米，这样他能够辐射的顾客范围就会更大，自然就会吸引更多顾客来。
A肯定不会眼睁睁看着这种局面发生，你往我这挪100米，那我也往你那挪100米。
一直博弈到最后，可能会出现一种什么情况呢？
两家店挨在一起，开在街道中间。
因为只有在这种情况下，才能达到一种均衡。谁也没法动了，不管往哪移，所能辐射的客户都会减少。
第二种情况，假设A在距离街道左侧100米的地方开了店。
对B来说，他的最优策略是什么，就是挨着A店，这样他就能覆盖右边900米范围的人群了。
但是，B这么做了，A就会往右移，直到两家经过激烈的竞争，还是会挨在一起开到街道中间。
虽然两边的顾客可能会觉得有点不方便，但从博弈的结果来看，这是最合适的，无论谁挪动位置，都不会比这更合适。
- ↑ 为什么肯德基和麦当劳，总开在一起？.刘润.2022-03-20
评论(共13条)
T代表什么？
单位距离的交通成本为t
在"霍特林模型的基本假设"第(5)点，有说明
最优决策的一阶条件与反应函数中（1）是对P1求偏导，而不是对P2求偏导。好像版主写错了。。。。
谢谢指正，已经做了修改~
P1，P2各指什么？
是价格，寡1和寡2销售的物品价格
寡头2是（P2-C0）吧
没错，楼主π2的算式写错了 但是后面的计算式是对的
没错，楼主π2的算式写错了 但是后面的计算式是对的
谢谢指正，已经做了修改~
P1，P2各指什么？