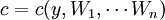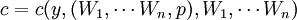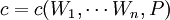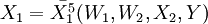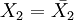成本函数

出自 MBA智库百科(https://wiki.mbalib.com/)

成本函数（Cost Function）

　　成本函数（Cost Function）是指在技术水平和要素价格不变的条件下，成本与产出之间的相互关系。成本理论主要分析成本函数。

　　成本函数和成本方程不同，成本函数说的是成本和产量之间的关系，成本方程说的是成本等于投入要素价格的总和，如果投入的是劳动L和资本K，其价格为PL和PK，则成本方程是C=L·PL+K·PK，成本方程是一个恒等式，而成本函数则是一个变量为产量的函数式。

　　短期成本函数反映了在技术、规模、要素价格给定条件下，最低成本随着产量变动而变动的一般规律。技术水平是通过生产函数来刻划的。因此，成本函数和生产函数之间存在着非常密切的关系。若给定生产函数和要素价格，就可以推导出成本函数。

• c = c(y)

　　第一种定义形式为多数初中级教材和部分文献采用。在该函数中，产出水平是唯一变量。该种定义形式表明成本随产出水平的变化而变化。与其它因素无关，显然没有反映出厂商的生产决策过程，同时与可观测的厂商行为不符，不是一个定义良好的函数。如为方便和易于教授，则在授课过程中应明确告知学生该种定义形式并不是真正意义上的厂商的成本函数，同时文献的读者也应对此问题加以注意。

　　第二种定义形式，正确反映的厂商的生产决策过程，提供了对该函数的可据以证伪的实。然而该函数从形式上看，赋予产出平和要素价格同等的变量地位，掩盖了产出水平事实上是既定参数而要素价格足真正意义上的变量。从而未能正确揭示厂商的生产决策过程。

　　第三种定义形式，成本函数在形式上明确指出产出水平是要价格和产品价格的函数．同时，成本是要素价格的函数。从而产出水平是成本和要素价格的中间变量。揭示了厂商的决策过程，依琚要素价格和产品价格确定相应的产出水平，在该产出水平下，依据要素价格确定要素的使用量从而使成本最小化。

　　第四种定义形式从本质上指出成本的真正决定因素或成本函数的真正变量是要素价格和产品价格。产出水平虽然是厂商决策的中间过程变量，并不在最根本的意义上影响成本。但却足厂商决策过程必不可少的，因而该种定义未能反映厂商的生产决策过程。

　　1.是W的非减函数。对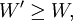

　　2.是W的一次其次函数：对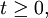

c(tW,y) = tc(W,y)

　　3.是W的凹函数：对

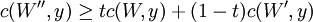
　　4.当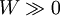时，是W的连续函数。（当很好的定义时）

• 短期成本函数

　　短期成本函数指反映在企业诸种投入要素中至少有一种要素的投入量固定不变的条件下产量与成本之间关系的数学函数。

　　短期生产函数和短期成本函数之间的对应关系表现为：边际报酬递增阶段对应的是边际成本递减阶段，边际报酬递减阶段对应的是边际成本递增阶段，与边际报酬极大值对应的是边际成本极小值。

　　短期成本函数：只有可变要素可以调整的情况下，生产既定产量时的最小成本与产量的关系。假定要素2短期是固定的，则该函数为：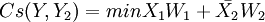

　　使得：

• f(X₁,X₂) = Y

　　因此，在短期内，生产产量为Y的最小成本取决于不变要素的投入量和要素的价格。

求得

　　即：在短期内，在任何既定价格和产量下，变动要素的投入量取决于固定要素的投入量

　　即最小成本就是与成本最小化的要素选择有关的成本。

• 长期成本函数

　　长期成本函数是由ｎ个短期成本函数综合而成的。如果说短期成本函数表示在一个特定的生产规模下生产各种产量水平所耗费的最小的成本，那么，长期成本函数表示在ｎ个可供选择的生产规模下生产各种产量水平所耗费的最小的成本。

　　长期成本函数：表示在一切生产要素都可以自由调整的情况下，生产既定产量时的最小成本和产量的关系。 该函数表示为： Cs(Y) = minX₁W₁ + X₂W₂；使得:f(X₁,X₂) = Y；由于两种要素都可以变动，长期成本仅与既定要素价格下的产量有关。

　　求得：

• X₁ = X₁(W₁,W₂,Y)； X₂ = X₂(W₁,W₂,Y)

• C(Y) = W₁X₁(W₁,W₂,Y) + W₂X₂(W₁,W₂,Y)

　　最小成本就是厂商利用成本最小化的要素选择所产生的成本

　　长期成本函数是规划中的成本函数。