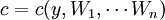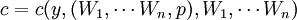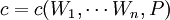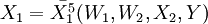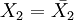成本函數

出自 MBA智库百科(https://wiki.mbalib.com/)

成本函數（Cost Function）

　　成本函數（Cost Function）是指在技術水平和要素價格不變的條件下，成本與產出之間的相互關係。成本理論主要分析成本函數。

　　成本函數和成本方程不同，成本函數說的是成本和產量之間的關係，成本方程說的是成本等於投入要素價格的總和，如果投入的是勞動L和資本K，其價格為PL和PK，則成本方程是C=L·PL+K·PK，成本方程是一個恆等式，而成本函數則是一個變數為產量的函數式。

　　短期成本函數反映了在技術、規模、要素價格給定條件下，最低成本隨著產量變動而變動的一般規律。技術水平是通過生產函數來刻劃的。因此，成本函數和生產函數之間存在著非常密切的關係。若給定生產函數和要素價格，就可以推導出成本函數。

• c = c(y)

　　第一種定義形式為多數初中級教材和部分文獻採用。在該函數中，產出水平是唯一變數。該種定義形式表明成本隨產出水平的變化而變化。與其它因素無關，顯然沒有反映出廠商的生產決策過程，同時與可觀測的廠商行為不符，不是一個定義良好的函數。如為方便和易於教授，則在授課過程中應明確告知學生該種定義形式並不是真正意義上的廠商的成本函數，同時文獻的讀者也應對此問題加以註意。

　　第二種定義形式，正確反映的廠商的生產決策過程，提供了對該函數的可據以證偽的實。然而該函數從形式上看，賦予產出平和要素價格同等的變數地位，掩蓋了產出水平事實上是既定參數而要素價格足真正意義上的變數。從而未能正確揭示廠商的生產決策過程。

　　第三種定義形式，成本函數在形式上明確指出產出水平是要價格和產品價格的函數．同時，成本是要素價格的函數。從而產出水平是成本和要素價格的中間變數。揭示了廠商的決策過程，依琚要素價格和產品價格確定相應的產出水平，在該產出水平下，依據要素價格確定要素的使用量從而使成本最小化。

　　第四種定義形式從本質上指出成本的真正決定因素或成本函數的真正變數是要素價格和產品價格。產出水平雖然是廠商決策的中間過程變數，並不在最根本的意義上影響成本。但卻足廠商決策過程必不可少的，因而該種定義未能反映廠商的生產決策過程。

　　1.是W的非減函數。對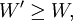

　　2.是W的一次其次函數：對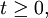

c(tW,y) = tc(W,y)

　　3.是W的凹函數：對

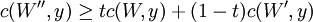
　　4.當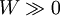時，是W的連續函數。（當很好的定義時）

• 短期成本函數

　　短期成本函數指反映在企業諸種投入要素中至少有一種要素的投入量固定不變的條件下產量與成本之間關係的數學函數。

　　短期生產函數和短期成本函數之間的對應關係表現為：邊際報酬遞增階段對應的是邊際成本遞減階段，邊際報酬遞減階段對應的是邊際成本遞增階段，與邊際報酬極大值對應的是邊際成本極小值。

　　短期成本函數：只有可變要素可以調整的情況下，生產既定產量時的最小成本與產量的關係。假定要素2短期是固定的，則該函數為：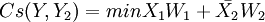

　　使得：

• f(X₁,X₂) = Y

　　因此，在短期內，生產產量為Y的最小成本取決於不變要素的投入量和要素的價格。

求得

　　即：在短期內，在任何既定價格和產量下，變動要素的投入量取決於固定要素的投入量

　　即最小成本就是與成本最小化的要素選擇有關的成本。

• 長期成本函數

　　長期成本函數是由ｎ個短期成本函數綜合而成的。如果說短期成本函數表示在一個特定的生產規模下生產各種產量水平所耗費的最小的成本，那麼，長期成本函數表示在ｎ個可供選擇的生產規模下生產各種產量水平所耗費的最小的成本。

　　長期成本函數：表示在一切生產要素都可以自由調整的情況下，生產既定產量時的最小成本和產量的關係。 該函數表示為： Cs(Y) = minX₁W₁ + X₂W₂；使得:f(X₁,X₂) = Y；由於兩種要素都可以變動，長期成本僅與既定要素價格下的產量有關。

　　求得：

• X₁ = X₁(W₁,W₂,Y)； X₂ = X₂(W₁,W₂,Y)

• C(Y) = W₁X₁(W₁,W₂,Y) + W₂X₂(W₁,W₂,Y)

　　最小成本就是廠商利用成本最小化的要素選擇所產生的成本

　　長期成本函數是規劃中的成本函數。