短期生產函數
出自 MBA智库百科(https://wiki.mbalib.com/)
短期生產函數(short-run production function )
目錄 |
什麼是短期生產函數[1]
短期生產函數是指在短期內至少有一種投入要素使用量不能改變的生產函數。在短期內,假設資本數量不變,只有勞動可隨產量變化,則生產函數可表示為Q=f(L),這種生產函數可稱為短期生產函數。微觀經濟學通常以一種可變生產要素的生產函數考察短期生產理論,以兩種可變生產要素的生產函數考察長期生產理論。
短期生產函數相關概念[2]
為了探討短期生產規律,需要從總產量、平均產量和邊際產量這三個概念及相互關係說起。
假定生產某種產品需要兩種投入要素:資本K和勞動L,其中資本K為固定投入要素,勞動L是可變投入要素。產量隨著勞動者人數的變化而變化。下麵,我們引入總產量、平均產量和邊際產量三個概念來說明產量和勞動之間的關係。
勞動的總產量(total product,TPL)指短期內在技術水平既定條件下,利用一定數量的可變要素(如勞動)所生產產品的全部產量。其表達式為:TPL=f(L)。
勞動的平均產量(average product,APL)是指平均每一單位可變要素所分攤的總產量。其表達式為:
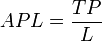
勞動的邊際產量(marginal product,MPL)是指增加一單位可變要素的投入所導致的總產苗量的增加量。其表達式為:
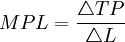
或
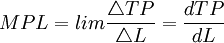
我們利用表1來說明這三個概念及其關係。表1描述了某服裝公司的生產情況。對於生產服裝的企業來說,其擁有的機器設備和廠房在短期內是固定的,但是所雇用的操作縫衣機器設備的勞動力是可以調整的,工廠的管理人員必鬚根據銷售情況作出雇用多少工人的決策。表1給出了該服裝公司勞動的投入與產出之間的關係。第二列表示資本固定不變,第三列表示與不同勞動投入所對應的總產出量。隨著勞動投入量的增加,總產出在逐漸增加,當勞動投入達到6個單位時,總產出達到最大值,再增加一個單位勞動,勞動投入達到7個單位時,總產出沒有發生變化。當投入的勞動繼續增加時,總產出反而開始減少。
| 可變投入量 (L) | 固定投入量 (K) | 總變數 (TPL) | 平均產量 (APL) | 邊際產量 (MPL) |
| 0 | 10 | 0 | ||
| 1 | 10 | 3 | 3 | 3 |
| 2 | 10 | 10 | 5 | 7 |
| 3 | 10 | 24 | 8 | 14 |
| 4 | 10 | 36 | 9 | 12 |
| 5 | 10 | 40 | 8 | 4 |
| 6 | 10 | 42 | 7 | 2 |
| 7 | 10 | 42 | 6 | 0 |
| 8 | 10 | 40 | 5 | -2 |
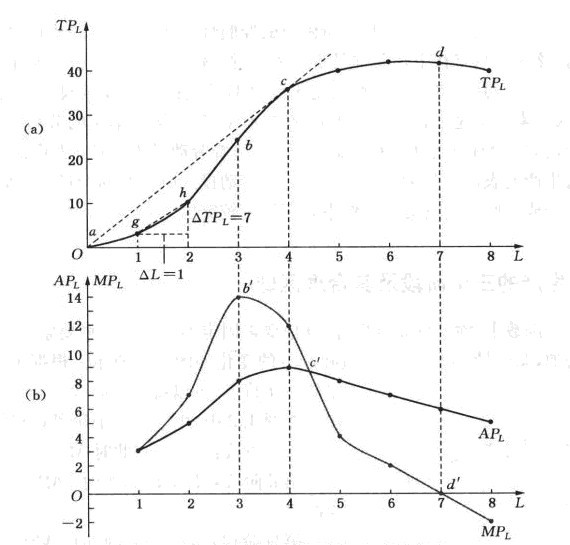
利用表1中的數據可以繪製成圖1。在圖1中,橫軸表示勞動投入量,縱軸表示產出量。圖1(a)中TPL表示總產量曲線,從圖中我們可以看出,服裝公司的總產量伴隨勞動投入從零開始逐漸增加,總產量曲線TPL先以遞增的速度增加,到達拐點b以後,增速開始減慢,到達點d時總產量到達最大值,過點d後總產量則變為遞減。圖1(b)中的APL和MPL分別表示平均產量曲線和邊際產量曲線。從圖中可以看出,服裝公司的平均產量先隨勞動投入的增加而增加,達到最高點c'後即不斷下降。而邊際產量從幾何意義上看即為總產量曲線上其相對應的某點的斜率。根據總產量曲線的特點,在總產量到達拐點之前,其切線的斜率為正且遞增,過拐點之後,切線的斜率雖為正但呈遞減,達最高點之後,切線的斜率即為負。因此,與總產量相對應的邊際產量MPL起先可能有短暫的上升,到達點b'後其即不斷下降,過了點d'後MPL變為負數。
從表1和圖1中,我們可以看出,隨著可變投入使用量的不斷增加,邊際產量最終可能變為負值。比如,當企業每天雇用8個工人時,工作場所會變得十分擁擠,勞動者在做工作的時候會相互礙事。因此,如果增雇第8個工人,總產量實際上會減少,所以,邊際產量變為負值。這就是所謂“人多反而誤事”的現象。
圖1 一種可變要素的投入與產量之間的關係
綜上所述,我們可以對各種產量曲線相互間的關係歸納如下:
(1)當TP曲線上升時,MP為正;TP下降時,MP為負;因此,當TP為極大時,MP=0。
(2)當MP>AP時,AP曲線上升;MP<AP時,AP曲線下降,MP曲線通過AP曲線的最高點,此時MP=AP。
為了更清楚地說明AP與MP的關係,我們不妨找一實例來說明。設有某一班級學生的平均身高為160釐米(相當於AP),若轉入一位新同學,其身高為170釐米(相當於MP),即原先全班的平均身高小於轉入者(即AP小於MP),這樣就會由於轉入者的身高的“拉動”,使得後來全班的平均身高增加(相當於AP呈遞增)了;反之若班上轉入一位新同學,其身高為150釐米(相當於MP),比原班上的身高小時(MP<AP),則該班上新的平均身高會下降(即AP此時呈遞減)。這個例子比較形象地說明瞭平均產量和邊際產量的關係。
在上述服裝公司的例子中,隨著雇用工人的增加,當增加更多的工人時,每增加1個工人所帶來的總產量的增量會越來越小。比如,該服裝公司的邊際產量在第4個工人之後開始遞減,囂一直到第7個工人的邊際產量為零。這一邊際產量連續下降的過程被稱為邊際報酬遞減規律。號該規律表述如下:邊際報酬遞減規律(1aw of diminishing return)是指在其他條件不變時,連續將生某一生產要素的投入量增加到一定的數量之後,總產量的增量即邊際產量將會出現遞減現象。
一般認為,邊際報酬遞減規律並不是根據經濟學中的某種理論或原理推導出來的規律,它只是根據對實際的生產和技術情況觀察所做出的經驗性的概括,反映了生產過程中的一種純技術關係。同時,該規律只有在下述條件具備時才會發生作用:(1)生產技術水平既定不變;(2)除一種投入要素可變外,其他投入要素均固定不變;(3)可變的生產要素投入量必須超過一定點。也就是說,投入要素不是完全替代品。比如,在農業生產中,第一單位的勞動與一些農業機械及一塊耕地結合時,開始有可能明顯增加總產量,但隨著勞動投入增加,過了某一點之後,下一單位勞動投入所生產的農產品數量將小於前一單位勞動投入所生產的產量。因此,邊際報酬遞減規律在農業生產或一些勞動密集型工作中表現得比較突出。
在短期生產函數中,除一種要素以外,其他要素固定不變。在一種要素可變情況下,隨著可變要素逐漸增加,總產量、平均產量及邊際產量的變化如圖2所示。
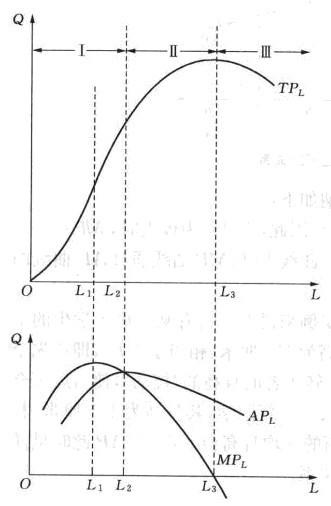
圖2 生產的三個階段
根據平均產量及邊際產的變化特點,可以將生產或者要素的投入分為三個階段。在圖2中,生產的三個階段具有如下特點:
第I階段:(0,L2),此時MPL>APL,APL遞增。
第Ⅱ階段:(L2,L3),此時,APL>MPL>0,APL遞減。
第Ⅲ階段:(L3,∞),此時,MPL<0時,TPL呈遞減。
在第I階段中,可變要素的投入量從0增加到L2個單位時,在這階段各種產量曲線的變化特征為:勞動的平均產量始終是上升的,並且達到最大值;勞動的邊際產量達到最大值後開始遞減,但其始終大於勞動的平均產量;勞動的總產量始終是增加的。所以,此階段稱為平均產量遞增階段。這說明在本階段,固定要素投入相對過多,增加可變要素的投入有利於兩者搭配比例更加合理化。因此,第I階段可稱為生產力尚未充分發揮的階段,在該階段理性廠商對可變要素的投入不會停止。
在第Ⅱ階段中,AP雖開始下降,但仍相當高;同時MP>0,這時繼續投入生產要素,仍會有額外的產出。因此,第2階段可稱生產的經濟階段。亦可稱為生產的合理區域。
在第Ⅲ階段中,MP<0,TP開始下降,這表示生產要素投入過多,不但不能增加生產,反而使總產量減少,使生產者蒙受雙重損失,一是資源的浪費,二是總產量的減少。因此,第Ⅲ階段可稱為生產不經濟的階段。
綜合以上所述,可知第I階段中要素的生產力尚未充分發揮,不是最有利的生產階段。第Ⅲ階段中要素的邊際產量為負,總產量開始下降,此種情形不但無利,而且有害,因此也不是有利的生產階段。第Ⅱ階段則無上述兩階段的缺點,故為生產的經濟階段。至於廠商在實際生產中會選取第Ⅱ階段中的哪一點來安排生產,要看生產要素的價格,如果相對於資本的價格而言,勞動的價格較高,則勞動的投入量靠近點L2對於生產者較有利;若相對於資本的價格而言,勞動的價格較低,則勞動的投入量靠近點L3對於生產者較有利。無論如何,都不能將生產維持在第I階段或推進到第Ⅲ階段。
短期生產函數案例[2]
已知某企業的生產函數為Q=21L+9L2-L3,求:
(1)該企業的平均產出函數和邊際產出函數。
(2)如果企業現在使用了3個勞動力,試問是否合理?如果不合理,那合理的勞動使用量應在什麼範圍內?
(3)如果該企業的產品的市場價格為3元,勞動力的市場價格為63元。那麼,該企業的最優勞動投入量是多少?
【解】
(1)平均產出函數為:APL=Q/L=21+9L-L2。
邊際產出函數為:MPL=21+18L-3L2。
(2)我們首先確定合理投人區間的左端點。令AP=MP,即:
21+9L-L2=21+18L一3L2
整理,得
2L2-9L==0
可解得L=0(捨去)與L=4.5。所以,合理區間的左端點應在勞動力投人為4.5的時候。
再定合理區域的右端點。令MP=0,即:
21+18L-3L2=0
整理,得
L2-6L-7=0
解得:L=-1(捨去)與L=7。
所以,合理區域的右端點為L=7。
這樣合理區域為4.5≤L≤7。
目前的使用量L=3,所以是不合理的。
(3)勞動投入最優的必要條件為P·MPL=w。所以,
(2l+18L-3L2)3=63
容易解出:L=0(捨去)或L=6。
因此,L=6,即使用6個勞動力為該企業的最優勞動投入量。
評論(共4條)
根據定義,邊際產量等於每增一單位的勞動要素所改變的產量(ΔQ/ΔL),這個結果並不是生產函數的導數dy/dx(lim△L→0 ΔQ/ΔL ),畫圖的時候是按照定義畫的,下麵案例做題是根據導數做的,怎麼解釋呢?
邊際產出函數為:MPL=21+18L-3L2。為什麼我算出來的邊際函數是MPL=21+18L-7L²
求導數求錯了。








非常好!