ELES模型
出自 MBA智库百科(https://wiki.mbalib.com/)
ELES模型(Extend Linear Expenditure System,擴展線性支出系統模型)
目錄 |
擴展線性支出系統模型(Extend Linear Expenditure System,ELES)是經濟學家Luch於1973年在美國經濟計量經濟學家Stone的線性支出系統模型的基礎上推出的一種需求函數系統。
該系統假定某一時期人們對各種商品(服務)的需求量取決於人們的收入和各種商品的價格,而且人們對各種商品的需求分為基本需求和超過基本需求之外的需求兩部分,並且認為基本需求與收入水平無關,居民在基本需求得到滿足之後才將剩餘收入按照某種邊際消費傾向安排各種非基本消費支出。
假設將人們的消費支出具體劃分為I類,則各類商品的消費支出可以用模型表示為:
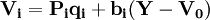 (1)
(1)
| 經濟分析工具 |
|---|
| [編輯] |
其中,
- Vi是對第I類商品的消費支出,
- Pi和qi分別為第I類商品的價格和基本需求量,
- bi為邊際消費傾向,
- V0為基本需求總支出,
- Y為收入水平。
該模型即為“擴展線性支出系統模型”(ELES模型)。
如果樣本數據為橫截面數據,則可以設:
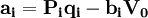 (2)
(2)
則模型(1)可以表示為:
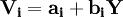 (3)
(3)
對公式(2)兩端求和得:
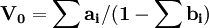 (4)
(4)
由公式(2)也可以得出:
 (5)
(5)
在消費結構分析中,目前通常採用的是恩格爾函數(Engel function)和擴展線性支出系統(Extended Liner Expenditure System , 簡稱ELES)模型,二者在形式和內涵上都有非常密切的聯繫。ELES模型的突出優點在於:它考慮了收入和價格因素對居民消費結構的影響,把居民的各項消費支出看作是相互聯繫、相互制約的行為,在沒有價格資料的情況下,也能根據截面數據資料估計出各種商品的基本需求支出,進行需求結構估算,可以計算出收入彈性,進行需求彈性分析。
1947年,L.R.Clein和H.Rubin提出如下形式的直接效用函數:
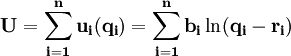 (1)
(1)
(1)式中,
- U表示效用;
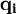 表示第i種商品的實際需求量;
表示第i種商品的實際需求量;
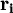 表示可維持生活的第i種商品的基本需求量;
表示可維持生活的第i種商品的基本需求量;
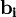 為加權參數,表示消費者對第i種商品的邊際預算份額;
為加權參數,表示消費者對第i種商品的邊際預算份額;
其中,
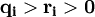 ,
, 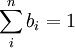 ,且
,且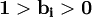 。該效用函數認為,效用具有可加性,且各種商品的效用取決於實際需求量與基本需求量之差。
。該效用函數認為,效用具有可加性,且各種商品的效用取決於實際需求量與基本需求量之差。
另外,消費面臨的預算約束函數為:
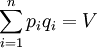 (2)
(2)
(2)式中,
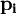 表示第i種商品的價格;
表示第i種商品的價格;
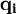 表示第i種商品的實際需求量;
表示第i種商品的實際需求量;
- V表示預算總支出;
該函數表明,一個理性消費者用於購買消費品的支出會在其預算約束之內。
1954年,英國計量經濟學家R.Stone以該直接效用函數為基礎,提出了線性支出系統函數(LES),在預算約束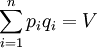 的條件下,極大化直接效用函數,即:
的條件下,極大化直接效用函數,即:
MAX 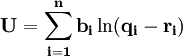
s.t. 
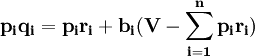 (3)
(3)
(3)式表明,消費者對第i種消費品的消費支出為兩部分之和,第一部分為維持生活的基本消費支出,第二部分為總預算中扣除基本消費支出後對第i種消費品的支出。但是,LES模型存在以下兩個缺陷:一是它沒有考慮到居民把基本消費支出後的餘額用於儲蓄或投資的因素;二是總預算V是對所有商品需求支出之和,為內生變數,無法外生給出,因而模型難以估計。基於以上兩點缺陷,LES模型並沒有在實證中得到廣泛應用。
1973年,經濟學家Luich對LES模型做了兩點修改,提出了擴展線型線型支出系統模型(ELES)。用消費者的收入水平I代替了預算總支出V,用邊際消費傾向βi代替了邊際預算份額bi,模型變為:
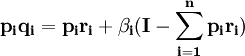 (4)
(4)
該模型表明,在一定收入和價格水平之下,消費者首先滿足其對某種商品或勞務的基本需求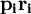 ,在餘下的收入
,在餘下的收入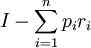 中,按照βi的比例在消費第i種商品和儲蓄之間進行分配,消費者的邊際儲蓄傾向為
中,按照βi的比例在消費第i種商品和儲蓄之間進行分配,消費者的邊際儲蓄傾向為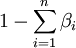 ,且有
,且有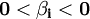 ,
,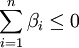 。
。
對(4)式進行處理,寫作:
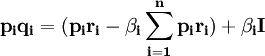 (5)
(5)
採用截面數據時,(5)式中的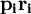 和
和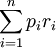 都是不變的常數,從而可以令
都是不變的常數,從而可以令
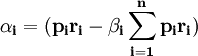 (6)
(6)
令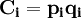 表示居民對第i種商品的實際消費額。則(5)式可以改寫成計量經濟模型:
表示居民對第i種商品的實際消費額。則(5)式可以改寫成計量經濟模型:
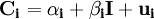 (7)
(7)
其中,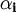 和
和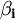 為待估參數,
為待估參數,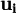 為隨機擾動項。對(7)式採用最小二乘估計,得到參數估計值
為隨機擾動項。對(7)式採用最小二乘估計,得到參數估計值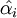 和
和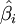 ,然後根據定義:
,然後根據定義: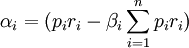 (6),對該式兩邊求和,得到:
(6),對該式兩邊求和,得到:
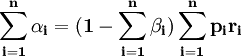 (8)
(8)
將(8)式帶入(6)式,就可得:
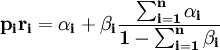 (9)
(9)
再由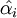 、
、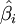 和(9)式,就可以估計出居民對第i種商品的基本需求
和(9)式,就可以估計出居民對第i種商品的基本需求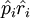 。同時可以求出需求的收入彈性為:
。同時可以求出需求的收入彈性為:
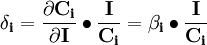
自價格彈性為:
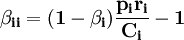
可以發現運用擴展線性支出系統進行消費結構分析,較恩格爾函數模型及其它模型有著明顯的優越性:它可以直接運用截面資料進行參數估計,還可以用來進行邊際消費傾向分析,需求收入彈性分析,基本需求分析。因此擴展線性支出系統是目前較為優越的一種分析方法。








謝謝!