斯塔克爾伯格模型

出自 MBA智库百科(https://wiki.mbalib.com/)

斯塔克爾伯格模型或稱斯塔克爾伯格競爭 (Stackelberg Leadership Model, Stackelberg Competition)由德國經濟學家斯塔克爾伯格（H. Von Stackelberg）在上世紀30年代提出。

　　在古諾模型和伯特蘭德模型里，競爭廠商在市場上的地位是平等的，因而它們的行為是相似的。而且，它們的決策是同時的。當企業甲在作決策時，它並不知道企業乙的決策。但事實上，在有些市場，競爭廠商之間的地位並不是對稱的，市場地位的不對稱引起了決策次序的不對稱，通常，小企業先觀察到大企業的行為，再決定自己的對策。德國經濟學家斯塔克爾伯格建立的模型就反映了這種不對稱的競爭。

　　該模型的假定是：主導企業知道跟隨企業一定會對它的產量作出反應，因而當它在確定產量時，把跟隨企業的反應也考慮進去了。因此這個模型也被稱為“主導企業模型”。

　　假設廠商1先決定它的產量，然後廠商2知道廠商1的產量後再作出它的產量決策。

　　因此，在確定自己產量時，廠商1必須考慮廠商2將如何作出反應。

　　其他假設與古諾模型相同，

　　斯塔克爾伯格模型是一個產量領導模型，廠商之間存在著行動次序的區別。產量的決定依據以下次序：領導性廠商決定一個產量，然後跟隨者廠商可以觀察到這個產量，然後根據領導性廠商的產量來決定他自己的產量。需要註意的是，領導性廠商在決定自己的產量的時候，充分瞭解跟隨廠商會如何行動——這意味著領導性廠商可以知道跟隨廠商的反應函數。因此，領導性廠商自然會預期到自己決定的產量對跟隨廠商的影響。正是在考慮到這種影響的情況下，領導性廠商所決定的產量將是一個以跟隨廠商的反應函數為約束的利潤最大化產量。在斯塔克爾伯格模型中，領導性廠商的決策不再需要自己的反應函數。

　　一、斯塔克爾伯格港口競爭機制模型

　　這裡所說的港口競爭指的是同一港口群內不同港口之間的競爭。一個區域內往往形成一個港口群，群內港口面臨共同的陸向或者海向腹地，因而競爭激烈。港口服務的提供需要具備臨海的地理位置，且港口投資的成本大，這些條件的存在限制了港口產業中港口的數量，使得進入港口的產業進入壁壘較大，因而也就決定了港口產業的市場結構。

　　假設在開始階段，某區域只有一個港口1，其內陸腹地流出或流向該腹地的所有產品均通過港口1，那麼港口1完全壟斷市場。假設不存在進入成本，即新港口以任意規模的投資進入均可獲得收益，於是潛在進入者港口2可以以任意規模進入市場，並獲得利潤。下麵基於斯塔克爾伯格模型，從產量方面說明港口之間的競爭。

　　斯塔克爾伯格模型用來描述一個充當領導者角色的廠商與作為追隨者的廠商之間的相互影響。假設在所有的港口中存在一個在該行業中處於支配地位的港口，該處於支配地位的港口是斯塔克爾伯格領導者。斯塔克爾伯格領導者對產量的選擇將直接導致市場價格的變化，從而影響其他追隨者改變自己的產量。同樣，處於支配地位的港口產量(對其貨物、集裝箱的吞吐量的選擇)發生變化，供給的變化導致市場價格(港口貨物、集裝箱裝卸、航運價格、泊位費用等費用)變化，而市場價格的變化又促使其他港口改變各自的產量，以保持利潤最大化。港口之間博弈的主體是能決定港口產量的政府或者企業。假設條件如下：

　　1．有兩個港口1、2，港口1是產量領導者，產量為y₁，港口2是跟隨者，即根據港口1的選擇而選擇產量y₂。市場價格是總產量的函數，即p = f(y₁ + y₂)；反需求函數可以認為是p = a − b(y₁ + y₂)。

　　2．港口1、2均根據自己的產量確定最大化利潤，且兩個港口的邊際成本為0。

　　3．由於港口1在整個行業處於支配地位，港口2將在港口1產量確定的情況下實現利潤最大化，而港口1也知道港口2根據自己產量確定它的產量，即完全信息。

　　4．港口2根據港口1確定產量，對港口2而言，港口1的產量是常量，港口1在選擇產量時也會考慮到其對港口2的影響。

　　由於其成本假設為0，港口2的利潤函數為：

　　，

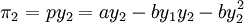　　利潤最大化的條件：，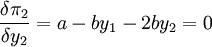

　　所以，求得反應函數：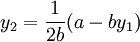

　　將上面的反應函數代入港口1的利潤函數：

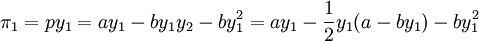
　　其利潤最大化條件：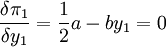

　　所以均衡時港口1最大利潤化的產量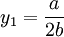

　　那麼，同理可以求出港口2最大利潤化的產量：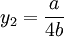

　　在斯塔克爾伯格模型下均衡時兩個港口的產量分別為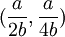：此時港口1、港口2的收益分別為：

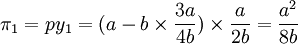
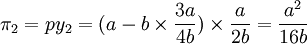
　　這樣，在港口1的產量領導下，港口1和港口2實

　　現了短期的均衡，均衡時的產量為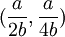，市場價格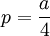。港口1獲得的利潤大於港口2的利潤，說明瞭先動者的優勢，並且，港口1通過產量的選擇限制了港口2的進入規模。

　　二、斯塔克爾伯格港口競爭機制模型的擴展

　　我們定義港口產量是港口投入資本量的函數，存在下列函數關係：Y=f(K)，其反函數K = f ^{− 1}(Y)代表港口產量的多少取決於它的資本存量多少。事實上，進入港口行業需要大量的投資，其沉沒成本很大，需要較大的進入成本。所以，把進入成本F引入模型，在規模收益遞增的情況下，小規模的進入不能獲得利潤。正是因為進入成本大，才使在位者港口可以遏制其他競爭者的進入。

　　在進入成本存在的情況下，港口2進入市場後的利潤函數變為：

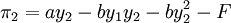
　　那麼，在位者港口1通過制定產量Y₁，使得港口2的最大利潤滿足maxπ₂ = 0，這樣港口2因進入市場無利可圖而不進入，港口1通過產量的選擇阻止港口2進入，阻止進人的產量水平由下式確定：

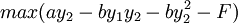
　　港口2取得最大利潤的條件：

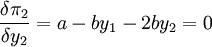
　　所以，當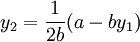 時，港口2的利潤最大，最大利潤為：

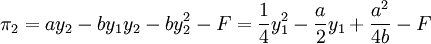
　　港口1選擇自己的產量y₁，使港口2的利潤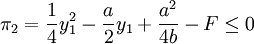

　　若式子 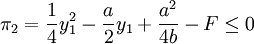，即滿足

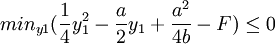
　　y₁=a時，上式有最小值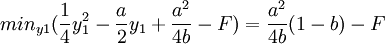

　　所以，當滿足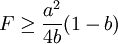時，港口2利潤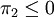

　　下麵分別對幾種情況進行討論：

　　1. 當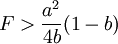 時，

　　y₁的取值範圍滿足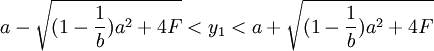時，π₂ < O；

　　y₁取其他值時，π₂ > O。

　　2. 當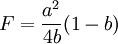 時，y₁ = a時，π₂ = 0；

　　y₁取其他值時，π₂ > 0。

　　3. 當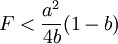 時，π₂ > 0。此時，進入壁壘較小，因而不管港口1怎樣調整自己的產量，都不能阻止港口2進入市場。

　　由上面的模型可以說明港口之間的競爭機制：在位者根據競爭者進入成本的大小選擇遏止其進入還是默許進入策略；而競爭者或者潛在進入者卻只能根據其進入成本大小選擇進入還是不進入市場。港口1要根據港口2進入成本的大小，選擇對港口2的策略。如果港口2的進入成本滿足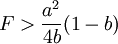，在這種情況下，港口1選擇產量的範圍如果滿足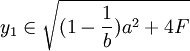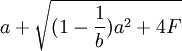，，此時港口1的資本投資存量為K₁ = f ^{− 1}(Y₁)，港口1的資本量構成了進入壁壘，阻止了港口2的進入；如果港口2的進入成本滿足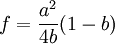，則港口1只需常量調整為y₁ = a，就能使得港口2即使進入市場，其獲得的利潤為π₂ = 0，但是港口1無論選擇除了y₁ = a的任何產量，港口2進入市場均會獲得利潤，此時港口2進入，市場中將會有兩個港口，且港口l是領導者，港口2是跟隨者；如果港口2的進入成本滿足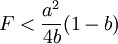，此時的進入成本較小，港口1無論怎樣選擇產量，港口2的進入都會獲得利潤，此時，市場上將存在港口1、港口2兩個港口，港口1是產量領導者，港口2是跟隨者，兩個港口之間的競爭機制是斯塔克爾博格式的競爭。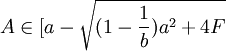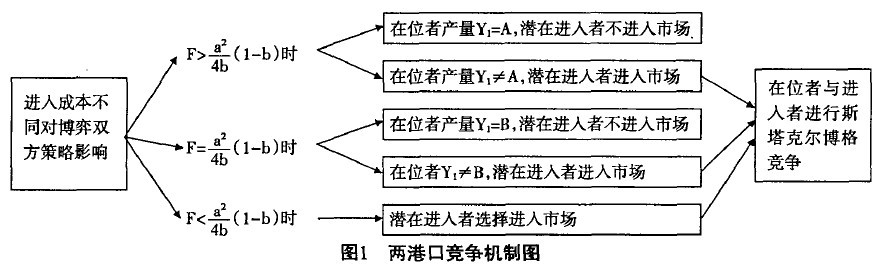記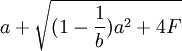，，B=a，兩港口之間的競爭機製圖如圖l所示。

　　三、環渤海港口競爭的實證分析

　　環渤海港口群包括了遼寧、河北、天津和山東的主要港口，包括大小港口60多個，其中包括大連、秦皇島、天津、青島四個億噸大港。環渤海港口群根據地理空問位置可以分為三大子港口群：一是以大連為核心的遼寧港口群，包括錦州港、營口港、丹東港幾個主要支線港；二是以天津為核心的津冀港口群，包括秦皇島港、京唐港、黃驊港等主要支線港；三是以青島港為核心的山東港口群，包括煙臺港、威海港、龍口港、日照港等支線港。 本文所研究的港口競爭，指的是環渤海港口群港口之間內部的競爭，不考慮環渤海港口群中港口與國外港口的競爭，也不考慮環渤海港口群與國內其他港口群之間的競爭。環渤海港口群港口之間的競爭又包括了集群內部樞紐港的競爭和大港與周圍小港之間的競爭。

　　(一)環渤海港口群內部樞紐港的競爭

　　樞紐港是港口的核心，對區域經濟發展起到十分重要的作用。環渤海港口群內部樞紐港的競爭主要集中在大連、天津、青島之間，其中大連港要成為東北亞國際航運中心，天津港要成為北方國際航運中心，而青島港也要成為國際航運中心。

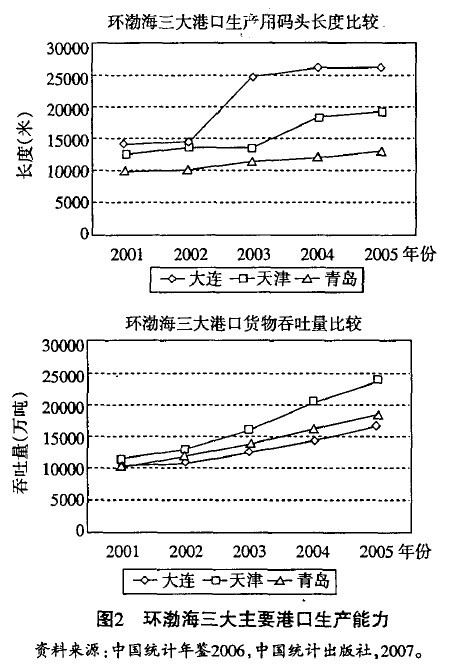
　　港口投資用於增加港口生產用碼頭的長度，進而增加了港口的貨物吞吐能力，或者集裝箱吞吐能力。這三個主要港口的競爭在於對港口規模的投資上，港口之間的競爭以增加對貨物的吞吐量為主，港口通過增加港口碼頭長度和碼頭泊位個數來增加自身的吞吐能力，從圖2中我們可以看出，2002至2003年間，大連港生產用碼頭增長幅度較大，而天津港2003到2004年年間增長幅度較大，青島港生產用碼頭長度雖然增幅不大，但近幾年來一直穩步增加。雖然大連港生產用碼頭的長度大於青島和天津港，但是其貨物吞吐量是其中最小的，可見通過擴大港口規模來增大貨物吞吐量的效果並不明顯，說明港口規模只是影響貨物吞吐量的一個因素。

　　(二)區域內小港之間的競爭

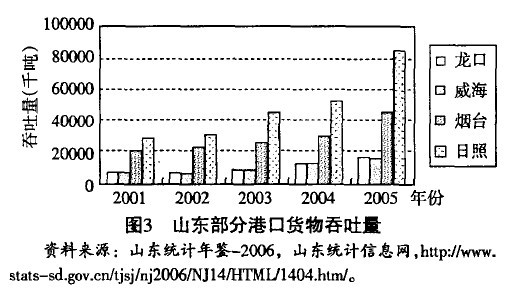
　　區域內大港與周圍小港之間的競爭主要表現為遼寧港口群內港口之間的競爭，津冀港口群內以及山東港口群內港口之間的競爭，產生競爭的原因由於各個港口地理位置上比較接近，所服務的內陸腹地相同或者交叉，而對於貨主而言，選擇他們當中哪個港口其綜合成本沒有區別或者區別不大，因而各港口之間圍繞腹地資源展開競爭。港口腹地的界限並不明確。內陸地區產品出口或進口不一定就近選擇距離港口，他們在選擇港口時考慮的是綜合的成本，不單單是考慮運費，還應考慮影響綜合成本的其他因素，包括港口的效率、航運班次等等。規模較大的港口之間的競爭依靠產量(吞吐量)，通過港口規模的不斷擴大，獲得規模經濟優勢，從而降低自身的平均成本。而小港口由於自然條件的限制，以及巨大的投資成本，不可能象大港口那樣進行巨大的投資以獲得規模經濟，因而規模小的港口主要通過降低服務價格，提高服務質量來爭奪腹地資源，在貨主通往其他港口的運輸成本一致的情況下，通過降低其他方面的成本達到降低貨主的綜合成本，以此來吸引貨源。

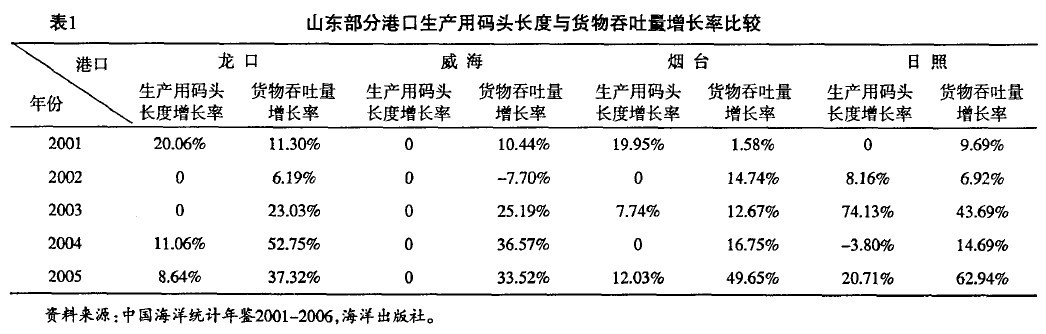
　　由圖3可以看出，山東港口群的這些港口年貨物吞吐能力整體上逐年上升，在沒有考慮青島的情況下，貨物吞吐量最大的是日照，到2005年，日照港的貨物吞吐量達到84 208千噸，煙臺港2005年的貨物吞吐量達到45 060千噸，龍口港和威海港這兩個港口的年貨物吞吐量類似，幾年來也處於緩慢上升階段。但是，這些港口的貨物吞吐量增長比率並不與其生產用碼頭長度增長率相一致。在不考慮其他因素的條件下，生產用碼頭長度的增加到第二年才會表現出貨物吞吐能力的增長。表1所列的是各年來山東部分港口生產用碼頭長度增長率與貨物吞吐量增長率，從表中我們可以看出，前一年生產用碼頭長度並不一定與後一年吞吐量有著正相關的關係，或者說，即使生產用碼頭長度的增加並不一定能使吞吐量在下一年有所增長。這就說明瞭港口規模的擴大不一定是港口貨物吞吐量增加的主要原因，還有其他因素影響這港口的貨物吞吐量，小港口之間的競爭，通過投資增加吞吐量，這種競爭方式不是很明顯，而是通過其它方式來爭奪貨源。

　　根據以上的分析，我們可以看出，無論是生產用碼頭的增加還是貨物吞吐量的增加，都是擴大港口規模的結果，這也說明瞭環渤海港口之間的競爭機制，即圍繞產量進行競爭，各個港口均通過規模的擴大獲得更多的市場份額，也充分說明原來原先潛在進入者進入市場的進入壁壘並不足以限制其進入，因而在位者也無法通過自身產量的選擇來限制其他潛在進入者的進入，對跟隨者港口的策略影響也較小，競爭的結果是潛在進入者最終進入市場，作為領導者的港口和作為跟隨者的港口均擴大產量，增加對貨物的吞吐能力，各個港口通過貨物吞吐能力的增加展開競爭。

　　之所以作為產量領導者的大港和作為跟隨者的小港展開產量競爭，以及作為潛在進入者的其他競爭者進入市場，充分說明港口產業的市場結構還處於寡頭或者壟斷競爭中，港口數量還沒有足夠的多，只要潛在進入者進入該市場的預期收益高於其進入成本，潛在進入者就會進入，直至市場的飽和或者說是達到近似完全競爭狀態。當然，建立一個港口需要有適合的自然條件，這也就在一定程度上限制了港口產業中的港口數目，進而決定了各個港口之間的競爭是不完全競爭，從而使得以擴大產量為主的競爭機制得以運行。

　　四、對策措施

　　港口之間的適度競爭，有助於提高港口的服務效率，降低物流成本，可以增強港口的國際競爭力，促進港口的發展。但是，我們在提倡港口競爭的同時，要避免或者減少港口的盲目競爭、惡性競爭。由於整個環渤海港口群由於在地域上的相似性，再加上港口功能的可替代性，導致了群內各個港口相互爭奪腹地資源，在這個過程中，各個港口運用各種手段，容易造成港口的盲目競爭，盲目競爭主要指港口間的同質化、低水平化的競爭，表現在數量、價格方面的競爭。港口之間的盲目競爭將造成很大的問題：首先，巨大的資本投入造成了資源的浪費。盲目競爭會造成對港口的大規模投入，港口投資費用高，而且時間長，如果過多的資本投資於港口建設中，形成大量的重覆建設，將會造成資本的大量浪費，不利於國民經濟的增長；其次，港口的盲目競爭容易造成整個環渤海港口群整體上開發的盲目性，使環渤海港口群內港口格局混亂，不利於形成對外的核心競爭力；第三，港口的盲目競爭，不利於港口的專業化、技術化水平的提高。盲目競爭使得各個港口往往只註重增加吞吐量，而忽視了增加吞吐量的方式，各個港口容易只將重點放在規模的擴大上，忽視港口作業的專業化、技術化水平的提高；最後，盲目競爭使得在對海岸線資源進行開發的過程中只註重開發，而對海岸線資源的保護程度不夠。由於海岸線資源是不可再生資源，無秩序的開發不利於可持續發展。

　　鑒於上述問題，我們在保證港口競爭的同時，還要遏制盲目競爭、惡性競爭，因而提出以下建議。

　　1．環渤海港口群要根據自身優勢，加強港口之間的分工和協作，通過分工與協作，作好港口資源的整合工作。港口之間的分工與合作主要是大港與大港、小港與小港以及大港與小港之間的分工與合作。大港之間，小港之間要根據自身優勢來進行分工，而大港與小港之間，主要是小港作好支線服務，為區域大港、樞紐港吸引更多的貨源。港口之間更好的進行分工和協作，有助於實現區域內港口資源的合理配置，避免了港口的重覆建設。要實現港口的分工合作，需要發揮港口優勢，實現環渤海港口群的一體化。由於環渤海港口群的各個港口分屬於不同的省市，因而港口之間能否進行分工和協作關鍵要看省市之間的協商，以及利益分配。

　　2．提倡港口的“錯位競爭”、合理競爭。各個港口應對港口功能進行合理定位，根據自身情況選擇港口的主要功能，比如樞紐型港口、腹地型港口或者轉口型港口的轉變，以及選擇作為基本港還是非基本港。港口競爭是不可避免的，關鍵是要避免惡性競爭，港口之間要進行合理的競爭。合理的競爭就是港口之間服務質量、效率水平上的競爭，以此代替以前的港口間的數量、價格競爭，促進整個港口群的結構優化。

　　3．政府相關部門應制定合理的港口發展規劃，同時政府部門要對港口建設發揮監督管理作用。由於港口對於國家和地區的經濟發展有著極為重要的作用，因而港口的發展應該有個合理的長遠的計劃，在考慮到港口所在區域發展的同時，還要兼顧國家利益。由於環渤海港口群內的港口分屬於不同的行政區，各個省市在制定各自的港口發展戰略時要充分考慮到整個港口群的發展，各省市要加強溝通和聯繫，在保證國家利益的前提下制定轄區內的港口發展戰略。

　　4．擴展港口物流戰略聯盟。戰略聯盟指企業之間利用股權或契約方式形成的一種組織形式，而港口聯盟是戰略聯盟的一種具體的表達方式，是港口與港口間為了得到更大的收益通過協商達成一致對外形式。它既可指幾個港口組成的集團，也可指與船公司的聯盟，與內陸運輸組織的聯盟等。為了使環渤海港口群內港口資源得到有效利用，需拓展國內外港口戰略聯盟，尤其在物流方面。通過戰略聯盟的擴展可以擴大港口服務的範圍，有利於增加港口產量而又避免了港口之間在產量上的惡性競爭。

• 伯特蘭德模型
• 斯威齊模型
• 古諾模型
• 埃奇沃斯模型