貼現因數
出自 MBA智库百科(https://wiki.mbalib.com/)
貼現因數(discount factor),也稱折現繫數、折現參數、折現因數
目錄 |
所謂貼現因數,就是將來的現金流量折算成現值的介於0-1之間的一個數。
一般來說,當利率為r時,承諾T年之後支付R美元的現值是R美元/(1+r)^T。因此,即使沒有通貨膨脹,將來1美元的價值也小於現在1美元的價值,必須按某一數額貼現,該數額取決於利率的高低和收到貨幣的時間長短。其中1/ (1+r)^T被稱為未來T時期的貨幣的貼現因數(discount factor)。 (註:^T表示T次方) 貼現因數δ=1/(1+r)^T,0<δ<1,r是貼現率。貼現值為1/(1-δ)^T
在計算現值時,貼現因數起著很重要的作用:

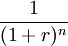
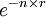
貼現因數在數值上可以理解為貼現率,就是1個份額經過一段時間後所等同的現在份額。這個貼現因數不同於金融學或者財務學的貼現率之處在於,它是由參與人的“耐心”程度所決定的。“耐心”實質上是講參與人的心理和經濟承受能力,不同的參與人在談判中的心理承受能力可能各不相同,心理承受能力強的可能最終會獲得更多的便宜;同樣,如果有比其他參與人更強的經濟承受能力,也會占得更多的便宜。
學者在博弈論對貼現因數的定義:
貼現因數是討價還價博弈中的一個很重要的概念,Gibbons將貼現因數定義為“貨幣的時間價值”,實際上就是貼現率=1/1+r;
張維迎的博弈論中將貼現因數解釋為參與人的耐心程度,貼現因數表示一個參與人的耐心程度,取值在『0,1』,越大說明參與人的耐心越好,若是等於0則說明參與人完全沒有耐心。由於貼現因數是由公式 1/1+r定義的,那麼可以看到,收益率越大,則貼現因數越小,則參與人的耐心程度越小;反之,如果收益率越小,則貼現因數越大,參與人越有耐心。
關於貼現因數的討論[1]
行為經濟學的研究目前越來越受到人們的重視,特別是今年諾貝爾經濟學獎授予了研究實驗經濟學和行為經濟學的經濟學家以後。行為經濟學的研究就是在考慮人們的決策過程中要註重人們的行為對決策的影響,如在分析資產定價理論時,Caplin 和Leahy(2001)考慮了人們對風險的緊張程度來考慮資產定價行為, Barberis, Huang和Santos(2001)考慮人們的預期行為對資產定價的影響,Abel (1990), Constantinides (1990), Sunderason (1989)和Campbell和Cochrane (1999)引入“習慣資本”形成對資產定價的影響;在考慮經濟增長時,Kurz(1968),Zou(1994,1996)引入人們對社會地位的追求來討論這種追求對經濟增長的影響;Carroll 和Samwick(1997)和Carroll,Overland 和Weil (2000) 討論“習慣資本”對經濟增長的影響等等,諸如此類的模型都考慮了人們行為對經濟決策的影響。實際上,在經濟學中,人們已經早就註意到了個體行為對經濟的影響,如我們通常所講的效用函數就是基於人們對商品的偏好形成的,同時在研究人們的決策過程中,考慮人們的跨時決策行為時不可避免地要涉及到人們對將來的耐心程度,這就是經濟學中經常提到的貼現因數。
關於貼現因數的討論必須要追溯到人們對跨時選擇問題的研究。關於人們對跨時選擇的討論可以追溯到Adam Smith的著作“《國富論》”,但是,是蘇格蘭經濟學家John Rae 最早考慮了人們在跨時選擇過程中的社會行為和心理行為,提出了跨時選擇的必要條件,但是,所有的這些討論,直到1937年Samuelson 給出了貼現效用模型才使得經濟學家對跨時選擇的研究有了理論基礎,雖然Samuelson 給出的貼現效用模型很簡單,也具有較大的局限性,但是這個模型一經給出就立即被人們接受,而且被廣泛地引用,這主要是因為它不僅是公共跨時選擇的理論基礎,也是對人們實際行為的較好描述。貼現效用模型的重要假設就是人們在不同時間獲得的效用可以用一個簡單因數來區分,這個因數就是貼現因數,它表示了人們對將來的耐心程度。為簡單起見,Samuelson把它看成是一個常數,也就是說人們在今天對明天,和人們處於明天對後天的耐心程度是一致的。這個假設當然具有很大的局限性,在Samuelson以後的經濟學家對貼現因數作了很多重大的改進。主要有:Uzawa (1968) 給出的內生貼現因數模型,Becker和Mulligan(1997)提出貼現因數模型,Laibson(1997,2001)給出了雙曲貼現因數模型,Marshall的貼現因數模型,Takashi Kamihigashi(2002)給出的非線性貼現因數模型和Gong和Zou的貼現因數模型(2002)。
- ↑ 龔六堂.貼現因數、偏好和行為經濟學







