邊際分析方法
出自 MBA智库百科(https://wiki.mbalib.com/)
邊際分析方法(marginal analysis/marginal adding analysis)
目錄 |
邊際分析法是這一時期產生的一種經濟分析方法,同時形成了經濟學的邊際效用學派,代表人物有瓦爾拉(L. Walras)、傑文斯(W.S. Jevons)、戈森(H.H. Gossen)、門格爾(C. Menger)、埃奇沃思(F.Y. Edgeworth)、馬歇爾(A. Marshall)、費希爾(I. Fisher)、克拉克(J.B. Clark)以及龐巴維克(E. von Bohm-Bawerk)等人。邊際效用學派對邊際概念作出瞭解釋和定義,當時瓦爾拉斯把邊際效用叫做稀缺性, 傑文斯把它叫做最後效用,但不管叫法如何,說的都是微積分中的“導數”和“偏導數”。
在西方經濟學中,邊際分析方法是最基本的分析方法之一,是一個比較科學的分析方法。西方邊際分析方法的起源可追溯到馬爾薩斯。他在1814年曾指出微分法對經濟分析所可能具有的用途。1824年,湯普遜(W.Thompson)首次將微分法運用於經濟分析,研究政府的商品和勞務採購獲得最大利益的條件。功利主義創始人邊沁(J.Bentham)在其最大快樂和最小痛苦為人生追求目標的信條中,首次採用最大和最小術語,並且提出了邊際效應遞減的原理。
邊際分析法是把追加的支出和追加的收入相比較,二者相等時為臨界點,也就是投入的資金所得到的利益與輸出損失相等時的點。如果組織的目標是取得最大利潤,那麼當追加的收入和追加的支出相等時,這一目標就能達到。
邊際分析法的數學原理很簡單。對於離散discrete情形,邊際值marginal value為因變數變化量與自變數變化量的比值;對於連續continuous情形,邊際值marginal value為因變數關於某自變數的導數值。所以邊際的含義本身就是因變數關於自變數的變化率,或者說是自變數變化一個單位時因變數的改變數。在經濟管理研究中,經常考慮的邊際量有邊際收入MR、邊際成本MC、邊際產量MP、邊際利潤MB等。
邊際分析方法在西方經濟學中,我們把研究一種可變因素的數量變動會對其他可變因素的變動產生多大影響的方法,稱為邊際分析方法。
邊際分析法就是運用導數和微分方法研究經濟運行中微增量的變化,用以分析各經濟變數之間的相互關係及變化過程的一種方法。
邊際即“額外的”、“追加”的意思,指處在邊緣上的“已經追加上的最後一個單位”,或“可能追加的下一個單位”,屬於導數和微分的概念,就是指在函數關係中,自變數發生微量變動時,在邊際上因變數的變化,邊際值表現為兩個微增量的比。
這種分析方法廣泛運用於經濟行為和經濟變數的分析過程,如對效用、成本、產量、收益、利潤、消費、儲蓄、投資、要素效率等等的分析多有邊際概念。
邊際分析法之所以成為西方經濟學研究中的非常重要的方法,是由西方經濟學的對象決定的。由於西方經濟學研究資源最優效率的使用,而最優點實際就是函數的極值點,根據高等數學的知識,很容易理解,數學方法求得極值就是對函數求導數,當它的一階導數為0時,即找到極值點。
經濟學研究經濟規律也就是研究經濟變數相互之間的關係。經濟變數是可以取不同數值的量,如通貨膨脹率、失業率、產量、收益等等。經濟變數分為自變數與因變數。自變數是最初變動的量,因變數是由於自變數變動而引起變動的量。例如,如果研究投入的生產要素和產量之間的關係,可以把生產要素作為自變數,把產量作為因變數。自變數(生產要素)變動量與因變數(產量)變動量之間的關係反映了生產中的某些規律。分析自變數與因變數之間的關係就是邊際分析法。
“邊際”這個詞可以理解為“增加的”的意思,“邊際量”也就是“增量”的意思。說的確切一些,自變數增加一單位,因變數所增加的量就是邊際量。比如說,生產要素(自變數)增加一單位,產量(因變數)增加了2個單位,這因變數增加的兩個單位就是邊際產量。或者更具體一些,運輸公司增加了一些汽車,每天可以多運200多名乘客,這200名乘客是邊際量。邊際分析法就是分析自變數變動一單位,因變數會變動多少。
經濟學家提出“邊際”和“邊際分析”的概念不是故弄玄虛,而是為了作出更正確的決策。經濟學家常說,理性人要用邊際量進行分析就是這個道理。
我們可以用最後一名乘客的票價這個例子來說明邊際分析法的用處。當我們考慮是否讓這名乘客以30元的票價上車時,實際上我們應該考慮的是邊際成本和邊際收益這兩個概念。邊際成本是增加一名乘客(自變數)所增加的成本(因變數)。在我們這個例子中,增加這一名乘客,所需磨損的汽車、汽油費、工作人員工資和過路費等都無需增加,對汽車來說多拉一個人少拉一個人都一樣,所增加的成本僅僅是發給這個乘客的食物和飲料,假設這些東西值10元,邊際成本也就是10元。邊際收益是增加一名乘客(自變數)所增加的收入(因變數)。在這個例子中,增加這一名乘客增加收入30元,邊際收益就是30元。
在根據邊際分析法作出決策時就是要對比邊際成本與邊際收益。如果邊際收益大於邊際成本,即增加這一名乘客所增加的收入大於所增加的成本,讓這名乘客上車就是合適的,這是理性決策。如果邊際收益小於邊際成本,讓這名乘客上車就要虧損,是非理性決策。從理論上說,乘客可以增加到邊際收益與邊際成本相等時為止。在我們的例子中,私人公司讓這名乘客上車是理性的,無論那個售票員是否懂得邊際的概念與邊際分析法,他實際上是按邊際收益大於邊際成本這一原則作出決策的。國營公司的售票員不讓這名乘客上車,或者是受嚴格制度的制約(例如,售票員無權降價),或者是缺“邊際”這根弦。我們常說國營企業經營機制不如私人企業靈活,這大概可以算一個例子。
邊際分析法在經濟學中運用極廣。所以,邊際這個概念和邊際分析法的提出被認為是經濟學方法的一次革命。在經濟學中,邊際分析法的提出不僅為我們作出決策提供了一個有用的工具,而且還使經濟學能運用數學工具。邊際分析所表示的自變數與因變數之間變動的關係可以用微分來表示。由此數學方法在經濟學中可以得到廣泛應用。現在數學在經濟學中運用十分廣泛,對推動經濟學本身的發展和解決實際經濟問題起到了重大作用。有興趣的讀者看一點更高深的經濟學著作就會體會到這一點。
在經濟學上,邊際是指每單位投入所引起的產出的變化。邊際分析方法在管理經濟學中有較多的應用。它主要分析企業在一定產量水平時,每增加一個單位的產品對總利潤產生的影響。可以用以下的公式來說明。
公式:邊際值=△f(x)/△X
其中,X代表投入,f(x)代表產出,表現為X的函數;△表示變數。
假設基數X處在變化中,那麼,每增加一個單位的投入,這個單位所引起的產出的增量是變化的。
比較分析法在西方經濟學中受到特別重視,1870年代由法國的瓦爾拉斯、奧地利的門格爾、英國的傑文斯幾乎同時提出來,後被稱為“邊際革命”。這種方法有以下幾個特點:
其一,邊際分析是一種數量分析,尤其是變數分析,運用這一方法是研究數量的變動及其相互關係。這一方法的引入,使經濟學從常量分析發展到變數分析,這一點從概念上已經說明瞭。事實上,在經濟活動中,恰恰是自變數的微量變動所引起的因變數的變化程度極少相等,即不是直線型,大量是變化率不等的曲線型。邊際分析法研究微增量的變化及變數之間的關係,可使經濟理論精細地分析各種經濟變數之間的關係及其變化過程,就是說,它對經濟變數相互關係的定量分析更嚴密。
其二,邊際分析是最優分析。邊際分析實質上是研究函數在邊際點上的極值,要研究因變數在某一點遞增、遞減變動的規律,這種邊際點的函數值就是極大值或極小值,邊際點的自變數是作出判斷並加以取捨的最佳點,據此可以作出最優決策,因此是研究最優化規律的方法。
其三,邊際分析是現狀分析。邊際值是直接根據兩個微增量的比求解的,是計算新增自變數所導致的因變數的變動量,這表明,邊際分析是對新出現的情況進行分析,即屬於現狀分析。這顯然不同於總量分析和平均分析,總量分析和平均分析實際上是過去分析,是過去所有的量或過去所有的量的比。在現實社會中,由於各種因素經常變化,用過去的量或過去的平均值概括現狀和推斷今後的情況是不可靠的,而用邊際分析則更有利於考察現狀中新出現的某一情況所產生的的作用、所帶來的後果。
邊際分析法在1870年代提出後,首先用於對效用的分析,由此建立了理論基礎——邊際效用價值論。這一分析方法的運用可以說引起了西方經濟學的革命,具體說它的意義表現為:
第一,邊際分析的運用使西方經濟學研究重心發生了轉變。由原來帶有一定“社會性、歷史性”意義的政治經濟學轉為純粹研究如何抉擇把有限的稀缺資源分配給無限而又有競爭性的用途上,以有效利用。
第二,邊際分析開創了經濟學“數量化”的時代。邊際分析本身是一種數量分析,在這個基礎上,使各種數量工具線性代數、集合論、概率論、拓撲學、差分方程等,逐步滲入經濟學,數量化分析已經成為西方經濟學的主要特征。
第三,邊際分析導致了微觀經濟學的形成。邊際分析以個體經濟活動為出發點,以需求、供給為重心,強調主觀心理評價,導致了以“個量分析”為特征,以市場和價格機制為研究中心的微觀經濟學的誕生。微觀經濟學正是研究市場和價格機制如何解決三大基本經濟問題,探索消費者如何得到最大滿足,生產者如何得到最大利潤,生產資源如何得到最優分配的規律。
第四,邊際分析奠定了最優化理論的基礎。在邊際分析的基礎上,西方經濟學從理論上推出了所謂最優資源配置,最優收入分配,最大經濟效率及整個社會達到最優的一系列條件和標準。
第五,邊際分析使實證經濟學得到重大發展。研究變數變動時,整個經濟發生了什麼變動,這為研究事物本來面目、回答經濟現象“是什麼”問題的實證經濟學提供了方法論基礎。
◆ 邊際收益:每增加一個單位的產品所帶來的收益增量
企業在判斷一項經濟活動對企業的利弊時,不是依據它的全部成本,而是依據它所引起的邊際收益與邊際成本的比較。若前者大於後者,這項活動就對企業有利,反之則不利。
邊際分析法體現向前看的決策思想,是尋求最優解的核心工具。主要應用如下:
1、無約束條件下最優投入量(業務量)unconstrained optimization的確定:
利潤最大化是企業決策考慮的根本目標。由微積分基本原理知道:利潤最大化的點在邊際利潤等於0的點獲得。利潤(或稱凈收益)為收入與成本之差,邊際利潤亦即邊際收入與邊際成本之差,即:MB=MR-MC。
由此可以獲得結論:只要邊際收入大於邊際成本,這種經濟活動就是可取的;在無約束條件下,邊際利潤值為0(即:邊際收入=邊際成本)時,資源的投入量最優(利潤最大)。
2、有約束條件下最優業務量constrained optimization分配的確定:
對於有約束情形可以獲得如下最優化法則:在有約束條件下,各方向上每增加單位資源所帶來的邊際效益都相等,且同時滿足約束條件,資源分配的總效益最優。這一法則也稱為等邊際法則。
當所考慮的資源是資金時,有約束的最優化法則即為:在滿足約束條件的同時,各方向上每增加一元錢所帶來的邊際效益都相等;如果資金是用來購買資源,而各方向的資源價格分別都是常數,有約束的最優化法則即為:在滿足約束條件的同時,各方向上的邊際效益與價格的比值都等於一個常數。
3、最優化原則的離散結果:當邊際收益大於邊際成本時,應該增加行動;當邊際收益小於邊際成本時,應該減少行動;最優化水平在當邊際成本大於邊際收益的前一單位水平達到。
4、提倡使用增量分析。增量分析是邊際分析的變形。增量分析是分析某種決策對收入、成本或利潤的影響。這裡"某種決策"可以是變數的大量變化,包括離散的、跳躍性的變化,也可以是非數量的變化,如不同技術條件、不同環境下的比較。比較不同決策引起的變數變化值進行分析。
在管理決策中應用邊際分析法相當於是建立了一套有利於決策的評價體系:不僅考慮變數的總值Total,也同時考慮變數的平均值Average和邊際值 Marginal。總值、平均值與邊際值之間具有如下關係(total-average-marginal relationship):
1)邊際值的符號是總值上升或下降的信號;
2)當邊際值大於平均值時,平均值處於遞增狀態。
有可能的話對上述結論進行數學推導,細化結論的文字描述,這可以加深對結論的理解應用。特別註意4個重要點位:盈虧平衡點、邊際利潤最大點、平均利潤最大點、總利潤最大點。
應用邊際分析法還隱含著一個思想:充分利用與促進開發信息資源。
在應用邊際方法或最優化方法也應該註意如下複雜因素:
1、現實經濟管理問題總是千絲萬縷,存在多個變數,要爭取抓住主要變數,併在各個方向上滿足邊際法則;
2、決策變數與相關結果之間關係複雜,所選取的變數是否得當,必須定量分析與定性分析相結合,併進行方程回歸、曲線擬合、顯著性檢驗等檢驗處理;
3、註意所考慮問題存在各種各樣的約束條件和數學工具的應用條件;
4、註意決策問題存在的不確定性和風險。
◆ 確定規模。規模的大小直接影響到企業的生產效益。當一個企業要擴大規模時,它就要分析每增大一個單位的規模,所可能帶來的產出的增量,這就是邊際分析。科學的邊際分析方法可以使企業的規模確定在一個最合理的範圍內。
公式:π=MR-MC
其中,π代表邊際利潤,MR代表邊際收益,MC代表邊際成本。
當π>0時,增加一個單位的產品,獲得的收益增量比引起的成本增量大,說明企業還沒有達到能夠獲得最大收益的產量規模,此時,企業應該擴大產量。
當π<0時,增加一個單位的產品,所引起的成本增量比所能獲得的收益增量要大,說明企業應該減小產量。
當π=0時,企業達到最優的產量規模。
◆ 價格決策。每提高(或降低)一個單位的價格,對總收益會產生什麼樣的影響,這實際上也要用到邊際分析方法,它可以幫助企業制定具有競爭力的價格戰略。
◆ 確定合理的要素投入。在確定生產中需要投入的各個要素的量時,我們需要分析每增加一個單位的某種要素時,對總的收益會產生什麼影響。這也是邊際分析。
◆ 產品結構分析。多數企業都不只生產一個產品,各個產品生產的比例就是產品結構。確定各個產品生產多少的比例關係就可以運用邊際分析方法--對各個產品的邊際效益進行分析。所謂邊際效益,就是對一個產品的生產增加一個單位的資金投入所引起的收益的變化量。如果把資金增量投入到各個產品,所能產生的邊際效益是相等的,那麼這個企業的產品結構就是合理的;否則,其中必定有某種產品值得擴大規模,以帶來更多的收益。針對產品結構進行邊際分析,可以明確哪些產品需要增加投入,哪些產品需要縮小生產規模。
案例一:邊際效用分析方法在經濟微觀理論中的運用[1]
邊際效用分析方法作為觀察消費者行為的一個工具,只有一定的實用性。按照西方經濟學的理論,效用是商品(包括勞務)滿足人們欲望的能力。它決定消費者的偏好,從而決定對商品的需求。對消費者來說,有的商品的邊際效用高,有的商品的邊際效用低,為取將最大效J隊他必鬚根據邊際效用隨購買量增加而遞減的規律,多購買邊際效用高的商品,少購買邊際效用低的商品,達到消汝科均衡,即消費者所花費的每一元錢都取得相等的邊際效用(簡稱邊際效用均等或單位貨幣邊際效用相等)。
西方經濟學家迎過對消費者行為的分析,發現了邊際效用遞減規律和邊際效用均等規律,但卻無法將邊際效用分析方法運用於巨集觀領域。其實巨集觀邊際效用不過是微觀邊際效用的總和。例如,在一定時期(一年或一個月)如果所有消費者都認為自己所購買的商品的邊際效用是均等的,則巨集觀邊際效用也必然是均等的。而作為所有消費者購買量總和的各種商品社會銷售量,則是僅各種商品的巨集觀邊際效用達到均等的推動力。巨集觀邊際效用趨於均等的過程可簡單描述如下:在一定時期,各個消費者選購商品,如果他們感到自己所購買的商品的邊際效用不均等,會不斷調整購買量,直到實現消費者均衡,巨集觀邊際效用也隨之達到均等。
巨集觀邊際效用與微觀邊際效用相同之處是,都能根據購買量的大小來判斷邊際效用的高低,都具有趨於邊際效用均等的傾向。不同之處是,巨集觀邊際效用還存在著邊際效用遞增規律,即在其它條件不變的情況下,商品的巨集觀邊際效用隨著消費者對其需求的增加而遞增。因為消費者對商品需求的增加,會拉大供求差距,使其變得相對稀缺,從而增大消費者對該商品的欲望強度,導致其巨集觀邊際效用上升。由此可見,巨集觀邊際效用主要取決於供給和需求兩個因素。其公式為:
|
巨集觀邊際效用= | 需求 | |
| 供求 |
該公式表明需求越大於供給,巨集觀邊際效用越大;需求越小於供給,巨集觀邊際效用越小。由於各種商品的單位貨幣的巨集觀邊際效用從不相等到相等,是通過增減銷售量(供給量)來實現的,即增加巨集觀邊際效用高的商品的購買量(銷售量),使之降下來,減少巨集觀邊際效用低的商品的購買量,使之升上來,最終達到各種商品的巨集觀邊際效用均等。因此銷售量增長率高的商品,其巨集觀邊際效用也高,銷售量增長率低的商品,其巨集觀邊際效用也低。
邊際效用遞增規律揭示出需求增加直接導致巨集觀邊際效用上升的因果關係,表明在一定條件下巨集觀邊際效用的高低,取決於社會需求量的大小或需求收入彈性的強弱。從巨集觀邊際效用的變化過程看,某商品在剛試製出來時,由於受到收入的限制,只有少數人買得起,因而需求量比較小。以後,隨著人們收入的提高,有支付能力的社會需求也相應增加。但在這一時期,願意井有能力購買的人雖然不斷增加,但增加量比較小,因而需求收入彈性較低,相應的,巨集觀邊際效用也較低,這是商品的巨集觀邊際效用發展的第一階段,即巨集觀邊際效用較低的階段。
當人們的收入提高到一定程度,購買者的增加速度由慢轉快,出現購買商潮,並一直延續到需求接近相對飽和。在這一時期,該商品的需求收入彈性較高,收入的每一次提高都會帶來需求的較大增加,因而巨集觀邊際效用相對較高,這是該商品的巨集觀邊際效用發展問第二階段,即高巨集觀邊際效用階段。在人們對該商品的需求得到一定程度滿足後,儘管收入繼續提高,但其需求增加很少,甚至會下降,因而巨集觀邊際效用相對較低,這是該商品的巨集觀邊際效用發展的第三階段,即巨集觀邊際效用較低的階段。
可以說,任何消費品的巨集觀邊際效用隨著人們收入的提高,部型經歷一個從低到高,再從高到低的發展過程。或者說,都要經歷上述三個發展階段。這是巨集觀邊際效用的基本規律。
但各種商品的巨集觀邊際效用不可能同時處於同一發展階段,在一定時期,有的商品的巨集觀邊際效用處於第一階段,該類商品稱為第一類商品;有的商品的巨集觀邊際效用處於第二階段,該類商品稱為期二類商品;有的商品的巨集觀邊際效用處於第三階段。該類商品稱為第三類商品。這樣,全部消費品可以分為上述三類商品。但它們個足一成不變的,根據巨集觀邊際效用基本規律,隨著供給的增加,處於第一階段的巨集觀邊際效用要轉入第二階段,處於第二階段的巨集觀邊際效月1要轉入第三階段。與之相應,第一類商品要轉變為第二類商品,第二類商品要轉變為第三類商品。於是,全部消費品的演變歷史可以表述為這樣一個過程:第一類商品不斷轉變為第二類商庸4I第二類商船不斷轉變為第三類商品,第三類商品逐漸走向衰亡,同時新發明創造出來的商品又不斷補充第一類商品。這是消費品發展的基本規律。
案例二:邊際分析法在企業改革中的運用[2]
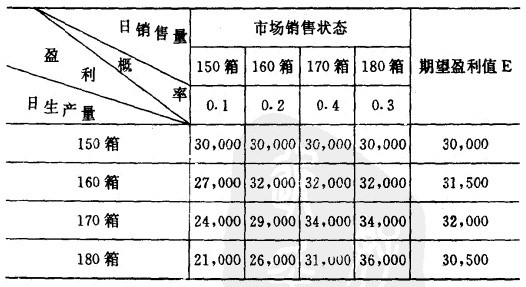
某企業生產、銷售一種產品,成本500元/箱,售價700元/箱,如當天滯銷,按每箱200元進行處理,根據該企業的上述情況確定其最佳日銷售量。根據該企業的歷史資料進行統計分析,日銷售量150箱的概率為0.1,160箱的概率為0.2,170箱的概率為0.4,180箱的概率為0,3,列表如下:
| 市場銷售狀態(日銷售量) | 概率 | 累計概率值 |
| 150箱 | 0.1 | 1.0 |
| 160箱 | 0.2 | 0.9 |
| 170箱 | 0.4 | 0.7 |
| 180箱 | 0.3 | 0.3 |
本例中客觀自然狀態變數(日銷售量)可以用有序的數量表示,其累積概率按日銷售量由高向低(由180箱向]50箱)累積計算。下麵運用邊際分析方法計算轉折既率:
Mp=700-500=200(元)
Mt=500-200=300(元)
P≥\frac{300}{200+300}≥0.6
根據轉折概率計算期望邊際利潤和期望邊際損失:
期望邊際利潤Mp×P=200×0.6=120(元)
期望邊際損失Mt×(1-p)=300×(1-0.6)=120(元)
將轉折概率與累積概率進行比較,如果能找到與轉折概率相等的累積概率,該累積概率的期望邊際利潤等於期望邊際損失,其所對應的日銷售量就是最佳銷售量。一般情況下找不到與轉折概率相等的累積概率,因此,需按累積概率計算期望邊際利潤和期望邊際損失,按期望邊際利潤大於期望邊際損失的原則選擇方案。根據有關資料計算如下:
| 日銷售量 | 累積概率 | 期望邊際利潤 | 期望邊際損失 |
| 180箱 | 0.3 | 200×0.3=60 | 300×(1-0.3)=210 |
| 170箱 | 0.7 | 200×0.7=140 | 300×(1-0.7)=210 |
| 160箱 | 0.9 | 200×0.9=180 | 300×(1-0.9)=30 |
| 150箱 | 1.0 | 200×1.0=200 | 300×(1-1)=0 |
從上表可以看出,累積概率0.3時,其期望邊際利潤60元小於期望邊際損失210元,不符合選擇的原則。累積概率0.7時,其期望邊際利潤140元大於期望邊際損失90元,以下累積概率期望邊際利潤都大於期望邊際損失。在這些累積概率中應選擇最接近轉折概率的累積概率。本例轉折概率為0.6,最接近的累積改了是0.7,累積概率0.7對應的日銷售量170箱即為應選擇的方案。
用期望值方法對本例進行風險決策,結果與邊際分析方法是一致的。
按最大期望盈利值為32000元,其對應的日銷售量是170箱,與邊際分析方法選擇的結果一致。
邊際分析法主要研究在一定產量水平下,每增加一個產品對總利潤的影響,即:邊際利潤=邊際收人一邊際成本,當邊際收人>邊際成本,則邊際利潤>0,意味著增加單位產量可使總利潤增加,此時企業的產量不是最優;當邊際收人<邊際成本,則邊際利潤<0,意味著減少單位產量可使總利潤增加,此時企業的產量也不是最優。只有當邊際收人=邊際成本時,邊際利潤=0,意味著總利潤達到極大,產量最優。
從邊際分析方法的基本原理來看,邊際分析方法的思路具有這樣幾個特征:
1、不考慮存量資源的情況,側重分析新增一單位要素對整體收益的影響;
2、邊際分析方法是一種動態分析的方法,主要考察要素變化帶來的收益的變化;
3、從決策的角度來看,邊際分析方法實際上強調,決策前最後一個單位的增量資源往往對決策的影響最大。
邊際方法的運用,為電信業務層投資效益評價帶來了新的方法和思路,同時其分析結果,對實際決策也更有指導意義。
1、電信新業務的投資效益前評估。電信網路投資具有規模大、設備專用性高的特征,由於固定投資比重較大,對電信產品成本結構的直接影響是:電信產品的固定成本比重普遍較大,可變成本相對比重較小,通常電信網路在建成之初,網路資源的容量基本可以確定,在達到既定容量之前,每增加一個單位產品/用戶的成本(即邊際成本)都非常低。並且新增加的用戶在享受服務時,對其他用戶的消費活動不產生影響,也不會對網路運營成本產生顯著影響。因此,邊際本低是電信網路投資的一個重要特點,基於這個特點,在進行電信新業務的投資效益預測時,可能在考慮全部成本時,該業務的投資料是完全虧損的。但是,對於已經發生的設備投資和固定成本,實際上都可以視為是一種“沉沒成本”。無論是否開發新業務,這都分成本都已經支出了,邊際效益強調的是總利潤的望乏大化,因此,只要該業務的邊際收氣》邊際成本,對於這類新業務的投資應該就具有可行性。
2、電信滾動性探資的效益後評價。在傳統的投資效益評價過程中、由於電信資金投放的滾動性,在進行投資效益評價時,往往無法清晰地界定存量資金和增量資金的效果。如果要全面地對電信業務的投資效益進行後評價,可以從兩個層面進行分析:第一個層面是就電信業務的整體投資效益進行分析評價,這個整體投資效益的概念主要是從投資評價的期間來看的,整體效益主要是考慮該業務自投資以來至投資評價時點這個時間段內所發生的全部投資、收人和成本情況,通過選取利潤率、已投資本回報率、投資收人比等指標,評測該類業務在整個評價期內的整體效益情況。第二個就是分析該業務的邊際效益情況,考慮到數據提取的便利性和合理性,建議以年度為單位進行邊際效益的測算。所謂邊際效益主要是考察截止到當年年末,當期新增投資、新增收人和新增成本等要素,計算當期的邊際效益指標,如利潤率、已投資本回報率、投資收人比等。這裡的邊際效益指標主要反映的是當期末存量資金和增量資金的綜合效果,其指標含義是當期期末這個時點上存量投資和新增投資的效益狀況。運用該方法對業務連續幾年的邊際效益情況進行分析,就可以畫出該業務的邊際效益變化曲線,從而反映該業務歷年投資、不同時點的效益變化情況。
本条目由以下用户参与贡献
Angle Roh,18°@鷺島,Zfj3000,Vulture,Cabbage,Banxian,Dan,Yixi,泡芙小姐,jane409,KAER,方小莉,Gaoshan2013,寒曦,Lin,Rebecca yin,李庚杰,LuyinT.評論(共24條)
其實就是兩個簡單公式。 一個是求轉折概率P0*Mp=(1-P0)*Mt
另一個是求收益最大Max存量=C+[P0/(p1-p<-1>)]*[C<P1>-C
] 結果只講了一個公式還講得雲山霧罩,第二個公式壓根沒講 跟我大學老師一個水平 學經濟的都是這弔樣,簡單問題給你吹得玄玄乎乎 不好意思,學經濟的也不都是這弔樣,我也是學經濟的
第二個公式被吞了好幾個字母。。。。重新發:
收益最大Max存量=C<-1>+[(P<1>-P0)/(p1-p<-1>)]*[C<P1>-C]
]
問一下啊,邊際分析,當邊際收入和邊際支出為零時利潤最大化,收入和支出都為零了,意義何在








好文章,很久沒有看到這麼精彩的、立意點這麼高的評論了。那一種海納百川、從容若定、胸中自有丘壑的氣度,令人佩服!