曲線擬合

出自 MBA智库百科(https://wiki.mbalib.com/)

曲線擬合(Curve Fitting)

　　曲線擬合是指用連續曲線近似地刻畫或比擬平面上離散點組所表示的坐標之間的函數關係。推求一個解析函數y=f(x)使其通過或近似通過有限序列的資料點(xi，yi)，通常用多項式函數通過最小二乘法求得此擬合函數。

　　用連續曲線近似地刻畫或比擬平面上離散點組所表示的坐標之間的函數關係。更廣泛地說，空間或高維空間中的相應問題亦屬此範疇。在數值分析中，曲線擬合就是用解析表達式逼近離散數據，即離散數據的公式化。實踐中，離散點組或數據往往是各種物理問題和統計問題有關量的多次觀測值或實驗值，它們是零散的，不僅不便於處理，而且通常不能確切和充分地體現出其固有的規律。這種缺陷正可由適當的解析表達式來彌補。

　　(x_k,y_k) (k=1,2,…,m),(1)

　　式中x_k為自變數x(標量或向量,即一元或多元變數)的取值；y_k為因變數 y（標量）的相應值。曲線擬合要解決的問題是尋求與(1)的背景規律相適應解析表達式

　　y=f(x,b),(2)

　　使它在某種意義下最佳地逼近或擬合(1),?(x,b)稱為擬合模型；為待定參數,當b)僅在?中線性地出現時，稱模型為線性的，否則為非線性的。量

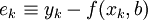　　(k=1,2,…，m)

　　稱為在x_k處擬合的殘差或剩餘，衡量擬合優度的標準通常有

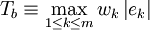　　 或

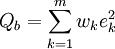
　　式中ωk>0為權繫數或權重（如無特別指定，一般取為平均權重，即w_k(k=1,2,…,m),此時無需提到權）。當參數b)使T(b))或Q(b))達到最小時，相應的(2)分別稱為在加權切比雪夫意義或加權最小二乘意義下對 (1)的擬合，後者在計算上較簡便且最為常用。

　　模型中參數的確定 　一般的線性模型是以參數 b)為繫數的廣義多項式，即

　　f(x,b)=b₀g₀(x)+b₁g₁(x)+…b_ng_n(x)　　　 (3)

　　式中g0,g1,…，gn稱為基函數。對諸gj的不同選取可構成多種典型的和常用的線性模型。從函數逼近的觀點來看，式(3)還能近似地體現許多非線性模型的性質。

　　在最小二乘意義下用線性模型(3)擬合離散點組(1)，參數b可通過解方程組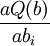=0(i=0,…,n)來確定，即解關於b0,b1,…,bn的線性代數方程組

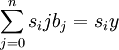　　(i=0,1,…，n),　　　(4)

　　式中　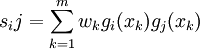　　 　 (i,j＝0,1,…，n),

　　方程組(4)通常稱為法方程或正規方程，當m>n時一般有惟一解。

　　至於非線性模型以及非最小二乘原則的情形,參數b)可通過解非線性方程組或最優化計算中的有關方法來確定（見非線性方程組數值解法、最優化）。

　　對於給定的離散數據(1),需恰當地選取一般模型(2)中函數f(x,b)的類別和具體形式,這是擬合效果的基礎。若已知(1)的實際背景規律，即因變數y對自變數 x的依賴關係已有表達式形式確定的經驗公式，則直接取相應的經驗公式為擬合模型。反之，可通過對模型(3)中基函數g0,g1,…,gn(個數和種類)的不同選取，分別進行相應的擬合併擇其效果佳者。函數g0,g1,…,gn對模型的適應性起著測試的作用，故又稱為測試函數。另一種途徑是:在模型(3)中納入個數和種類足夠多的測試函數，藉助於數理統計方法中的相關性分析和顯著性檢驗，對所包含的測試函數逐個或依次進行篩選以建立較適合的模型（見回歸分析）。當然，上述方法還可對擬合的殘差（視為新的離散數據）再次進行，以彌補初次擬合的不足。總之，當數據中變數之間的內在聯繫不明確時，為選擇到相適應的模型，一般需要反覆地進行擬合試驗和分析鑒別。