組數

出自 MBA智库百科(https://wiki.mbalib.com/)

　　組數是指一群數據分組的數目，用k表示。

　　組數的多少直接取決於兩個因素：一個是總體的全距，另一個是組距。

　　全距是總體中最大的標誌值與最小的標誌值之差。在等距分組的條件下，組數等於全距除以組距。在組距既定的條件下，全距大則組數多，全距小則組數少；在全距既定的條件下，組距大則組數少，組距小則組數多。

　　決定組數的多少，並無規則可言，必須憑藉經驗和所研究問題的性質作出判斷。

　　一組數據分多少組合適呢？一般與數據本身的特點及數據的多少有關。由於分組的目的之一是為了觀察數據分佈的特征，因此組數的多少應適中。如組數太少，數據的分佈就會過於集中，組數太多，數據的分佈就會過於分散，這都不便於觀察數據分佈的特征和規律。組數的確定應以能夠顯示數據的分佈特征和規律為目的。在實際分組時，可以按斯特奇斯（Sturges）提出的經驗公式來確定組數K：

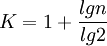
　　其中n為數據的個數，對結果用四捨五入的辦法取整數即為組數。例如，對前例的數據有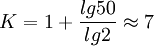：，即應分為7組。當然，這隻是一個經驗公式，實際應用時，可根據數據的多少和特點及分析的要求，參考這一標準靈活確定組數。