顯著性檢驗
出自 MBA智库百科(https://wiki.mbalib.com/)
顯著性檢驗(Significance Testing)
目錄 |
顯著性檢驗就是事先對總體(隨機變數)的參數或總體分佈形式做出一個假設,然後利用樣本信息來判斷這個假設(原假設)是否合理,即判斷總體的真實情況與原假設是否顯著地有差異。或者說,顯著性檢驗要判斷樣本與我們對總體所做的假設之間的差異是純屬機會變異,還是由我們所做的假設與總體真實情況之間不一致所引起的。
顯著性檢驗是針對我們對總體所做的假設做檢驗,其原理就是“小概率事件實際不可能性原理”來接受或否定假設。
抽樣實驗會產生抽樣誤差,對實驗資料進行比較分析時,不能僅憑兩個結果(平均數或率)的不同就作出結論,而是要進行統計學分析,鑒別出兩者差異是抽樣誤差引起的,還是由特定的實驗處理引起的。
顯著性檢驗即用於實驗處理組與對照組或兩種不同處理的效應之間是否有差異,以及這種差異是否顯著的方法。
常把一個要檢驗的假設記作H0,稱為原假設(或零假設) (null hypothesis) ,與H0對立的假設記作H1,稱為備擇假設(alternative hypothesis) 。
⑴ 在原假設為真時,決定放棄原假設,稱為第一類錯誤,其出現的概率通常記作α;
⑵ 在原假設不真時,決定接受原假設,稱為第二類錯誤,其出現的概率通常記作β。
通常只限定犯第一類錯誤的最大概率α, 不考慮犯第二類錯誤的概率β。這樣的假設 檢驗又稱為顯著性檢驗,概率α稱為顯著性水平。
最常用的α值為0.01、0.05、0.10等。一般情況下,根據研究的問題,如果放棄真錯誤損失大,為減少這類錯誤,α取值小些 ,反之,α取值大些。
- 無效假設
顯著性檢驗的基本原理是提出“無效假設”和檢驗“無效假設”成立的機率(P)水平的選擇。所謂“無效假設”,就是當比較實驗處理組與對照組的結果時,假設兩組結果間差異不顯著,即實驗處理對結果沒有影響或無效。經統計學分析後,如發現兩組間差異系抽樣引起的,則“無效假設”成立,可認為這種差異為不顯著(即實驗處理無效)。若兩組間差異不是由抽樣引起的,則“無效假設”不成立,可認為這種差異是顯著的(即實驗處理有效)。
- “無效假設”成立的機率水平
檢驗“無效假設”成立的機率水平一般定為5%(常寫為p≤0.05),其含義是將同一實驗重覆100次,兩者結果間的差異有5次以上是由抽樣誤差造成的,則“無效假設”成立,可認為兩組間的差異為不顯著,常記為p>0.05。若兩者結果間的差異5次以下是由抽樣誤差造成的,則“無效假設”不成立,可認為兩組間的差異為顯著,常記為p≤0.05。如果p≤0.01,則認為兩組間的差異為非常顯著。
1、原假設:對總體所作的論斷或推測,指觀察到的差異只反映機會變異。記作H0。
2、備擇假設:是指觀察到的差異是真實的。記作H1。
3、原假設和備擇假設合在一起,應涵蓋我們所研究的總體特征的所有可能性。
採用雙尾檢驗還是採用單尾檢驗(以及左單尾還是右單尾),取決於備擇假設的形式。
表1:拒絕域的單、雙尾與備擇假設之間的對應關係
| 拒絕域位置 | 原假設 | 備擇假設 |
|---|---|---|
| 雙尾 | H0:θ = θ0 | 
|
| 左單尾 |  (不可能有θ > θ0時,H0:θ = θ0) (不可能有θ > θ0時,H0:θ = θ0) | H1:θ < θ0 |
| 右單尾 | 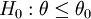 (不可能有θ < θ0時,H0:θ = θ0) (不可能有θ < θ0時,H0:θ = θ0) | H1:θ > θ0 |
分析工作者常常用標準方法與自己所用的分析方法進行對照試驗,然後用統計學方法檢驗兩種結果是否存在顯著性差異。若存在顯著性差異而又肯定測定過程中沒有錯誤,可以認定自己所用的方法有不完善之處,即存在較大的系統誤差。
因此分析結果的差異需進行統計檢驗或顯著性檢驗。
顯著性檢驗的基本思想可以用小概率原理來解釋。
1、小概率原理:小概率事件在一次試驗中是幾乎不可能發生的,假若在一次試驗中事件 事實上發生了。那隻能認為事件 不是來自我們假設的總體,也就是認為我們對總體所做的假設不正確。
2、觀察到的顯著水平:由樣本資料計算出來的檢驗統計量觀察值所截取的尾部面積為。這個概率越小,反對原假設,認為觀察到的差異表明真實的差異存在的證據便越強,觀察到的差異便越加理由充分地表明真實差異存在。
3、檢驗所用的顯著水平:針對具體問題的具體特點,事先規定這個檢驗標準。
4、在檢驗的操作中,把觀察到的顯著性水平與作為檢驗標準的顯著水平標準比較,小於這個標準時,得到了拒絕原假設的證據,認為樣本數據表明瞭真實差異存在。大於這個標準時,拒絕原假設的證據不足,認為樣本數據不足以表明真實差異存在。
5、檢驗的操作可以用稍許簡便一點的作法:根據所提出的顯著水平查表得到相應的 值,稱作臨界值,直接用檢驗統計量的觀察值與臨界值作比較,觀察值落在臨界值所劃定的尾部內,便拒絕原假設;觀察值落在臨界值所劃定的尾部之外,則認為拒絕原假設的證據不足。
1、顯著性檢驗中的第一類錯誤及其概率
顯著性檢驗中的第一類錯誤是指,原假設H0:θ = θ0事實上正確,可是檢驗統計量的觀察值卻落入拒絕域,因而否定了本來正確的假設。這是棄真的錯誤。
發生第一類錯誤的概率(記作 )也就是當原假設H0:θ = θ0正確時檢驗統計量的觀察值落入拒絕域的概率。顯然,在雙尾檢驗時是兩個尾部的拒絕域面積之和;在單尾檢驗時是單尾拒絕域的面積。
2、顯著性檢驗中的第二類錯誤及其概率
顯著性檢驗中的第二類錯誤是指,原假設H0:θ = θ0不正確,而備擇假設H1:θ < θ0或H1:θ > θ0是正確的,可是檢驗統計量的觀察值卻落入了接受域,因而沒有否定本來不正確的原假設。這是取偽的錯誤。
發生第二類錯誤的概率(記作 )是指,把來自 的總體的樣本值代入檢驗統計量所得結果落入接受域的概率。
的總體的樣本值代入檢驗統計量所得結果落入接受域的概率。
- 3、α和β的關係
當樣本容量一定時,α越小,β就越大;反之,α越大,β就越小。
顯著性檢驗的P值[1]
若用電腦統計軟體進行假設檢驗, 我們會見到P—值。將算得檢驗統計量樣本值查表得的概率是就是P值(在那裡我們稱之為觀察到的顯著水平)。
P值是怎麼來的
從某總體中抽樣所得的樣本,其參數會與總體參數有所不同,這可能是由於兩種原因:
⑴、這一樣本是由該總體抽出,其差別是由抽樣誤差所致;
⑵、這一樣本不是從該總體抽出,所以有所不同。
如何判斷是那種原因呢?統計學中用顯著性檢驗賴判斷。其步驟是:
⑴、建立檢驗假設(又稱無效假設,符號為H0):如要比較A藥和B藥的療效是否相等,則假設兩組樣本來自同一總體,即A藥的總體療效和B藥相等,差別僅由抽樣誤差引起的碰巧出現的。
⑵、選擇適當的統計方法計算H0成立的可能性即概率有多大,概率用P值表示。
⑶、根據選定的顯著性水平(0.05或0.01),決定接受還是拒絕H0。
如果P>0.05,不能否定“差別由抽樣誤差引起”,則接受H0;如果P<0.05或P <0.01,可以認為差別不由抽樣誤差引起,可以拒絕H0,則可以接受另一種可能性的假設(又稱備選假設,符號為H1),即兩樣本來自不同的總體,所以兩藥療效有差別。
統計學上規定的P值意義見下表
P值 碰巧的概率 對無效假設 統計意義 P>0.05 碰巧出現的可能性大於5% 不能否定無效假設 兩組差別無顯著意義 P<0.05 碰巧出現的可能性小於5% 可以否定無效假設 兩組差別有顯著意義 P <0.01 碰巧出現的可能性小於1% 可以否定無效假設 兩者差別有非常顯著意義
- 理解P值,下述幾點必須註意:
⑴P的意義不表示兩組差別的大小,P反映兩組差別有無統計學意義,並不表示差別大小。因此,與對照組相比,C藥取得P<0.05,D藥取得P <0.01並不表示D的藥效比C強。
⑵ P>0.05時,差異無顯著意義,根據統計學原理可知,不能否認無效假設,但並不認為無效假設肯定成立。在藥效統計分析中,更不表示兩藥等效。哪種將“兩組差別無顯著意義”與“兩組基本等效”相同的做法是缺乏統計學依據的。
⑶統計學主要用上述三種P值表示,也可以計算出確切的P值,有人用P <0.001,無此必要。
⑷顯著性檢驗只是統計結論。判斷差別還要根據專業知識。
關於顯著性檢驗的結果:
(一)顯著性檢驗回答什麼問題
我們所觀察到的差異(是純屬於機會變異,還是反映了真實的差異?
1、如果顯著性檢驗得到差異顯著的結論這時並不能評價差異的大小和重要性。
2、顯著性檢驗只能告訴我們差異是否在事實上存在,而不能回答差異產生的原因。
3、顯著性檢驗不能檢查我們對實驗所作的設計是否有缺陷
(二)顯著性檢驗回答問題的方式
在表述顯著性檢驗結論的時候,應與檢驗的邏輯推理相符。
當檢驗統計量的觀察值落在拒絕域時,我們應該說,樣本資料顯著地(或高度顯著地)表明,差異是存在的。
(三)對觀察到的顯著水平數值的評價
1、顯著性檢驗的對象是無限總體。
2、大樣本可能會使檢驗統計量過分敏感。
3、從有限總體中抽取樣本用於顯著性檢驗時,必須作概率抽樣。
顯著性檢驗的一般步驟或格式,如下:
1、提出假設
H0:______
H1:______
同時,與備擇假設相應,指出所作檢驗為雙尾檢驗還是左單尾或右單尾檢驗。
2、構造檢驗統計量,收集樣本數據,計算檢驗統計量的樣本觀察值。
3、根據所提出的顯著水平 ,確定臨界值和拒絕域。
4、作出檢驗決策。
把檢驗統計量的樣本觀察值和臨界值比較,或者把觀察到的顯著水平與顯著水平標準比較;最後按檢驗規則作出檢驗決策。當樣本值落入拒絕域時,表述成:“拒絕原假設”,“顯著表明真實的差異存在”;當樣本值落入接受域時,表述成:“沒有充足的理由拒絕原假設”,“沒有充足的理由表明真實的差異存在”。另外,在表述結論之後應當註明所用的顯著水平。
總體均值的顯著性檢驗可有雙尾、左單尾、右單尾三種不同的情況。下麵就總體分佈的不同情況,總體方差是否已知的不同情況以及樣本大小的不同情況分別介紹檢驗統計量和檢驗規則。
一、總體為正態分佈,總體方差已知,樣本不論大小
對於假設:H0:μ = μ0,在H0成立的前提下,有檢驗統計量

如果規定顯著性水平為 ,在雙尾,左單尾,右單尾三種不同情形下,拒絕域分別為:① ![(-\infty,-z_{a/2}]](/w/images/math/4/b/9/4b92019482108a5cc17f099fad231082.png) 和
和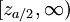 ;②
;②![(-\infty,-z_a]](/w/images/math/4/2/3/423a4284894055c83f7ce337aa653f8a.png) ;③
;③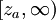 。
。
二、總體分佈未知,總體方差已知,大樣本
對於假設H0:μ = μ0,在H0成立的前提下,如果樣本足夠大(n≥30),近似地有檢驗統計量

如果規定顯著性水平為a,在雙尾,左單尾,右單尾三種不同情形下,拒絕域分別為①![(-\infty,-z_{a/2}]](/w/images/math/4/b/9/4b92019482108a5cc17f099fad231082.png) 和
和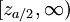 ;②
;②![(-\infty,-z_a]](/w/images/math/4/2/3/423a4284894055c83f7ce337aa653f8a.png) ;③
;③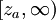 。
。
三、總體為正態分佈,總體方差未知,小樣本
對於假設H0:μ = μ0,在H0成立的前提下,有檢驗統計量
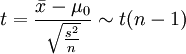
如果規定顯著性水平為a,在雙尾,左單尾,右單尾三種不同情形下,拒絕域分別為:①![(-\infty,-t_{a/2}(n-1)]](/w/images/math/6/4/c/64cd167372b41bd8fe1cdbf88a32bb93.png) 和
和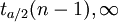 ;②
;②![(-\infty,-t_a(n-1)]](/w/images/math/d/e/0/de0490e649152f6502bdfec3050d1b97.png) ;③
;③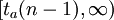 。
。
四、總體分佈未知,總體方差未知,大樣本
對於假設H0:μ = μ0,在H0成立的前提下,如果總體偏斜適度,且樣本足夠大,近似地有檢驗統計量
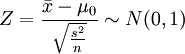
如果規定顯著性水平為a,在雙尾,左單尾,右單尾三種不同情形下,拒絕域分別為:① ![(-\infty,-z_{a/2}]](/w/images/math/4/b/9/4b92019482108a5cc17f099fad231082.png) 和
和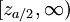 ; ②
; ②![(-\infty,-z_{a}]](/w/images/math/9/4/3/943a26a261665c122abadb161d90ecab.png) ;③
;③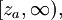
總體比例指的是隨機試驗中某種指定事件出現的概率。隨機試驗中某種指定事件出現叫做“成功”,把一次試驗中成功的概率記作π。
對於假設H0:π = π0,在H0成立的前提下,如果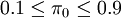 ,並且樣本容量足夠大,大到足以滿足
,並且樣本容量足夠大,大到足以滿足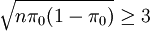 時,近似地有檢驗統計量
時,近似地有檢驗統計量
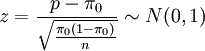
其中p是樣本比例。
如果規定顯著性水平為a,在雙尾,左單尾,右單尾三種不同情形下,拒絕域分別為:
① ![(-\infty,-z_{a/2}]](/w/images/math/4/b/9/4b92019482108a5cc17f099fad231082.png) 和
和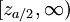 ;②
;②![(-\infty,-z_a]](/w/images/math/4/2/3/423a4284894055c83f7ce337aa653f8a.png) ;③
;③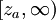 。
。
進行顯著性檢驗還應註意以下幾個問題:
1、要有合理的試驗設計和準確的試驗操作,避免系統誤差、降低試驗誤差,提高試驗的準確性和精確性。
2、選用的顯著性檢驗方法要符合其應用條件。由於研究變數的類型、問題的性質、條件、試驗設計方法、樣本大小等的不同,所選用的顯著性檢驗方法也不同,因而在選用檢驗方法時,應認真考慮其應用條件和適用範圍。
3、選用合理的統計假設。進行顯著性檢驗時,無效假設和備擇假設的選用,決定了採用兩尾檢驗或是一尾檢驗。 4、正確理解顯著性檢驗結論的統計意義。顯著性檢驗結論中的“差異顯著”或“差異極顯著”不應該誤解為相差很大或非常大,也不能認為在實際應用上一定就有重要或很重要的價值。“顯著”或“極顯著”是指錶面差異為試驗誤差可能性小於0.05或0.01,已達到了可以認為存在真實差異的顯著水平。有些試驗結果雖然錶面差異大,但由於試驗誤差大,也許還不能得出“差異顯著”的結論,而有些試驗的結果雖然錶面差異小,但由於試驗誤差小,反而可能推斷為“差異顯著”。
顯著水平的高低只表示下結論的可靠程度的高低,即在0.01水平下否定無效假設的可靠程度為99%,而在0.05水平下否定無效假設的可靠程度為95%。
“差異不顯著”是指錶面差異為試驗誤差可能性大於統計上公認的概率水平0.05,不能理解為沒有差異。下“差異不顯著”的結論時,客觀上存在兩種可能:一是無本質差異,二是有本質差異,但被試驗誤差所掩蓋,表現不出差異的顯著性來。如果減小試驗誤差或增大樣本容量,則可能表現出差異顯著性。顯著性檢驗只是用來確定無效假設能否被否定,而不能證明無效假設是正確的。
5、統計分析結論的應用,還要與經濟效益等結合起來綜合考慮。
1.t檢驗
適用於計量資料、正態分佈、方差具有齊性的兩組間小樣本比較。包括配對資料間、樣本與均數間、兩樣本均數間比較三種,三者的計算公式不能混淆。
2.t'檢驗
應用條件與t檢驗大致相同,但t′檢驗用於兩組間方差不齊時,t′檢驗的計算公式實際上是方差不齊時t檢驗的校正公式。
3.U檢驗
應用條件與t檢驗基本一致,只是當大樣本時用U檢驗,而小樣本時則用t檢驗,t檢驗可以代替U檢驗。
4.方差分析
用於正態分佈、方差齊性的多組間計量比較。常見的有單因素分組的多樣本均數比較及雙因素分組的多個樣本均數的比較,方差分析首先是比較各組間總的差異,如總差異有顯著性,再進行組間的兩兩比較,組間比較用q檢驗或LST檢驗等。
5.X2檢驗
是計數資料主要的顯著性檢驗方法。用於兩個或多個百分比(率)的比較。常見以下幾種情況:四格表資料、配對資料、多於2行*2列資料及組內分組X2檢驗。
6.零反應檢驗
用於計數資料。是當實驗組或對照組中出現概率為0或100%時,X2檢驗的一種特殊形式。屬於直接概率計演算法。
三者均屬非參數統計方法,共同特點是簡便、快捷、實用。可用於各種非正態分佈的資料、未知分佈資料及半定量資料的分析。其主要缺點是容易丟失數據中包含的信息。所以凡是正態分佈或可通過數據轉換成正態分佈者儘量不用這些方法。
用於計量資料、正態分佈、兩組間多項指標的綜合差異顯著性檢驗。
顯著性檢驗的應用[2]
在市場調研中,由於人力、物力、時間等問題,一般都用抽樣調查的方法抽取一定數量的具有代表性的群體,得出樣本數據來進行市場研究,並對市場總體特征進行統計推斷,在這裡面就會存在兩個問題,一是樣本的特征數量能否反映總體特征?二是,兩種不同的樣本的數量標誌參數是否存在差異?只有解決這兩個問題,才能正確的推斷市場總體特征,也才能找出市場中不同特征群體的需求差異,這就需要統計學中的顯著性檢驗來解決,由於顯著性檢驗的功能在數據分析中的重大作用,顯著性檢驗在市場調研中得到了廣泛的應用;但若不恰當的使用便會導致市場調研信息反應的歪曲或挖掘不充分;以下是我根據以往應用顯著性檢驗的經驗而總結的一些關於如何恰當的應用統計檢驗的體會,僅供參考、討論。
要恰當的運用檢驗方法,我們需要做到以下幾點:
首先,瞭解各檢驗方法的適用範圍及其特點。
這也是正確使用檢驗方法的基本前提,只有瞭解各檢驗方法的基本思想及特點,才能正確選取適當的檢驗方法。
許多統計檢驗方法的應用對總體有特殊的要求,如t檢驗要求總體符合正態分佈,F檢驗要求誤差呈正態分佈且各組方差整齊,等等。這些常用來估計或檢驗總體參數的方法,統稱為參數統計。許多調查或實驗所得的科研數據,其總體分佈未知或無法確定,這時做統計分析常常不是針對總體參數,而是針對總體的某些一般性假設(如總體分佈),這類方法稱非參數統計,相應的,統計檢驗總體分為參數檢驗和非參數檢驗。在選擇參數與非參數檢驗時,首要考慮是數據的分佈情況,能確定分佈類型的,則可適當選用參數檢驗,參數檢驗主要包括包含的方法有:單樣本T檢驗、兩獨立樣本T檢驗、兩配對樣本T檢驗;非參數由於不限制分佈,統計方法簡便,適用性強,但檢驗效率較低,應用時應適當加以考慮,非參數檢驗主要涉及五個方面,即單樣本、兩獨立樣本、兩配對樣本、多獨立樣本、多配對樣本的非參數檢驗。
不同的檢驗方法,比較的統計量是不同的。T檢驗等檢驗方法都是比較的均值;卡方檢驗、K-S檢驗等比較頻數;曼-惠特尼U檢驗等是對秩進行比較;符號檢驗法比較的是前後變化差值的符號、而符號秩檢驗法則是對差值及符號一同比較的檢驗。
其次,認清研究目的。
研究目的是市場調研中一切實務的根本出發點,做數據分析時同樣首要考慮的是研究目的,研究目的也是數據分析的方向,但此時研究目的需要細化,具體到要通過哪些數據、得到什麼信息、何種結果的問題,如希望通過對消費者購買哪些品牌的數據來得出市場占有率的信息。
再次,分析數據特點。
明確某些數據的研究目的後,需要認清數據自身特點。第一,弄清楚要分析的數據屬於什麼類型,是連續型,還是非連續型?對於連續型數值,均值具有實際意義,對於非連續性的數值,均值並不具備實際意義,而是頻數,百分比才有意義,所以,數據屬於連續型時,適用比較均值的顯著性檢驗,若是非連續型的級數類,則適用比較頻數、比例的檢驗方法;其實,數據也是可以跟據不同情況,靈活處理的,如對於滿意度的衡量,我們可以根據不同的需求看為連續型分值,也可以看為幾個等級的級數;第二,我們還需要瞭解樣本數據的分佈特點,弄清楚樣本數據是否服從某一分佈,對於分佈明確的,可以採用參數檢驗,而不清楚分佈情況的則可以採用非參數檢驗法;第三,判斷要檢驗差異的兩組樣本的關係,屬於獨立樣本,還是屬於配對樣本。獨立樣本即指在一個總體中隨機抽樣對在另一個總體中隨機抽樣沒有影響的情況下所獲得的樣本,樣本之間相互獨立;而配對樣本可以是同一個體在前後兩種狀態下某種屬性的兩種狀態,也可以是對某事物兩個不同側面或方面的描述,兩樣本不是相互獨立,而是有相關性的。
最後,靈活運用檢驗方法。
檢驗方法雖然有各自特點和適用範圍,但是可以對數據做稍微的處理、變化,或是換個角度分析,便可運用不同的檢驗方法;且各方法有適用範圍,當然也有它的局限性,有時需要多種檢驗方法配合使用,相互補充,才能充分的挖掘信息,比如,獨立樣本T檢驗法判斷AB產品對於抗過敏的功效評價在均值上是否有差異,而卡方檢驗可判斷他們在各評價水平上的分佈有無差異,假如判斷出他們功效水平無差異之後,我們還想知道他們到底是同樣的好還是同樣的差,這時可以再使用單樣本 T 檢驗對以與均值評價水平相近的滿意度水平進行差異性檢驗來進行定位。 此外,我們還需要合理解釋檢驗結果。
不僅要正確識別檢驗結果,還需要結合原始數據及實際意義,並針對研究目的來分析說明。
例如,目前我國大豆育種工作者認為,大豆籽粒蛋白質含量高於45%(記為μ0)的品種為高蛋白品種。某種子公司對一大豆新品種隨機抽取5個樣品進行測定,得平均蛋白質含量為 ,
, 。我們能否根據
。我們能否根據 就認定該大豆新品種就是高蛋白品種?結論是,不一定。
就認定該大豆新品種就是高蛋白品種?結論是,不一定。
因為通過5個樣品測定的蛋白質含量計算的樣本平均數 僅是該大豆品種蛋白質含量總體平均數μ的一個估計值。由於存在抽樣誤差,任何一個樣品測定值xi,都可以表示為
僅是該大豆品種蛋白質含量總體平均數μ的一個估計值。由於存在抽樣誤差,任何一個樣品測定值xi,都可以表示為
xi = μ + εi (i=1,2,…,n) (1)
其中,μ為總體平均數,εi為抽樣誤差。
樣本平均數 為
為
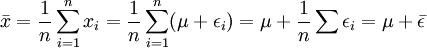 (2)
(2)
(1)式表明,樣本平均數 包含了總體平均數μ與抽樣誤差
包含了總體平均數μ與抽樣誤差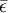 二部分。
於是,
二部分。
於是,
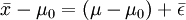 (3)
(3)
(2)式表明, 是由兩部分組成:一部分是兩總體平均數的真實差異(μ − μ0);另一部分是抽樣誤差
是由兩部分組成:一部分是兩總體平均數的真實差異(μ − μ0);另一部分是抽樣誤差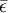 。
。 並不能代表新品種蛋白質含量總體平均數μ與標準含量μ0之間的真實差異,我們稱
並不能代表新品種蛋白質含量總體平均數μ與標準含量μ0之間的真實差異,我們稱 為錶面差異。雖然真實差異(μ − μ0)未知,但錶面差異
為錶面差異。雖然真實差異(μ − μ0)未知,但錶面差異 是可以計算的,藉助數理統計方法可以對試驗誤差作出估計。所以,可將錶面差異
是可以計算的,藉助數理統計方法可以對試驗誤差作出估計。所以,可將錶面差異 與試驗誤差相比較間接推斷真實差異μ − μ0是否存在,這就是差異顯著性檢驗的基本思想。顯著性檢驗的目的在於判明,錶面差異
與試驗誤差相比較間接推斷真實差異μ − μ0是否存在,這就是差異顯著性檢驗的基本思想。顯著性檢驗的目的在於判明,錶面差異 主要是由真實差異μ − μ0造成的,還是由抽樣誤差
主要是由真實差異μ − μ0造成的,還是由抽樣誤差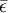 造成的,從而得到可靠的結論。
造成的,從而得到可靠的結論。
案例二:信用評級對企業債券市場定價影響力的判斷[3]
一、模型設計
選取2008年、2009年和2010年發行的企業債券為研究樣本,根據以下原則進行分組:(1)期限結構相同的兩組企業債券(A1、A2)在同一月度內發行,且該兩組企業債券的債項評級和主體評級均相同,命名為樣本組A,得到有效樣本67個;(2)期限結構相同的兩組企業債券(B1、B2)在同一月度內發行,且其中一組企業債券(B2)的債項評級和主體評級均優於另一組(B1),命名為樣本組B,得到有效樣本76個;(3)期限結構完全相同的兩組企業債券(C1、C2)在同一月度內發行,且該兩組企業債券的債項評級相同,主體評級不同,命名為樣本組C,得到有效樣本58個;(4)期限結構完全相同的兩組企業債券(D1、D2)在同一月內發行,且該兩組企業債券的主體評級相同,債項評級不同,命名為樣本組D,得到有效樣本49個。
計量經濟理論中,用來比較兩組數據是否存在顯著性差異的方法是t檢驗。本文采用配對設計兩樣本均數差異顯著性檢驗的方法來驗證A1與A2、B1與B2、C1與C2、D1與D2是否存在顯著性差異。所採用的研究樣本之所以選取期限結構完全相同而且是在同一個月內發行的兩組債券作為配對樣本,原因在於只有期限結構完全相同的債券其發行利差的比較才有意義,在同一個月內發行也大大減少了市場上資金供求關係對債券發行利差造成的影響,因此,本文將企業債券在同一月度內發行視為在同一時期發行。
二、實證分析
採用excel 2007對樣本數據進行分析,顯著性水平取0.05。根據顯著性檢驗的計量經濟理論,運用t檢驗法檢驗兩組數據是否存在顯著性差異時,對樣本數據要求方差齊性,即各組資料的總體方差相等。因此,在對各組樣本數據進行t檢驗之前,先要對各組樣本數據進行方差齊性檢驗,一般採用F檢驗來完成。
(一)F檢驗
首先對樣本數據組A1與A2、Bl與B2、C1與C2、D1與D2用excel 2007進行方差齊性檢驗(F檢驗),計量結果如表1至表4所示。
表1 A1、A2的方差齊性檢驗(F檢驗)
| 項目\分類 | A1 | A2 |
|---|---|---|
| 平均 | 3.380997 | 3.450907 |
| 方差 | 0.890546 | 0.88167 |
| 觀測值 | 67 | 67 |
| df | 66 | 66 |
| F | 1.010068 | |
| P(F<=f)單尾 | 0.483833 | |
| F單尾臨界 | 1.503607 |
表2 B1、B2的方差齊性檢驗(F檢驗)
| 項目\分類 | B1 | B2 |
|---|---|---|
| 平均 | 3.693077 | 2.834852 |
| 方差 | 1.275205 | 0.963889 |
| 觀測值 | 76 | 76 |
| df | 75 | 75 |
| F | 1.322979 | |
| P(F<=f)單尾 | 0.113918 | |
| F單尾臨界 | 1.465625 |
表3 C1、C2的方差齊性檢驗(F檢驗)
| 項目\分類 | 變數1 | 變數2 |
|---|---|---|
| 平均 | 3.292207 | 3.347521 |
| 方差 | 1.129063 | 1.159825 |
| 觀測值 | 58 | 58 |
| df | 57 | 57 |
| F | 0.973477 | |
| P(F<=f)單尾 | 0.459764 | |
| F單尾臨界 | 0.644431 |
表4 D1、D2的方差齊性檢驗(F檢驗)
| 項目\分類 | 變數1 | 變數2 |
|---|---|---|
| 平均 | 3.190006 | 3.392693 |
| 方差 | 0.931489 | 0.885317 |
| 觀測值 | 49 | 49 |
| df | 48 | 48 |
| F | 1.052153 | |
| P(F<=f)單尾 | 0.430467 | |
| F單尾臨界 | 1.61537 |
考察表1至表4中F檢驗的計量結果,由於各表中P值分別等於0.483 833(表1)、0.113 918(表2)、0.459 764(表3)、0.430 467(表4),均大於0.05,所以,樣本數據組A1與A2、BI與B2、C1與C2、D1與D2各兩組數據的方差是齊性的,即各兩組數據的方差不存在顯著性差異,可以進行t檢驗。
(二)t檢驗
本節對樣本數據組A1與A2、B1與B2、C1與C2、D1與D2用excel 2007進行配對雙樣本的均值分析(t檢驗),計量結果如表5至表8所示。
表5 A1、A2均值分析(t檢驗)
| 項目\分類 | A1 | A2 |
|---|---|---|
| 平均 | 3.380997 | 3.450907 |
| 方差 | 0.890546 | 0.88167 |
| 觀測值 | 67 | 67 |
| 泊松相關係數 | 0.703808 | |
| 假設平均差 | 0 | |
| df | 66 | |
| t Stat | -0.78982 | |
| P(T<=t)單尾 | O.21623 | |
| t單尾臨界 | 1.668271 | |
| P(T<=t)雙尾 | 0.432459 | |
| t雙尾臨界 | 1.996564 |
表6 B1、B2均值分析(t檢驗)
| 項目\分類 | B1 | B2 |
|---|---|---|
| 平均 | 3.693077 | 2.834852 |
| 方差 | 1.275205 | 0.963889 |
| 觀測值 | 76 | 76 |
| 泊松相關係數 | 0.795185 | |
| 假設平均差 | 0 | |
| df | 75 | |
| t Star | 10.84559 | |
| P(T<=t)單尾 | 2.53E-17 | |
| t單尾臨界 | 1.665425 | |
| P(T<=t)雙尾 | 5.06E-17 | |
| t雙尾臨界 | 1.992102 |
表7 C1、C2均值分析(t檢驗)
| 項目\分類 | C1 | C2 |
|---|---|---|
| 平均 | 3.292207 | 3.34752l |
| 方差 | 1.129063 | 1.159825 |
| 觀測值 | 58 | 58 |
| 泊松相關係數 | 0.637837 | |
| 假設平均差 | 0 | |
| df | 57 | |
| t Stat | 1.046265 | |
| P(T<=t)單尾 | 0.322688 | |
| t單尾臨界 | 1.672029 | |
| P(T<=t)雙尾 | 0.645376 | |
| t雙尾臨界 | 2.002465 |
表8 D1、D2均值分析(t檢驗)
| 項目\分類 | D1 | D2 |
|---|---|---|
| 平均 | 3.190006 | 3.392693 |
| 方差 | 0.931489 | 0.885317 |
| 觀測值 | 49 | 49 |
| 泊松相關係數 | 0.588482 | |
| 假設平均差 | 0 | |
| df | 48 | |
| t Stat | -1.6405 | |
| P(T<=t)單尾 | 0.05372 | |
| t單尾臨界 | 1.677224 | |
| P(T<=t)雙尾 | 0.10744 | |
| t雙尾臨界 | 2.010635 |
考察表5至表8中t檢驗的計量結果,表5、表7、表8中P(單尾)分別等於0.216 23(表5)、0.322 688(表7)、0.053 72(表8),P(雙尾)分別等於0.432 459(表5)、0.645 376(表7)、0.107 44(表8)均大於0.05,所以,樣本數據組A1與A2、C1與C2、Dl與D2各兩組數據在統計學上沒有顯著性差異,即各兩組數據的均值在統計意義上是相等的。
考察表6中t檢驗的計量結果,P(單尾)等於2.53E-17(表6),P(雙尾)等於5.06E-17(表6),均小於0.05,所以樣本數據組B1與B2這兩組數據在統計學上具有顯著性差異,即各兩組數據的均值在統計意義上是不相等的。
三、結果解析
實證結果表明:(1)A1與A2不存在顯著性差異,即在同一時期發行的、期限結構完全相同的兩組企業債券,如果該兩組企業債券的債項評級和主體評級均相同,那麼其發行利差不存在顯著性差異。(2)B1與B2存在顯著性差異,即在同一時期發行的、期限結構完全相同的兩組企業債券,如果其中一組企業債券(B2)的債項評級和主體評級優於另一組(B1),則其發行利差存在顯著性差異。(3)C1與C2不存在顯著性差異,即在同一時期發行的、期限結構完全相同的兩組企業債券,如果該兩組企業債券的債項評級相同,主體評級不同,那麼其發行利差不存在顯著性差異。(4)Dl與D2不存在顯著性差異,即在同一時期發行的、期限結構完全相同的兩組企業債券,如果該兩組企業債券的主體評級相同,債項評級不同,則其發行利差不存在顯著性差異。
上述四項實證結果可進一步表述為:在其他條件相同時,只要信用評級相同(債項評級和/或主體評級相同),企業債券的發行利差(即發行成本)在統計學上不具有顯著性差異。在其他條件相同時,只要信用評級不同(債項評級和主體評級均不同),企業債券的發行利差(即發行成本)在統計學上也顯著不同。
據此,可以得出結論:(1)信用評級信息已經成為我國企業債券市場投資者制定投資決策的主要依據,市場投資者對信用評級信息有很強的依賴性。(2)信用評級信息在資本市場上對我國企業債券的市場定價具有顯著的影響力。(3)我國企業債券的市場定價是有效率的。
| rα α k | 0.10 0.05 0.02 0.01 0.001 | α rα k | ||||
|---|---|---|---|---|---|---|
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 25 30 35 40 45 50 60 70 80 90 100 | 0.9877 0.9000 0.8054 0.7293 0.6694 0.6215 0.5822 0.5494 0.5214 0.4973 0.4762 0.4575 0.4409 0.4259 0.4124 0.4000 0.3887 0.3783 0.3687 0.3598 0.3233 0.2960 0.2746 0.2573 0.2428 0.2306 0.2108 0.1954 0.1829 0.1726 0.1638 | 0.9969 0.9500 0.8783 0.8114 0.7545 0.7067 0.6664 0.6319 0.6021 0.5760 0.5529 0.5324 0.5139 0.4973 0.4821 0.4683 0.4555 0.4438 0.4329 0.4227 0.3809 0.3494 0.3246 0.3044 0.2875 0.2732 0.2500 0.2319 0.2172 0.2050 0.1946 | 0.9995 0.9800 0.9343 0.8822 0.8329 0.7887 0.7498 0.7155 0.6851 0.6581 0.6339 0.6120 0.5923 0.5742 0.5577 0.5425 0.5285 0.5155 0.5034 0.4921 0.4451 0.4093 0.3810 0.3578 0.3384 0.3218 0.2948 0.2737 0.2565 0.2422 0.2301 | 0.9999 0.9900 0.9587 0.9172 0.8745 0.8343 0.7977 0.7646 0.7348 0.7079 0.6835 0.6614 0.6411 0.6226 0.6055 0.5897 0.5751 0.5614 0.5487 0.5368 0.4869 0.4487 0.4182 0.3932 0.3721 0.3541 0.3248 0.3017 0.2830 0.2673 0.2540 | 0.9999 0.9990 0.9912 0.9741 0.9507 0.9249 0.8982 0.8721 0.8471 0.8233 0.8010 0.7800 0.7603 0.7420 0.7246 0.7084 0.6932 0.6787 0.6652 0.6524 0.5974 0.5541 0.5189 0.4896 0.4648 0.4433 0.4078 0.3799 0.3568 0.3375 0.3211 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 25 30 35 40 45 50 60 70 80 90 100 |
評論(共22條)
那什麼a b c 是什麼意思都沒說呀!?
請問樓上指的a b c在哪呀?
"4、在檢驗的操作中,把觀察到的顯著性水平與作為檢驗標準的顯著水平標準比較,小於這個標準時,得到了拒絕原假設的證據,認為樣本數據表明瞭真實差異存在。大於這個標準時,拒絕原假設的證據不足,認為樣本數據不足以表明真實差異存在。 "
沒看懂
遇到一個問題,雙邊檢驗H0下統計量值為0.48,服從標準正態分佈,p應該是2*(1-N(0.48))=0.63,非常大,表示無法拒絕原假設,但不代表能夠接受原假設吧?PS,無法拒絕H0就意味著原假設為真麽,不一定吧?
首先請恕我無知,我想請問一下那個顯著性標記是怎麼標上去的,有沒什麼規定,怎麼有些文獻是標的ab,有的是abcd,甚至有的是abcdef。。。原諒我沒有學過統計學。。
發生第二類錯誤的概率(記作 )是指,把來自\theta=\theta_1(\theta_1\ne\theta_0)的總體的樣本值代入檢驗統計量所得結果落入接受域的概率。
第二類錯誤概率的定義和計算一直是暈暈乎乎沒搞懂,麻煩詳細解釋一下,多謝








good job