假設檢驗
出自 MBA智库百科(https://wiki.mbalib.com/)
假設檢驗(Hypothesis Testing)
目錄 |
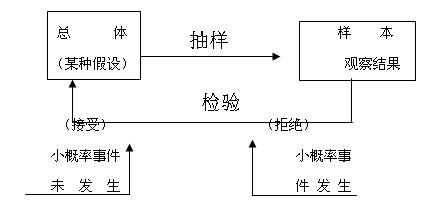
假設檢驗是用來判斷樣本與樣本,樣本與總體的差異是由抽樣誤差引起還是本質差別造成的統計推斷方法。其基本原理是先對總體的特征作出某種假設,然後通過抽樣研究的統計推理,對此假設應該被拒絕還是接受作出推斷。
生物現象的個體差異是客觀存在,以致抽樣誤差不可避免,所以我們不能僅憑個別樣本的值來下結論。當遇到兩個或幾個樣本均數(或率)、樣本均數(率)與已知總體均數(率)有大有小時,應當考慮到造成這種差別的原因有兩種可能:一是這兩個或幾個樣本均數(或率)來自同一總體,其差別僅僅由於抽樣誤差即偶然性所造成;二是這兩個或幾個樣本均數(或率)來自不同的總體,即其差別不僅由抽樣誤差造成,而主要是由實驗因素不同所引起的。假設檢驗的目的就在於排除抽樣誤差的影響,區分差別在統計上是否成立,並瞭解事件發生的概率。
在質量管理工作中經常遇到兩者進行比較的情況,如採購原材料的驗證,我們抽樣所得到的數據在目標值兩邊波動,有時波動很大,這時你如何進行判定這些原料是否達到了我們規定的要求呢?再例如,你先後做了兩批實驗,得到兩組數據,你想知道在這兩試實驗中合格率有無顯著變化,那怎麼做呢?這時你可以使用假設檢驗這種統計方法,來比較你的數據,它可以告訴你兩者是否相等,同時也可以告訴你,在你做出這樣的結論時,你所承擔的風險。假設檢驗的思想是,先假設兩者相等,即:μ=μ0,然後用統計的方法來計算驗證你的假設是否正確。
1.小概率原理
如果對總體的某種假設是真實的,那麼不利於或不能支持這一假設的事件A(小概率事件)在一次試驗中幾乎不可能發生的;要是在一次試驗中A竟然發生了,就有理由懷疑該假設的真實性,拒絕這一假設。
2.假設的形式
H0——原假設, H1——備擇假設
雙尾檢驗:H0:μ = μ0 ,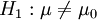
單尾檢驗: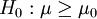 ,H1:μ < μ0
,H1:μ < μ0
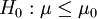 , H1:μ > μ0
假設檢驗就是根據樣本觀察結果對原假設(H0)進行檢驗,接受H0,就否定H1;拒絕H0,就接受H1。
, H1:μ > μ0
假設檢驗就是根據樣本觀察結果對原假設(H0)進行檢驗,接受H0,就否定H1;拒絕H0,就接受H1。
一般地說,對總體某項或某幾項作出假設,然後根據樣本對假設作出接受或拒絕的判斷,這種方法稱為假設檢驗。
假設檢驗使用了一種類似於“反證法”的推理方法,它的特點是:
(1)先假設總體某項假設成立,計算其會導致什麼結果產生。若導致不合理現象產生,則拒絕原先的假設。若並不導致不合理的現象產生,則不能拒絕原先假設,從而接受原先假設。
(2)它又不同於一般的反證法。所謂不合理現象產生,並非指形式邏輯上的絕對矛盾,而是基於小概率原理:概率很小的事件在一次試驗中幾乎是不可能發生的,若發生了,就是不合理的。至於怎樣才算是“小概率”呢?通常可將概率不超過0.05的事件稱為“小概率事件”,也可視具體情形而取0.1或0.01等。在假設檢驗中常記這個概率為α,稱為顯著性水平。而把原先設定的假設成為原假設,記作H0。把與H0相反的假設稱為備擇假設,它是原假設被拒絕時而應接受的假設,記作H1。
假設檢驗可分為正態分佈檢驗、正態總體均值分佈檢驗、非參數檢驗三類。
正態分佈檢驗包括三類:JB檢驗、KS檢驗、Lilliefors檢驗,用於檢驗樣本是否來自於一個正態分佈總體。
正態總體均值檢驗檢驗分析方法和分析結果的準確度,考察系統誤差對測試結果的影響。從統計意義上來說,各樣本均值之差應在隨機誤差允許的範圍之內。反之,如果不同樣本的均值之差超過了允許的範圍,這就說明除了隨機誤差之外,各均值之間還存在系統誤差,使得各均值之間出現了顯著性差異。
正態總體均值檢驗分為兩種情況,
t檢驗是用小樣本檢驗總體參數,特點是在均方差不知道的情況下,可以檢驗樣本平均數的顯著性,分為單側檢驗與雙側檢驗。當為雙樣本檢驗時,在兩樣本t檢驗中要用到F檢驗。
從兩研究總體中隨機抽取樣本,要對這兩個樣本進行比較的時候,首先要判斷兩總體方差是否相同,即方差齊性。若兩總體方差相等,則直接用t檢驗,若不等,可採用t'檢驗或變數變換或秩和檢驗等方法。
Z檢驗是一般用於大樣本(即樣本容量大於30)平均值差異性檢驗的方法。
上面所述的檢驗都是基於樣本來自正態總體的假設,在實際工作中,有時並不明確知道樣本是否來自正態總體,這就為假設檢驗帶來難度。非參數檢驗方法,對樣本是否來自正態總體不做嚴格的限制,而且計算簡單。統計工具箱提供了符號檢驗和秩和檢驗兩種非參數檢驗方法。
假設檢驗的基本思想是小概率反證法思想。小概率思想是指小概率事件(P<0.01或P<0.05)在一次試驗中基本上不會發生。反證法思想是先提出假設(檢驗假設H0),再用適當的統計方法確定假設成立的可能性大小,如可能性小,則認為假設不成立,若可能性大,則還不能認為假設不成立。
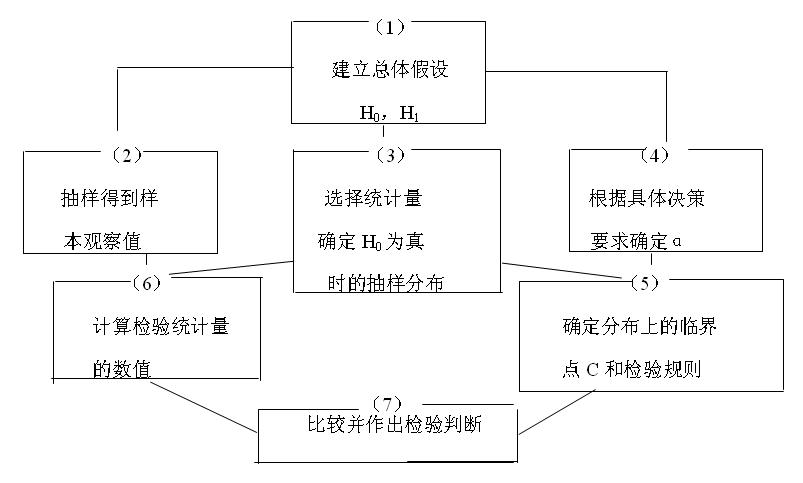
- 1.確定檢驗規則
檢驗過程是比較樣本觀察結果與總體假設的差異。差異顯著,超過了臨界點,拒絕H0;反之,差異不顯著,接受H0。
差異 臨界點 判斷 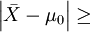
c 拒絕H0 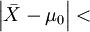
c 接受H0
怎樣確定c?
- 2.兩類錯誤
接受或拒絕H0,都可能犯錯誤
I類錯誤——棄真錯誤,發生的概率為α
II類錯誤——取偽錯誤,發生的概率為β
檢驗決策 H0為真 H0非真 拒絕H0 犯I類錯誤(α) 正確 接受H0 正確 犯II類錯誤(β)
α大β就小,α小β就大
基本原則:力求在控制α前提下減少β
α——顯著性水平,取值:0.1, 0.05, 0.001, 等。如果犯I類錯誤損失更大,為減少損失,α值取小;如果犯II類錯誤損失更大,α值取大。
確定α,就確定了臨界點c。
①設有總體:X~N(μ,σ2),σ2已知。
②隨機抽樣:樣本均值\bar{X}~N(\mu,\sigma^2/n)。
③ 標準化:
標準化: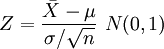
④確定α值,
⑤查概率表,知臨界值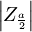
⑥計算Z值,作出判斷。
1、做假設檢驗之前,應註意資料本身是否有可比性。
2、當差別有統計學意義時應註意這樣的差別在實際應用中有無意義。
3、根據資料類型和特點選用正確的假設檢驗方法。
4、根據專業及經驗確定是選用單側檢驗還是雙側檢驗。
5、當檢驗結果為拒絕無效假設時,應註意有發生I類錯誤的可能性,即錯誤地拒絕了本身成立的H0,發生這種錯誤的可能性預先是知道的,即檢驗水準那麼大;當檢驗結果為不拒絕無效假設時,應註意有發生II類錯誤的可能性,即仍有可能錯誤地接受了本身就不成立的H0,發生這種錯誤的可能性預先是不知道的,但與樣本含量和I類錯誤的大小有關係。
6、判斷結論時不能絕對化,應註意無論接受或拒絕檢驗假設,都有判斷錯誤的可能性。
7、報告結論時是應註意說明所用的統計量,檢驗的單雙側及P值的確切範圍。
假設檢驗與置信區間有密切的聯繫,我們往往可以由某參數的顯著性水平為α的檢驗,得到該參數的置信度為1—α的置信區間,反之亦然。例如,顯著性水平α的均值μ的雙側檢驗問題:
H0:μ = μ0, 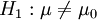
與置信度為1-α 的置信區間之間有著這樣的關係;若檢驗在α水平下接受H0,則μ的1 - α的置信區間必須包含μ0;反之,若檢驗在 α水平下拒絕H0,則μ的1-α的置信區間必定不包含μ0。因此,我們可以用構造μ的1-α置信區間的方法來檢驗上述假設,如果構造出來的置信區間包含μ0,就接受H0;如果不包含μ0就拒絕H0。同樣給定顯著水平 α,可以從構造檢驗規則的過程中,得到μ的 1-α置信區間。 如上例,μ的置信度為95%的置信區間為:
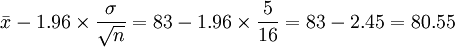
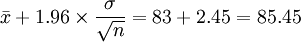
即置信區間為(80.55 , 85.45),因為μ0 = 80,不在這個區間內,拒絕H0
考慮下麵三種類型的假設檢驗: (4.12)
(1)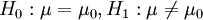 (雙邊檢驗)
(雙邊檢驗)
(2)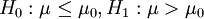 (右側單邊檢驗)
(右側單邊檢驗)
(3)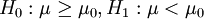 (左側單邊檢驗)
(左側單邊檢驗)
案例一:假設檢驗設備判斷中的應用[1]
例如:某公司想從國外引進一種自動加工裝置。這種裝置的工作溫度X服從正態分佈(μ,52),廠方說它的平均工作溫度是80度。從該裝置試運轉中隨機測試16次,得到的平均工作溫度是83度。該公司考慮,樣本結果與廠方所說的是否有顯著差異?廠方的說法是否可以接受?
類似這種根據樣本觀測值來判斷一個有關總體的假設是否成立的問題,就是假設檢驗的問題。我們把任一關於單體分佈的假設,統稱為統計假設,簡稱假設。上例中,可以提出兩個假設:一個稱為原假設或零假設,記為H0:μ=80(度);另一個稱為備擇假設或對立假設,記為H1 :μ≠80(度)這樣,上述假設檢驗問題可以表示為:
H0:μ=80 H1:μ≠80
原假設與備擇假設相互對立,兩者有且只有一個正確,備擇假設的含義是,一旦否定原假設H0,備擇假設H1備你選擇。所謂假設檢驗問題就是要判斷原假設H0是否正確,決定接受還是拒絕原假設,若拒絕原假設,就接受備擇假設。
應該如何作出判斷呢?如果樣本測定的結果是100度甚至更高(或很低),我們從直觀上能感到原假設可疑而否定它,因為原假設是真實時,在一次試驗中出現了與80度相距甚遠的小概率事件幾乎是不可能的,而現在竟然出現了,當然要拒絕原假設H0。現在的問題是樣本平均工作溫度為83度,結果雖然與廠方說的80度有差異,但樣本具有隨機性,80度與83度之間的差異很可能是樣本的隨機性造成的。在這種情況下,要對原假設作出接受還是拒絕的抉擇,就必鬚根據研究的問題和決策條件,對樣本值與原假設的差異進行分析。若有充分理由認為這種差異並非是由偶然的隨機因素造成的,也即認為差異是顯著的,才能拒絕原假設,否則就不能拒絕原假設。假設檢驗實質上是對原假設是否正確進行檢驗,因此,檢驗過程中要使原假設得到維護,使之不輕易被否定,否定原假設必須有充分的理由;同時,當原假設被接受時,也只能認為否定它的根據不充分,而不是認為它絕對正確。
案例二:假設檢驗在卷煙質量判斷中的應用[2]
在卷煙生產企業經常會遇到如下的問題:卷煙檢驗標準中要求煙支的某項缺陷的不合格品率P不能超過3%,現從一批產品中隨機抽取50支卷煙進行檢驗,發現有2支不合格品,問此批產品能否放行?按照一般的習慣性思維:50支中有2支不合格品,不合格品率就是4%,超過了原來設置的3%的不合格品率,因此不能放行。但如果根據假設檢驗的理論,在α=0.05的顯著性水平下,該批產品應該可以放行。這是為什麼呢?
最關鍵的是由於我們是在一批產品中進行抽樣檢驗,用抽樣樣本的質量水平來判別整批的質量水平,這裡就有一個抽樣風險的問題。舉例來說,我們的這批產品共有10000支卷煙,裡面有4支不合格品,不合格品率是0.04%,遠低於3%的合格放行不合格品率。但我們的檢驗要求是隨機抽樣50支,用這50支的質量水平來判別整批 10000支的質量水平。如果在50支中恰好抽到了2支甚至更多的不合格品,簡單地用抽到的不合格品數除以50來作為不合格品率來判斷,那我們就會對這批質量水平合格的產品進行誤判。
如何科學地進行判斷呢?這就要用到假設檢驗的理論。
步驟1:建立假設
要檢驗的假設是不合格品率P是否不超過3%,因此立假設
H0:P≤0.03
這是原假設,其意是:與檢驗標準一致。
H1:P>0.03
步驟2:選擇檢驗統計量,給出拒絕域的形式
若把比例P看作n=1的二項分別b(1,p)中成功的概率,則可在大樣本場合(一般n≥25)獲得參數p的近似μ的檢驗,可得樣本統計量: 近似服從N(0,1)
其中=2/50=0.04,p=0.03,n=50
步驟3:給出顯著性水平α,常取α=0.05。
步驟4:定出臨界值,寫出拒絕域W。
根據α=0.05及備擇假設知道拒絕域W為
步驟5:由樣本觀測值,求得樣本統計量,並判斷。
結論:在α=0.05時,樣本觀測值未落在拒絕域,所以不能拒絕原假設,應允許這批產品出廠。
假設檢驗中的兩類錯誤。
進一步研究一下這個例子,在50個樣品中抽到多少個不合格品,就要拒絕入庫呢?我們仍取α=0.05,根據上述公式,得出,解得x>3.48,也就是在50個樣品中抽到4個不合格品才能判整批為不合格。
而如果我們改變α的取值,也就是我們定義的小概率的取值,比如說取α=0.01,認為概率不超過0.01的事件發生了就是不合理的了,那又會怎樣呢?還是用上面的公式計算,則得出,解得x>4.30,也就是在50個樣品中抽到5個不合格品才能判整批為不合格。檢驗要求是不合格品率P不能超過3%,而現在根據α=0.01,算出來50個樣品中抽到5個不合格品才能判整批為不合格,會不會犯錯誤啊!假設檢驗是根據樣本的情況作的統計推斷,是推斷就會犯錯誤,我們的任務是控制犯錯誤的概率。在假設檢驗中,錯誤有兩類:
第一類錯誤(拒真錯誤):原假設H0為真(批產品質量是合格的),但由於抽樣的隨機性(抽到過多的不合格品),樣本落在拒絕域W內,從而導致拒絕H0(根據樣本的情況把批質量判斷為不合格)。其發生的概率記為α,也就是顯著性水平。α控制的其實是生產方的風險,控制的是生產方所承擔的批質量合格而不被接受的風險。
第二類錯誤(取偽錯誤):原假設H0不真(批產品質量是不合格的),但由於抽樣的隨機性(抽到過少的不合格品),樣本落在W外,從而導致接受H0(根據樣本的情況把批質量判斷為合格)。其發生的概率記為β。β控制的其實是使用方的風險,控制的是使用方所承擔的接受質量不合格批的風險。
再回到剛剛計算的上例的情況,α由0.05變化為0.01,我們對批質量不合格的判斷由50 個樣本中出現4個不合格變化為5個,批質量是合格的而不被接受的風險就小了,犯第一類錯誤的風險小了,也就是生產方的風險小了;但同時隨著α的減小對批質量不合格的判斷條件其實放寬了——50個樣本中出現4個不合格變化為5個,批質量是不合格的而被接受的風險大了;犯第二類錯誤的風險大了,也就是使用方的風險大了。 在相同樣本量下,要使α小,必導致β大;要使β小,必導致α大,要同時兼顧生產方和使用方的風險是不可能的。要使α、β皆小,只有增大樣本量,這又增加了質量成本。
因此綜上所述,假設檢驗可以告訴我們如何科學地進行質量合格判定,又告訴我們要兼顧生產方和使用方的質量風險,同時考慮質量和成本的問題。
- ↑ 俞良蒂.統計學原理.第四章 參數估值與假設檢驗.中國地質大學(武漢)
- ↑ 孫厲.假設檢驗在卷煙質量判斷中的應用
評論(共24條)
請問,大樣本和小樣本的界限是25還是30呀?還是不同的書有不同的規矩??大樣本和小樣本的假設檢驗會一樣嗎?
一切隨緣。
請問,大樣本和小樣本的界限是25還是30呀?還是不同的書有不同的規矩??大樣本和小樣本的假設檢驗會一樣嗎?
30
請問,假設檢驗與置信區間的關係 μ的置信度為95%的置信區間為:
中1.96的是怎麼來的 拜托拜托,上帝保佑你
查表
thx終於明白到底怎麼設定原假設了:1、問:是否明顯A事件,原假設就定為非A事件,充分否定了非A,才能保證明顯A。2、問:是否A事件,原假設就定為A事件,不能充分否定A事件就說明A事件可能會發生。因為是基於小概率事件的反證,這兩個解裡面,如果α<0.5,問題1中A事件的變數取值域要小於問題2中A事件的變數的取值域,而差的這部分域剛好是變數以1-2α為置信水平的置信區間。而當α為0.5時,可以發現,這兩個部分不會有差別了,那就可以換個思路了:不會存在明顯和可能的差別了,某事件發生一次就說明瞭它發生了(因為發生與不發生是等概率的,不存在小概率這一稱呼了)。當α>0.5時,顯然這裡的變數已經本來該小概率的事件變成了正常的,而正常的變成了小概率事件了,反過來理解就行了,不過這樣α也失去了意義,畢竟其取值一般在0.05,0.025,0.01等。 回過來看,問題1可能發生變數的棄真,問題2可能會發生取偽(這也剛好說明瞭為什麼問題1的變數取值域要小於問題2的變數取值域,棄的真和取的偽都集中在置信區間內)所以如果A事件為煙捲可以放行,1問題也就是明顯可以放行,2問題也就是可以放行,這樣就能和文中的對接上了。
thx終於明白到底怎麼設定原假設了:1、問:是否明顯A事件,原假設就定為非A事件,充分否定了非A,才能保證明顯A。2、問:是否A事件,原假設就定為A事件,不能充分否定A事件就說明A事件可能會發生。因為是基於小概率事件的反證,這兩個解裡面,如果α<0.5,問題1中A事件的變數取值域要小於問題2中A事件的變數的取值域,而差的這部分域剛好是變數以1-2α為置信水平的置信區間。而當α為0.5時,可以發現,這兩個部分不會有差別了,那就可以換個思路了:不會存在明顯和可能的差別了,某事件發生一次就說明瞭它發生了(因為發生與不發生是等概率的,不存在小概率這一稱呼了)。當α>0.5時,顯然這裡的變數已經本來該小概率的事件變成了正常的,而正常的變成了小概率事件了,反過來理解就行了,不過這樣α也失去了意義,畢竟其取值一般在0.05,0.025,0.01等。 回過來看,問題1可能發生變數的棄真,問題2可能會發生取偽(這也剛好說明瞭為什麼問題1的變數取值域要小於問題2的變數取值域,棄的真和取的偽都集中在置信區間內)所以如果A事件為煙捲可以放行,1問題也就是明顯可以放行,2問題也就是可以放行,這樣就能和文中的對接上了。
說的好!!!









very good!