秩和檢驗

出自 MBA智库百科(https://wiki.mbalib.com/)

秩和檢驗（Rank sum test）

　　秩和檢驗方法最早是由維爾克松提出，叫維爾克松兩樣本檢驗法。後來曼—惠特尼將其應用到兩樣本容量不等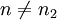（）的情況，因而又稱為曼—惠特尼U檢驗。這種方法主要用於比較兩個獨立樣本的差異。

　　1、假設中的等價問題

　　設有兩個連續型總體, 它們的概率密度函數分別為：

　　f₁(x),f₂(x)(均為未知)

　　已知f₁(x) = f₂(x − a)，a為末知常數，要檢驗的各假設為：

H₀:A = 0,H₁:a < 0.

H₀:A = 0,H₁:a > 0.

.

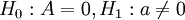　　設兩個總體的均值存在，分別記為μ₁,μ₂，由於f₁,f₂最多只差一平移，則有μ₂ = μ₁ − a。此時, 上述各假設分別等價於：

H₀:μ₁ = μ₂,H₁:μ₁ < μ₂

H₀:μ₁ = μ₂,H₁:μ₁ > μ₂

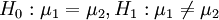
　　2、秩的定義

　　設X為一總體，將容量為n的樣本觀察值按自小到大的次序編號排列成x₍₁₎ < x₍₂₎ < Λ < x_(n),稱x_(i)的足標i為x_(i)的秩，i = 1,2,Λ,n。

　　例如：某施行團人員的行李重量數據如表：

　　寫出重量33的秩。

　　因為28<33<34<39<41，故33的秩為2。

　　特殊情況：

　　如果在排列大小時出現了相同大小的觀察值, 則其秩的定義為足標的平均值。

　　例如: 抽得的樣本觀察值按次序排成0,1,1,1,2,3,3,

則3個1的秩均為,

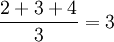兩個3的秩均為.

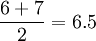　　3、秩和的定義

　　現設1，2兩總體分別抽取容量為n₁,n₂的樣本，且設兩樣本獨立。這裡總假定。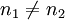

　　我們將這n₁ + n₂個觀察值放在一起，按自小到大的次序排列，求出每個觀察值的秩，然後將屬於第1個總體的樣本觀察值的秩相加，其和記為R₁，稱為第1樣本的秩和，其餘觀察值的秩的總和記作R₂，稱為第2樣本的秩和。

　　顯然，R₁和R₂是離散型隨機變數，且有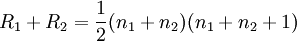

　　4、秩和檢驗法的定義

　　秩和檢驗是一種非參數檢驗法, 它是一種用樣本秩來代替樣本值的檢驗法。

　　用秩和檢驗可以檢驗兩個總體的分佈函數是否相等的問題

　　如果兩個樣本來自兩個獨立的但非正態或形態不清的兩總體，要檢驗兩樣本之間的差異是否顯著，不應運用參數檢驗中的T檢驗，而需採用秩和檢驗。

　　1、兩個樣本的容量均小於10的檢驗方法

　　檢驗的具體步驟：

　　第一步：將兩個樣本數據混合併由小到大進行等級排列（最小的數據秩次編為1，最大的數據秩次編為n₁ + n₂）。

　　第二步：把容量較小的樣本中各數據的等級相加，即秩和，用T表示。

　　第三步：把T值與秩和檢驗表中某α顯著性水平下的臨界值相比較，如果T₁ < T < T₂，則兩樣本差異不顯著；如果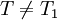或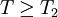，則表明兩樣本差異顯著。

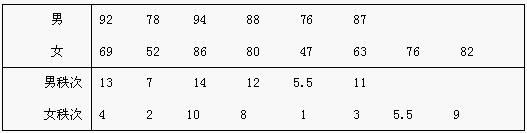
　　例：某年級隨機抽取6名男生和8名女生的英語考試成績如表1所示。問該年級男女生的英語成績是否存在顯著差異？

　　　　　　　　 男、女生英語考試成績表

　　解：檢驗步驟：

　　（1）建立假設：

H₀：男女生的英語成績不存在顯著差異

H₁：男女生的英語成績存在顯著差異

　　（2）編排秩次，求秩和：

　　T= 13 + 7 + 14 + 12 + 5.5 + 11= 62.5

　　（3）統計推斷：根據n₁ = 6,n₂ = 8,α = 0.05， 查秩和檢驗表，T的上、下限分別為T₁ = 29,T₂ = 61，有T > T₂，結論是：男女生的英語成績存在顯著差異。

　　3、兩個樣本的容量均大於10的檢驗方法

　　當兩個樣本容量都大於10時，秩和T的分佈接近於正態分佈，因此可以用Z檢驗，其基本公式為：

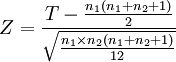
　　式中：T為較小的樣本的秩和。

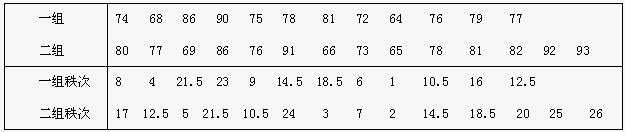
　　例:某校演講比賽後隨即抽出兩組學生的比賽成績如表2，問兩組成績是否有顯著差異？

　　解：檢驗步驟：

　　（1）建立假設：

H₀：兩組成績不存在顯著差異

H₁：兩組成績存在顯著差異

　　（2）編排秩次，求秩和：

n₁ = 12,n₂ = 14,T = 144.5，代入公式，有：

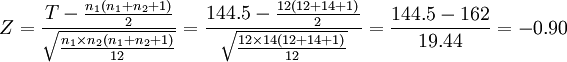
　　（3）統計推斷：因為|Z|<1.96，則應保留虛無假設，拒絕備擇假設。結論是：兩組的演講比賽成績不存在顯著差異。